含变质量构件的轴向运动梁的横向振动主动控制

马驰骋　张希农　代祥俊　周长城　郭宗和

摘要： 轴向运动结构是一类广泛使用的工程传送元件，而在传送过程中常常包含质量运动或者质量变化，质量的运动或改变和轴向运动间相互耦合作用，使结构的振动更加突出。为满足轴向运动机构高精度准定位的需求，围绕含变质量构件的机械臂结构，开展变质量-轴向运动耦合作用结构的振动主动控制研究。首先基于Galerkin法和模态叠加法建立了变质量-轴向运动压电梁的控制方程，然后针对系统的时变特性，设计LQG控制器对系统进行振动主动控制，并分析了多种工况下结构的振动抑制问题，最后采用Choi-Williams分布将信号在时频域上分解，分析了控制前后系统的时频特性。数值分析表明，施加LQG控制后，系统的横向振动在相关频率内都得到了有效的抑制，使用Choi-Williams分布可以准确反映系统振动频率与振动能量随时间的变化规律。通过研究含时变参数的轴向运动结构的运动特性和振动主动控制，对于智能机械臂结构设计具有一定指导意义。

关键词： 振动主动控制; 轴向运动梁; 变质量; LQG控制器

中图分类号： TB 535  文献标志码： A  文章编号： 1004-4523（2019）03-0396-08

DOI：10.16385/j.cnki.issn.1004-4523.2019.03.003

引 言

柔性机械臂结构在工程搬运或者传输等行业极大程度上替代了人力劳动，有效提高了质量传输效率。然而构件的轴向运动或者物品质量的变化都会引起结构整体参数的改变，关于含变质量构件的轴向运动结构的动力学问题研究，开展的相对较晚，而在各类交通工具，车桥耦合系统，空天大型柔性结构和荷载机械臂等实际工程问题中，又迫切地需要开展变质量-轴向运动系统的动力学响应及其振动主被动控制方面的科学研究。

Marynowski等详细总结了轴向运动结构的研究进展，随着工业自动化的普及，有关轴向运动结构动力学问题的研究近年来迅速增多[1]。Ghayesh等[2]为解决时变速度轴向运动梁的非线性动力学问题，在计算中综合使用了Galerkin法、模态叠加法和伪弧长法，FFT变换等技术，对分析轴向运动结构提供了一种参考。Yang等[3]针对轴向运动梁的横向与纵向耦合振动，基于 Galerkin法推导了系统的运动方程，通过调整速度参数，得到了系统振动能量传递规律，结果表明耦合振动的能量转移可以用来实现结构的振动控制。吕海炜等[4]提出了一种全新的夹层梁理论，用于建立轴向运动软夹层梁横向振动控制方程，比传统轴向运动夹层梁模型的应用范围更广，更有普适性。考虑梁的剪切变形的影响，陈红永等[5]研究了轴向运动Timoshenko梁在轴向载荷作用下的振动特性，探索了影响临界速度和临界载荷的因素，对于轴向受载运动系统设计具有一定指导意义。刘金建等[6]重点研究了轴向运动黏弹性梁横向振动的稳定性问题，分析了轴向匀速运动中功能梯度黏弹性梁亚临界区域内横向振动的复频率随轴向运动速度、材料梯度指数等参数的变化情况。

从上述轴向运动结构动力学问题的研究中发现，轴向运动会显著影响机械臂结构的操作精度和运动稳定性，采用主动控制来提高结构的运动精度是一项迫切而可行的工作。张伟等针对轴向运动弦线和作动器组成的耦合系统的横向振动控制，采用自适应方法[7]和Lyapunov方法[8]，均对该类系统的振动进行了有效的控制。He等[9]则对有输出约束的运动弦系统进行了振动控制研究。刘定强等[10]利用有限差分法，采用二次最优控制和速度反馈法分析轴向运动矩形薄膜横向振动的控制问题，并给出了最优控制律。王亮等[11-12]提出主动振子和主动力两种方法，有效地控制了轴向运动速度、变长度悬臂梁的横向振动。在某些机器人系统运动中，构件除了有轴向运动，还会有绕轴转动。Zhao[13]等采用一种自感应作动器对安装有转动关节的轴向运动机器臂开展了振动主动控制，有效地降低了轴向运动机械臂的振动幅值。在天然气石油开采中，钻井隔水系统普遍面临着变长度变张力以及变速度等问题，He[14]等采用一种边界控制策略实现了某钻井隔水系统的振动抑制。

针对含变质量构件的轴向运动梁，本文主要开展了时变参数系统的动力学响应分析及振动主动控制两个方面的工作，具体内容如下：首先推导了变质量-轴向运动压电梁结构的运动方程，研究了该类系统的振动特性;然后采用LQG控制器对质量增大和质量减少两类工况下的轴向运动结构进行了振动控制;最后探索了基于Choi-Williams分布函数的时频分析技术在时变参数系统振动控制中的应用。

2 动力学特性分析

仿真中梁结构的结构阻尼比值分别取1%和0.05%。当梁长度不变时，系统简化为含末端变质量的悬臂梁结构，梁末端的位移响应曲线如图3所示。梁结构初始长度1.8 m，m（t）从0增大到2 kg，或者从2 kg减少到0。虽然梁长度不改变，但是从图3中仍可以看出，末端质量减小时，振动频率增大，同时位移幅值逐渐增大;而质量增大时，振动频率降低，同时位移幅值逐渐减小。这是由于质量变化引起的一个非结构阻尼项，该非结构阻尼项与系统的质量变化率成正比，当<0时，质量变化引起一个非结构负阻尼，使得系统的振幅增大;反之，>0时，系统质量增大相当于引起一个正阻尼，使得系统振幅加速衰减。

当末端质量不变时，系统简化为含集中质量的轴向运动梁。梁長度的改变会同时引起系统刚度和质量的变化，轴向运动梁末端的响应如图4所示，伸长时系统的频率降低，同时振幅增大，随轴向移动速度增加，从0.05 m/s到0.15 m/s再到0.25 m/s，梁的横向振动位移幅值增大的更快，而缩短时随轴向移动速度增加，梁的横向振动位移幅值衰减加速。

当既有质量变化，又有轴向运动时，一方面需要考虑轴向运动对系统的影响;另一方面也要考虑质量变化对系统的影响，系统的运动规律更加复杂。含变质量构件的轴向缩短梁的末端位移响应如图5（a）所示，末端质量增大引起的非结构正阻尼使梁的横向振动幅值衰减更加迅速;末端质量减小时，附加负阻尼会减慢振动的衰减。伸长时梁末端的响应如图5（b）所示，减小末端质量，附加负阻尼使梁的横向振动幅值增加更加明显;末端质量增大时，质量变化引起的附加正阻尼会削弱轴向伸长引起的振幅增大。含变质量参数的轴向运动梁的运动规律如表3所示，只有当v>0，<0和v<0，>0时，才能直接判断系统幅值的改变规律，但是与之相关的频率信息又无法直接确定，这些因素都增加了振动控制的困难度和复杂性。

3 LQG控制器

对于含变质量的轴向运动结构，系统内质量参数、刚度参数和阻尼参数都随时间变化，传统的控制方法如PID反馈控制，难以保证时变参数系统全局控制的稳定性[16]，LQG控制法是一种稳定而且适用性广的控制策略，通过选择评价指标的加权系数，实现最优控制，控制流程图如图6所示。

4 振动控制

在薄壁结构的振动中，主要以低阶模态为主，因此主动控制的中心思想是尽可能消耗低阶振动能量。针对变质量-轴向运动梁的自由振动，给定结构一个初始位移，与梁的一阶模态接近，释放位移約束后，结构开始振动，然后通过LQG控制器，调控压电片实现梁的振动抑制。

首先考虑梁伸长（v=0.1 m/s）的情况，质量增大和质量减少两种工况下系统的位移响应如图7所示。对比控制前后的位移响应，可以明显看出施加LQG控制后，结构的振动幅值迅速衰减，说明了LQG策略对时变参数系统控制的有效性。而且从图7（b）中可以发现，位移幅值随时间逐渐增大，这说明系统质量减小引起的非结构负阻尼作用十分显著，因此在结构动力学分析中，质量变化引起的非结构阻尼效应不可忽略，尤其是质量减少的系统。

类似的，梁缩短（v=-0.1 m/s），末端质量变化时系统的位移响应如图8所示，运动过程中梁的长度从1.8 m缩短到0.8 m。从图中可以发现施加控制后，结构的振动得到有效的抑制。对比图8（a）和（b）中未控制时系统的响应曲线，也表明系统质量变化引起的非结构阻尼作用会很大程度上影响系统的振动特性。

5 时频响应分析

在变质量系统的振动信号处理中，使用Fourier变换虽然可以得到系统的频域特征，但是无法得到系统共振频率和振动能量的时变特性[17-18]。为了更全面地分析时变参数系统的非稳态响应信号，科研工作者运用了多种时频分布函数，如Wigner-Ville分布，短时傅里叶变换（STFT），Choi-Williams分布（Choi Williams Distribution，简称CWD）等[17]，这些分布函数被广泛应用于机械设计、振动监测和故障诊断等领域。相比较Wigner-Ville分布等技术，Choi-Williams分布函数采用固定核函数滤波，具有良好的信号分辨率和时频聚集性，可以有效抑制多个频率信号分量共存时的交叉项干扰，使能量在时频域上的分布更加密集，因此本文采用Choi-Williams分布函数来分析处理控制前后的非平稳响应信号。

对图7（a）中的位移响应曲线做CWD，得到了图9中显示的控制前后系统位移曲线的时频响应谱。梁结构从1.8 m伸长至2.8 m， 同时系统的质量从0增加到2 kg，从图9中可以看出系统的振动频率从2.37 Hz降低到0.75 Hz，同时可以发现系统的振动能量随时间迅速减少，也就是说施加控制后，系统的振动得到了有效控制。对于质量减少的情况，时频响应谱图如图10所示：系统的振动频率从1.65 Hz降低到0.98 Hz，从图10（a）可以看出，系统的振动能量随时间增加，这是非结构负阻尼起了重要的作用。

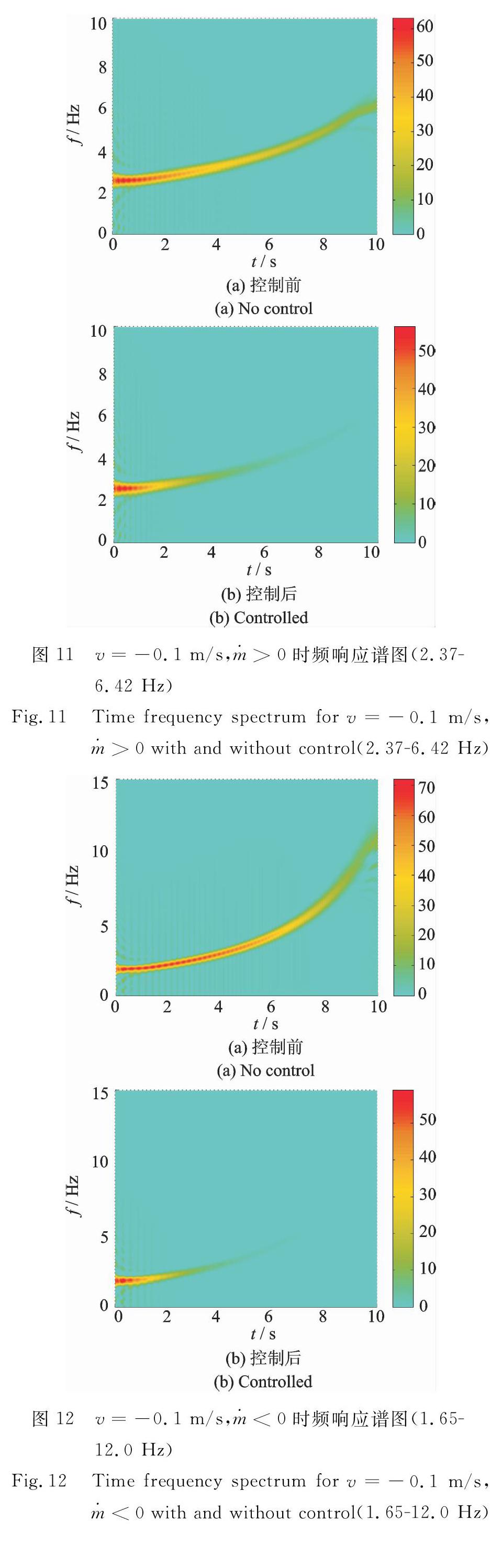
同样的，对图8中的位移响应做CWD，可以得到图11和12中显示的梁缩短时，质量增大工况和质量减少工况时的时频响应谱。梁结构从1.8 m缩短至0.8 m，系统质量从0增加到2 kg时，从图11，12中可以看出系统振动频率从2.37 Hz增大到6.42 Hz;而当系统质量从2 kg减少到0时，系统的振动频率从1.6 Hz增大到12 Hz。对比图11和12，施加控制后，振动能量迅速减小，说明通过LQG控制器对时变参数系统开展振动控制是可行的。

综上所述，借助时频分析技术，可以得到系统振动频率随时间的变化规律和系统振动能量的变化谱图，这是传统FFT 变换无法得到的。对于质量时变系统，系统没有固定振动频率，而是以时变振动频率形式存在，但是系统振动频率的范围可以通过系统质量的变化范围确定， 这也是时变系统与时不变系统差别最大的地方。在某些工作环境中，系统所受外激励力的作用频率可能恰好在系统的振动频率变化范围内，这时候需要在限定的频率范围内开展主动控制，而通过时频分析技术，可以得到频率与时间的对应关系，为时变参数系统的振动控制提供参考。

6 结 论

通过对变质量-轴向运动梁的振动特性分析和主动控制研究，得到以下结论：

1） 质量变化使系统振动频率变化的同时，会引起一个非结构阻尼，该非结构阻尼正比于系统的质量变化率。质量增加，质量变化率大于零，非结构阻尼为正阻尼;系统质量减少，质量变化率小于零，非结构阻尼为负阻尼，负阻尼可能引起系统振动幅值的增大和系统振动的不稳定。

2） 使用LQG控制器对变质量-梁组合结构的自由振动系统的振动控制效果显著，在时变的频率范围内，结构的振动都得到了有效的抑制。

3） 通过响应信号的时频分析，可以得到系统的振动频率随时间的变化规律和振动能量的时频响应谱。根据时频分析，便于在指定时间指定频率对系统的振动进行抑制。

参考文献：

[1] Marynowski K， Kapitaniak T. Dynamics of axially moving continua[J]. International Journal of Mechanical Sciences， 2014， 81： 26-41.

[2] Ghayesh M H， Amabili M. Steady-state transverse response of an axially moving beam with time-dependent axial speed[J]. International Journal of Non-Linear Mechanics， 2013， 49： 40-49.

[3] Yang X D， Zhang W. Nonlinear dynamics of axially moving beam with coupled longitudinal transversal vibrations[J]. Nonlinear Dynamics， 2014， 78（4）： 2547-2556.

[4] 吕海炜，李映辉，李 亮，等. 軸向运动软夹层梁横向振动分析[J]. 振动与冲击， 2014，33（02）： 41-46.

Lv Haiwei， Li Yinghui， Li Liang et al. Analysis of transverse vibration of axially moving soft sandwich beam[J]. Journal of Vibration and Shock， 2014，33（02）： 41-46.

[5] 陈红永，李上明. 轴向运动梁在轴向载荷作用下的动力学特性研究[J]. 振动与冲击， 2016， 35（19）： 75-80.

Chen Hongyong， Li Shangming. Dynamic characteristics of an axially moving Timoshenko beam under axial loads[J]. Journal of Vibration and Shock， 2016， 35（19）： 75-80.

[6] 刘金建，蔡改改，谢 锋，等. 轴向运动功能梯度黏弹性梁横向振动的稳定性分析[J]. 动力学与控制学报， 2016，14（06）： 533-541.

Liu Jinjian， Cai Gaigai， Xie Feng， et al. Stability anslysis on transverse vibration of axially moving functionally graded viscoelastic beams[J]. Journal of Dynamics and Control， 2016， 14（06）： 533-541.

[7] 张 伟，陈立群. 轴向运动弦线横向振动控制的自适应方法[J]. 机械工程学报， 2006， 42 （04）： 96-100.

Zhang Wei， Chen Liqun. Transverse vibration control of an axially moving string system by adaptive method[J]. Chinese Journal of Mechanical Engineering， 2006， 42（04）： 96-100.

[8] 张 伟，陈立群. 轴向运动弦线横向振动控制的Lyapunov方法[J]. 控制理论与应用， 2006， 23（04）： 531-535.

Zhang Wei， Chen Liqun. Transverse vibration control of an axially moving string system by Lyapunov method[J]. Control Theory & Applications， 2006， 23（04）： 531-535.

[9] He W， Ge S S， Huang D. Modeling and vibration control for a nonlinear moving string with output constraint[J]. IEEE/ASME Transactions on Mechatronics， 2015， 20（4）： 1886-1897.

[10] 刘定强，王忠民. 轴向运动矩形薄膜的横向振动控制[J]. 西安理工大学学报， 2007， 23（01）： 62-65.

Liu Dingqiang， Wang Zhongmin. The transverse vibration control of an axially moving rectangular membrane[J]. Journal of Xi′an University of Technology， 2007， 23（01）： 62-65.

[11] 王 亮，陈怀海，贺旭东，等. 轴向运动变长度悬臂梁的振动控制[J].振动工程学报，2009，22（06）：565-570.

Wang Liang， Chen Huaihai， He Xudong， et al. Vibration control of an axially moving cantilever beam with varying length[J]. Journal of Vibration Engineering， 2009， 22（06）： 565-570.

[12] 王 亮，陈怀海，贺旭东，等. 轴向运动悬臂梁横向振动的磁力控制[J]. 南京航空航天大学学报， 2010， 42（05）： 568-573.

Wang Liang， Chen Huaihai， He Xudong， et al. Active vibration control of axially moving cantilever beam by magnetic force[J]. Journal of Nanjing University of Aeronautics & Astronautics， 2010， 42（05）： 568-573.

[13] Zhao L， Hu Z D. Active vibration control of an axially translating robot arm with rotating prismatic joint using self-sensing actuator[J]. Shock and Vibration， 2015，2015：964139.

[14] He W， Nie S， Meng T， et al. Modeling and vibration control for a moving beam with application in a drilling riser [J]. IEEE Transactions on Control Systems Technology， 2017， 25（3）： 1036-1043.

[15] Meirovitch L. Dynamics and Control of Structures[M]. New York：Wiley， 1990.

[16] Gawronski W K. Advanced Structural Dynamics and Active Control of Structures[M]. New York： Springer， 2004

[17] Cohen L. Time frequency distributions-review[J]. Proceedings of the IEEE， 1989， 77（7）： 941-981.

[18] 姜 鳴， 陈 进， 汪慰军. 几种Cohen类时频分布的比较及应用[J]. 机械工程学报， 2003， 29（3）： 129-134.

Abstract： Axially moving structures are widely used as basic components in kinds of delivery systems. It is very common that mass changing or mass moving occurs in the process of delivery， which causes the increase or decrease of the total mass. The coupling of variation of the mass and the axially moving makes more significant vibration of the structures. This paper studies the active vibration control of the axially moving structures with time varying mass by taking an axially moving manipulator attached with a time varying concentrated mass as a specific subject. The governing equations of the time varying system are derived using Galerkin method and mode superposition method. Then LQG controller is designed for controlling the vibration of the system with different conditions taken into account， including the increasing mass system and the decreasing mass system. Finally， the response signals are decomposed by the method of Choi Williams distribution， and the time frequency features are obtained. Numerical simulations demonstrate that the vibration of the system is effectively controlled under the LQG controller in the limited range of frequencies， and the variation of the frequency and vibration energy can be given by Choi Williams distribution， showing that it is a much more powerful tool than FFT. The study on the dynamic characteristics and active control of the axially moving structures with time varying mass can offer guides to innovative design of smart manipulators.

Key words： active vibration control; axially moving beam; variable mass; LQG