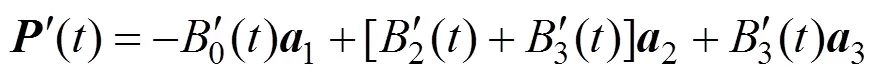一类三角Bézier曲线的形状特征

吴荣军

一类三角Bézier曲线的形状特征

吴荣军

(西安邮电大学理学院，陕西 西安 710121)

在几何造型的许多应用中，良好的曲线形状应该消除不必要的奇点和拐点，因此往往需要预知与分析参数曲线的各种形状特征，以避免出现奇异形状的设计风险。为了快速确定参数曲线的形状特征，利用锥面的齐次性简化了参数曲线的形状条件，得出了一类带2个形状参数的二次三角Bézier曲线的尖点条件锥和2张重结点边界条件锥；3张特征锥面及其切平面将特征空间划分为不同的特征区域。曲线的形状特征完全由特征点在特征空间的分布区域决定。用垂直于坐标轴的平面切割特征空间，可得到基于包络与拓扑映射方法的所有形状条件分布图。进而讨论了形状参数变化对各特征区域的影响，相关结果可使设计者明确如何配置控制顶点或者调节形状参数，使得生成曲线为全局凸或局部凸曲线，或具有所需要的奇点与拐点，或将当前曲线形状调节为另一种所需的形状。

三角Bézier曲线；形状特征；尖点锥；重结点锥

参数曲线的形状特征，主要指曲线的奇点、拐点及凸性。其几何特征的判定条件对于参数曲线的形状控制与调节具有重要作用。与之密切相关的主要研究有仿射不变量方法[1]、基于包络和拓扑映射的方法[2]和基于控制顶点轨迹的几何刻画方法[3]。形状分析法[4-6]对基于包络和拓扑映射的方法做了补充，在相应的形状条件分布图中区分出了全局凸和局部凸区域。3种方法对曲线形状特征的分析都需要假设某2个边向量是不平行的，实际上，文献[3]在仿射不变量方法提出后，就曾设想能否去掉平行假设，但也没有解决这一问题；特征空间方法[7]得出了一系列造型曲线的形状特征判断条件，其判断不需要平行假设。本文讨论一类带形状参数的二次三角多项式Bézier曲线[8-9]的形状特征，得出的特征空间与已有的Bézier型曲线[7]的特征空间结构类似，不同之处在于，其尖点锥的切平面方程含有形状参数，从而使得该曲线形状参数的调节能力优于诸多带形状参数的Bézier型曲线[7]。

1 三角带参Bézier曲线简介

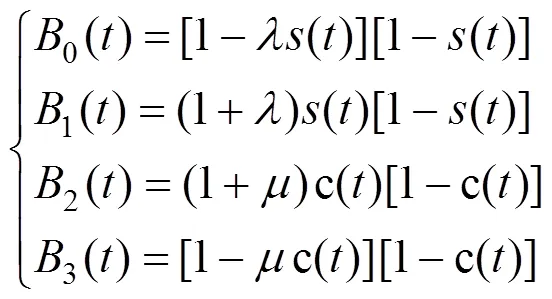
2 尖点条件锥

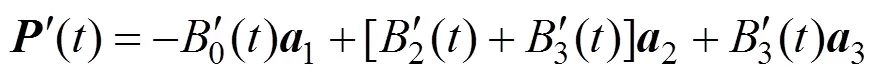
实际上，由及还可分别得到形式的尖点条件线

《失业保险条例》规定的失业保险保障对象为城镇企业事业单位职工，京津冀一体化背景下河北省城镇化步伐不断加快，而新生代农民工成为城市职工当中的一员，然而，高失业率的新生代农民工对政策了解甚少，出现“应保未保”、“待遇水平低”以及“跨区转移困难”等问题，加深了农民工群体的就业困境。因此，建立长效机制的农民工失业保险政策应重视农民工需求，保障农民工的权益，能有效为农民工解决后顾之忧，不但让其“进得来”，还要“留得下”。新型城镇化不仅是户籍的城镇化，更重要的是让农民工与城镇居民同等享有国家政策，给新生代农民工落户城镇提供更多的机会。

及

如果将、及看作三维空间的点，那么分别以3点为末端，以原点(0,0,0)为起点所构成的向量是相互平行的，并且都与经过点

(2) 和原点的直线平行。受该性质启发，构造以这些直线为母线的锥面，由式(2)消去参数t可得到锥面方程，，y，c2<0或00，那么用–d作为新的特征点进行判断即可，从而可使特征点位置的判断大为简化(以下讨论仅限于下半空间)。 对高速公路桥梁进行养护这样的工作对专业度有要求，公路桥梁出现问题，并不是只要能够把损毁给弥补就可以了，还要考虑到多个方面的问题，比如如何使用最低的成本来保证养护的质量，如何让公路桥梁的养护工作带来的影响降到最低等等，这些都需要专业的养护人员来解决。 6.4 形状参数对特征空间的影响 首先，因为重结点边界锥的切平面的方程式不含形状参数，所以形状参数变化不影响全局凸区域(如图6左下区域所示)；从而可知，当曲线的控制多边形为全局凸[6]时，无论如何调节形状参数，曲线始终保持全局凸。 (a) λ=μ=1 (b) λ=μ=0.5 (c) λ=μ=–0.5 图6 形状参数变化对特征空间的影响 如图6所示，改变形状参数，可对3张特征锥面及切平面ci进行调节。注意到切平面c1与切平面π2的交线为x轴，当参数减小时，切平面c1与π2的夹角随之减小，当时，c1的极限位置就是π2；类似的有，切平面c2与切平面π1的交线为轴，当参数减小时，切平面c2与π2的夹角随之减小，当时，c2的极限位置就是π1。当时，尖点锥Fc的极限位置为切平面π1与π2，重结点边界锥F1的极限位置为切平面π2，重结点边界锥F2的极限位置为切平面π1。所以随着形状参数(或)减小，重结点区域L、双拐点区域I2以及局部凸区域相应缩小；全局凸区域N01及单拐点区域相应扩大。 本文所得曲线的特征空间，与已有Bézier型曲线[7]的特征空间结构类似，除了具体方程外，最大不同之处在于，通过形状参数调节尖点锥在边界处的切平面c1和c2，可对双拐点区域I2及重结点区域L进行压缩。 图7(a)~(c)对应的控制顶点为b0=[0,0]T， b1=[2,2]T，b2=[0,2]T，b3=[1,1.5]T；相应曲线形状变化说明，当控制多边形是局部凸[6]时，改变形状参数可以将曲线形状调节为局部凸。 图7(d)~(i)中对应的控制顶点为b0=[0,0]T，b1=[2,2]T，b2=[0,2]T，b3=[2,0]T；相应曲线形状变化说明，当控制多边形的首末2边相交时，通过修改形状参数可以将曲线的形状调节为全局凸；图7(d)~(i)的变化显示了同时减小形状参数及时，切平面对区域的压缩，使得特征点属于全局凸区域N01 (如图6所示)。 (a) 尖点(λ≠μ)(b) 重结点(端点)(c) 局部凸 (d) 重结点(内部)(e) 尖点(λ=μ)(f) 2个拐点 (g) 1个拐点(区域S2)(h) 1个拐点(区域S1)(i) 全局凸 图7 三角Bézier曲线的形状特征 而已有的诸多Bézier型曲线[7]都不具备这种调节能力，因为其尖点锥的2张切平面分别是及(如图6(a)所示)。图7(g)~(h)说明当控制多边形的首末2边相交时，可通过调节形状参数使得特征点属于单拐点区域S1 (图7(h))或S2 (图7(g))。图7中的各曲线的特征判断见表1 (其中特征点的计算利用了6.3的简化性质)。 上述讨论表明，当特征点属于切平面c1与π2 (或者切平面c2与π1)所围成区域内部时，可通过形状参数对曲线P(t)的形状特征进行一定程度的调节，特征点越靠近切平面πi，形状参数的调节能力越强，曲线可选择的形状特征越多。 第五个支出是社会保障支出，关于社会保障支出的主要有以下几个问题：社会保障支出总量不足；社会保障支出增长缓慢；社会保障支出结构不合理、地区差异显著；社会保障基金增值困难、安全隐患。这个具体的数据大概说一下：2010年的时候我们国家社会保障支出占GDP的2.28%。这个与同期国家比较，比如说以中等发达国家为例，中等发达国家社会保障支出比重是30%，我们是2.28%，社会保障构建上严重投入不足，今天我们所讲的全民享有的、能够覆盖13亿人口的社会保障体系尚未完全建立起来。 表1 图7中相关曲线的特征判断 序号特征点形状参数区域判断特征区域 (a)(–1,–3,–4)λ=0.4927554, μ=1Fc=0尖点锥 (b)(–1,–3,–4)λ=0.9609671, μ=1F2=0重结点区域 (c)(–1,–3,–4)λ=1, μ=0.25F2<0, π1>0局部凸区域 (d)(–4,–8,–4)λ=1, μ=1Fc<0, F1>0, F2>0重结点区域 (e)(–4,–8,–4)λ=0.707107, μ=0.707107Fc=0尖点锥 (f)(–4,–8,–4)λ=0.25, μ=0.25Fc>0, c1<0, c2<0双拐点区域 (g)(–4,–8,–4)λ=–0.25, μ=0.25c1<0, c2>0单拐点区域 (h)(–4,–8,–4)λ=0.25, μ=–0.25c1>0, c2<0单拐点区域 (i)(–4,–8,–4)λ=–0.25, μ=–0.25c1>0, c2>0全局凸区域 7 结束语 本文讨论了带2个形状参数的二次三角多项式Bézier曲线的形状特征判断问题，得到了该曲线的特征空间，各特征区域由尖点锥和重结点边界锥及其切平面对三维空间划分而成，特征点由控制多边形边向量对应的二阶行列式构成，区域判断只涉及特征点关于锥面及平面的代入计算，因而非常适合于计算机程序自动判断；并进一步分析了形状参数对特征锥及其切平面的调节作用。 参考文献 [1] SU B Q, LIU D Y. An affine invariant theory and its application in computational geometry [J]. Scientia Sinica，Series A, 1983, 26(3): 259-272. [2] 叶正麟. 一类平面B-样条曲线的形状分类[J]. 纯粹数学与应用数学, 1990, 6(1): 72-74. [3] STONE M C, DEROSE T D. A geometric characterization of parametric cubic curves [J]. ACM Transactions on Graphics, 1989, 8(3): 147-163. [4] 吴荣军, 叶正麟, 罗卫民. 有理C-Bézier曲线的形状分析[J]. 计算机学报, 2007, 30(11): 2055-2059. [5] 吴荣军. 平面三次H-Bézier曲线的形状分析[J]. 应用数学学报, 2007, 30(5): 816-821. [6] 吴荣军, 彭国华, 罗卫民, 等. 四次带参Bézier曲线的形状分析[J]. 计算机辅助设计与图形学学报, 2009, 21(6): 725-729. [7] 吴荣军. 参数曲线形状分析的特征空间方法研究[D]. 西安: 西北工业大学, 2015. [8] HAN X L. Quadratic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2002, 19(7): 503-512. [9] 吴晓勤, 韩旭里, 罗善明. 带形状参数的二次三角Bézier曲线[J]. 工程图学学报, 2008, 29(1): 82-87. [10] 徐迎博, 喻德生. 带形状参数的二次三角多项式Bézier曲线形状分析[J]. 浙江大学学报:理学版, 2013, 40(1): 35-41. Shape Features of a Kind of Trigonometric Bézier Curve WU Rong-jun (School of Science, Xi’an University of Posts and Telecommunications, Xi’an Shaanxi 710121, China) Abstract: In many applications of geometric modeling, curves of desirable shape should eliminate the unnecessary singularities and inflection points. Therefore, to avoid potential risk in shape design, it is essential to predict and analyze the shape features of parametric curves. In order to quickly determine the shape features of parametric curves, the shape conditions of the parametric curve are simplified due to the homogeneous property of cones, and the cusp conditional cone and two boundary loop conditional cones are obtained for a quadratic trigonometric polynomial Bézier curve characterized with two shape parameters. These three characteristic cones and their tangent planes divide the characteristic space into different characteristic regions. The curve's shape features are completely determined by the distribution region which the characteristic point locates in the characteristic space. It is shown that the shape diagrams obtained by the method based on the theory of envelopes and topological mappings can be derived from characteristic space by virtue of planar slices, which are vertical to one of the axes. Furthermore, the influences of shape parameters on the associated characteristic regions are also discussed. The obtained results enable the user to place control points or choose shape parameters so that the resulting curve is globally or locally convex, possessing wanted singularities or inflection points, or enjoying the desired shape features. Keywords: trigonometric Bézier curves; shape features; cusp cones; loop cones 中图分类号：TP 391 DOI：10.11996/JG.j.2095-302X.2019030549 文献标识码：A 文章编号：2095-302X(2019)03-0549-07 收稿日期：2018-11-15； 定稿日期：2018-12-18 基金项目：陕西省教育厅专项科研项目(14JK1655)；陕西省自然科学基础研究计划项目(2018JM1054) 第一作者：吴荣军(1975-)，男，陕西白水人，讲师，博士。主要研究方向为计算机辅助几何设计、数值分析等。E-mail：wrj2140@163.com