‘海沃德’猕猴桃应力松弛特性与品质关系

卢丹，赵武奇，曾祥媛，吴妮，高贵田，张清安，张宝善，雷玉山

（1陕西师范大学食品工程与营养科学学院，西安 710119；2陕西省农村科技开发中心，西安 710119）

0 引言

【研究意义】我国是世界上猕猴桃栽培和出口的主要国家之一，猕猴桃酸甜可口，富含多种营养成分，有“水果之王”的美誉，更受大家青睐[1]。猕猴桃的营养价值和质地是评价其品质的主要指标，是猕猴桃贮藏及分级的重要依据。传统的猕猴桃品质检测方法为化学检测法，对果实进行破坏性检测，存在操作复杂、耗时较长[2]的缺点，因此，探求一种快速、方便地检测猕猴桃品质的方法是目前研究的热点之一。食品流变学是研究物料物质形态和流动的学科。猕猴桃作为一种黏弹性物料具有显著的流变特性，因此，利用其流变学特性来研究猕猴桃品质变化具有重大意义。【前人研究进展】食品流变学是研究食品或食品原料在力作用下变形或流动的科学。食品的弹性力学和黏性流体力学可以反映食品本身内部的化学成分、分子构造及食品的品质。RYSZARD等[3]运用应力松弛试验将猪肉与禽肉的化学成分与流变特性联系起来，得到的流变模型可用于加工肉制品的优化生产。SILVINA等[4]运用应力松弛试验区分低脂鸡肉肠的不同配方。聂毓琴等[5]研究野生富硒植物薇菜茎的应力松弛，证明薇菜茎具有良好的黏性和弹性的力学特性，是一种良好的黏弹性物料。ZHAO等[6]对苹果的应力模型参数与苹果品质的相关性进行分析，为苹果的贮藏奠定了基础。王海鸥等[7]通过压缩-应力松弛研究了猕猴桃各部位组织的流变特性参数，为猕猴桃的流变特性和品质分析奠定了基础。计宏伟等[8]通过绘制猕猴桃蠕变-时间曲线，为猕猴桃的加工及贮藏提供了力学依据。研究表明，食品的应力松弛特性能反映其品质，可用于食品的贮藏和加工。【本研究切入点】目前为止，应用应力松弛对果品的研究已有报道，但大部分仅限于对于单一品质的研究，未对果品的大部分品质指标进行全面的分析；对于猕猴桃的应力松弛研究仅限于研究猕猴桃内部的组织结构或内部的力学特性，很少将猕猴桃的应力松弛特性和其品质联系起来，并实现对猕猴桃品质的预测。【拟解决的关键问题】本试验以不同贮藏时期的猕猴桃为样本，对猕猴桃进行应力松弛试验，运用因子分析方法筛选出猕猴桃的品质特征指标，对猕猴桃应力松弛模型参数与其品质特征进行相关性分析，建立数学模型并对猕猴桃品质特征进行预测。

1 材料与方法

1.1 材料

‘海沃德’猕猴桃于2017年10月中旬采摘自陕西佰瑞猕猴桃研究院有限公司果园，样品采收及贮藏符合 NY/T 1392—2015《猕猴桃采收及贮运技术规范》，避免雨天和雨后采收，采收过程中严防机械损伤，轻采轻放，除去小果、烂果、病虫果、畸形果等，将猕猴桃样品装入纸箱中置于温度为（0±0.5）℃，相对湿度为90%—95%的冷库中。

1.2 试验仪器

TA.XT plus 质构仪，英国Stable Micro Systems公司；BA224S电子天平，北京赛多利斯仪器系统有限公司；8101手持糖量计，辽宁大连先超科技有限公司；CR-400/401型色彩色差仪，德国；UV-1800型紫外分光光度计，日本岛津公司；高速冷冻离心机，Thermo公司。

1.3 试验方法

在猕猴桃贮藏期间，每3 d随机抽取3个果实样品作为一组试验对象，将测试结果取平均值，共抽取50次，150个果样。每次试验前将果样置于20℃条件下静置1 h，然后依次进行应力试验、质构剖面感官分析法（texture profile analysis，TPA）试验和营养成分测试。从50组样品中随机抽取35组样本用于猕猴桃品质预测模型的构建，其余15组作为验证样本，用于预测模型的验证。

1.3.1 猕猴桃应变特性测试 应力测试参数为：探头P/5（直径5 mm），变形量0.5 mm，松弛时间50 s，加载速度1.0 mm·s-1，触发力0.049 N，数据采集频率10点/s。被测试样品呈水平放置，用底座固定。每个样品在最大横截面处取3个点进行测试，结果取平均值。

1.3.2 猕猴桃应力松弛模型确定 麦克斯韦模型描述的是黏弹性物料的应力松弛情况，由胡克模型和阻尼模型串联而成。广义麦克斯韦模型是由多个麦克斯韦（Maxwell）模型并联而成[9]。在试验过程中，随着压缩过程的进行，猕猴桃的受力面积会发生变化，得到一条力—时间曲线来分析猕猴桃的应力松弛行为。将力—时间曲线与Maxwell模型进行拟合，所用的拟合公式如下：

麦克斯韦三元件模型：

F(t)=D0E0+D0E1exp(-t/T1)

麦克斯韦五元件模型：

F(t)=D0E0+D0E1exp(-t/T1)+D0E2exp(-t/T2)

麦克斯韦七元件模型：

F(t)=D0E0+D0E1exp(-t/T1)+D0E2exp(-t/T2)+D0E3exp(-t/T3)

式中，F(t)为物料所受载荷（N），D0为恒定的应变量，E0是平衡弹性模量（N·mm-1），E1、E2和E3为弹性系数（N·mm-1）；T1、T2和T3是模型元件的松弛时间，t是松弛时间（s）。

ηi=EiTi

η为模型的黏性系数（N·S·mm-1），分别将 1.3.1测得的数据进行拟合，确定最佳模型。

1.3.3 品质指标测定 可溶性固形物（soluble solids，SS）用手持糖量计进行测定，每个果实取果汁测定，然后取该组果实测定值的平均值；可滴定酸用 NaOH标准溶液滴定，参见GB/T 12456—2008《食品中总酸的测定方法》，猕猴桃中可滴定酸以柠檬酸计；Vc用 2, 6-二氯靛酚染料溶液滴定，参见 GB 5009.86—2016《水果、蔬菜Vc含量测定法》。色差用CR-400/401型色彩色差仪直接测定a*、b*、L*值；丙二醛（MDA）含量的测定采用硫代巴比妥酸比色法，以mmol·g-1FW表示；每项指标测试3次，取平均值。

TPA测试：用取样器取直径为1 cm、厚度为0.5 cm的圆柱形猕猴桃果柱，在测前速度为4 mm·s-1，测中速度为2 mm·s-1，测后速度为4 mm·s-1，位移1 mm，时间5 s，触发力5 g的条件下进行TPA测试，每项指标测试3次，取平均值。

1.4 数据统计分析

采用Origin8.0软件对应力试验数据与1.3.2确定的应力模型进行拟合，得到应力模型的参数；用SPSS软件进行因子分析、相关性分析和岭回归分析；应用DPS7.5软件对应力模型参数进行误差分析和显著性t检验。

2 结果

2.1 猕猴桃品质指标测定结果

表1为50个猕猴桃理化指标与质构指标统计结果，由表1可知，可滴定酸、Vc、可溶性固形物、丙二醛及穿刺硬度的变化范围分別为 1.33%—2.69%、23.56—85.10 mg·kg-1FW、10.3%—15.30%、0.74—10.42 µmol·g-1、2.00—10.78；色差 L*值、a*值、b*值及ΔE的变化范围分别为25.97—45.98、-5.50—-1.34、0.01—11.71、26.12—47.60；质构指标硬度、粘附度、弹性、黏聚性、胶黏性、咀嚼性和回弹性的变化范围分别为 67.70—1067.05 N、-47.08—-3.29 N、0.75—1.30 N·s、0.64—0.92、62.06—775.51、58.50—757.53、0.21—0.39。从变异系数可以看出各项理化指标和质构指标离散性较大，说明选取的50组样本十分丰富，可以充分反映猕猴桃保藏过程中各项理化指标和质构指标的变化。

2.2 因子分析

对猕猴桃的可滴定酸、VC、可溶性固形物、丙二醛、穿刺硬度、色差L*值、a*值、b*值、ΔE、硬度、粘附度、弹性、黏聚性、胶黏性、咀嚼性和回弹性这16个指标进行因子分析，得到猕猴桃品质的特征值及方差贡献率、因子分析碎石图和正态方差最大正交旋转变换后的因子载荷矩阵，结果分别如表2、图1和表3所示。

由表2可知，因子分析所提出的5个主因子的特征值分别为4.412、3.372、1.794、1.580和1.227，方差贡献率分别为27.576%、21.077%、11.214%、9.877%和7.670%。所提出的5个主因子特征值均大于1，且累计方差贡献率达到77.41%，说明这5个主因子所构成的要素包括了 16个猕猴桃品质指标的绝大部分信息。因此，可以将猕猴桃的16个品质指标压缩为5个。

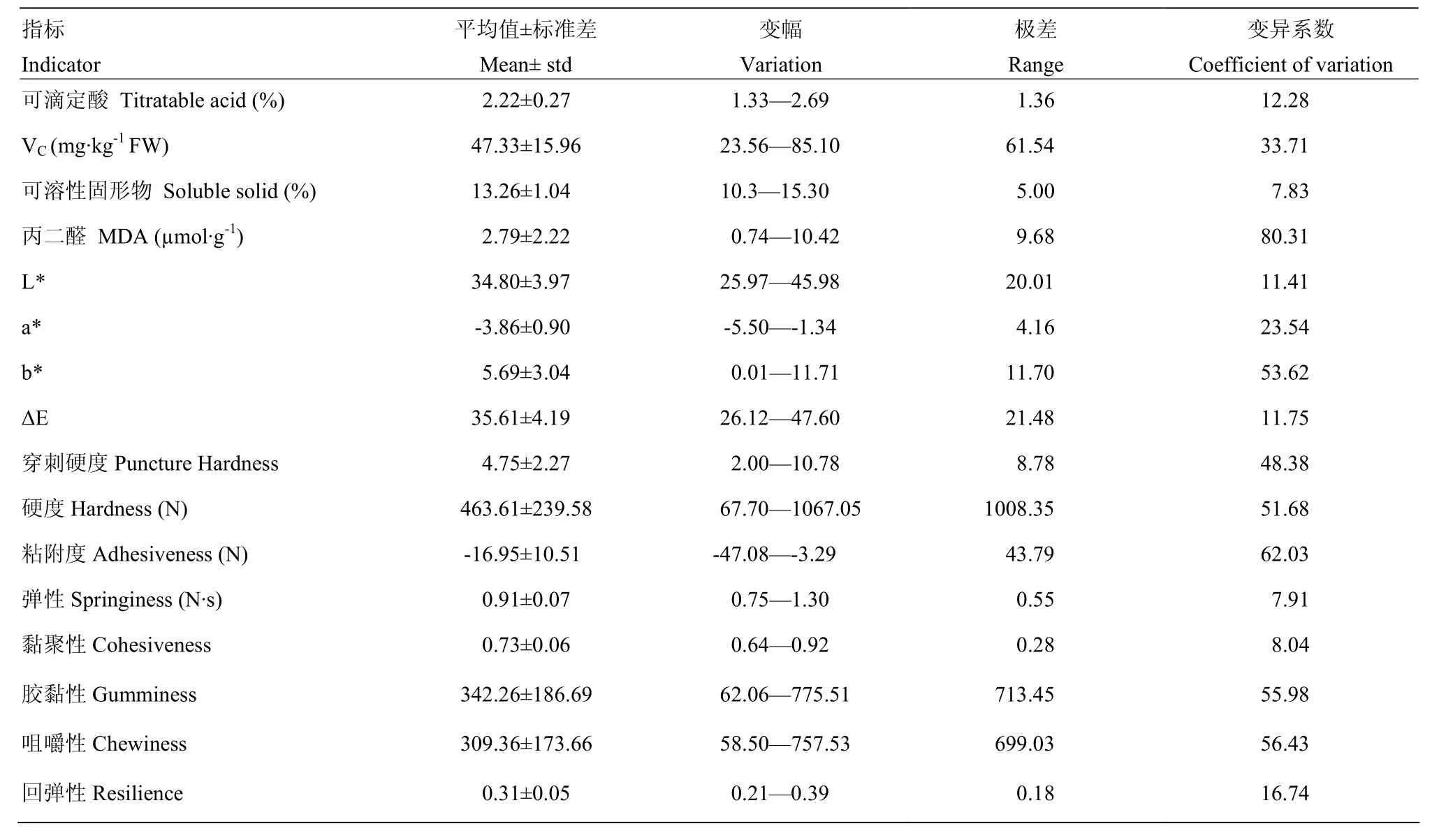
表1 猕猴桃品质指标的变异情况Table1 Variation of quality indexes of kiwifruit

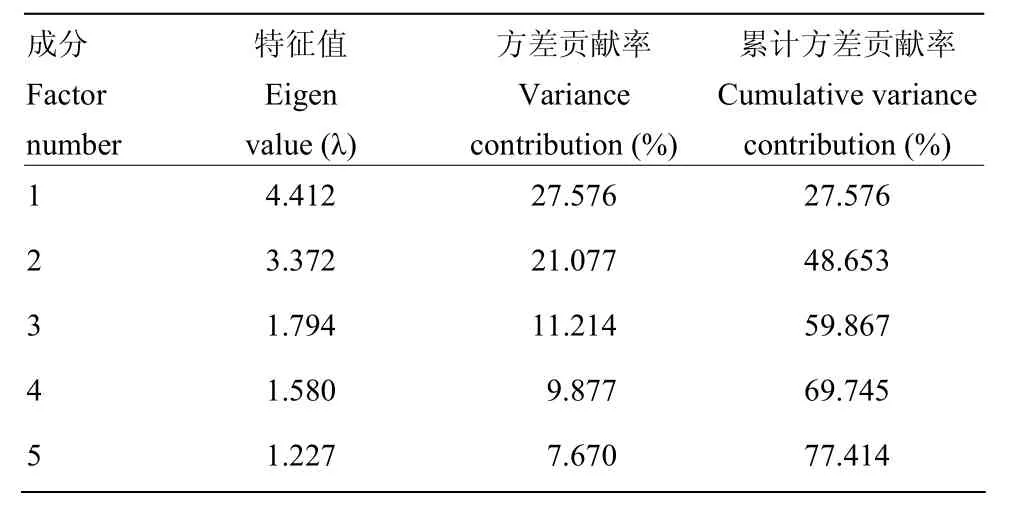
表2 因子分析解释总变量Table2 Total variance explained of factor analysis

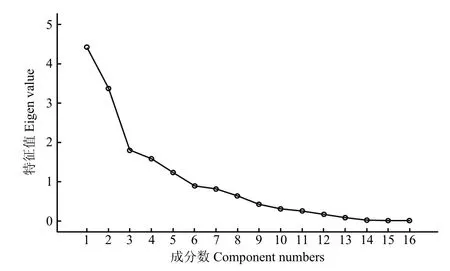
图1 因子分析碎石图Fig.1 Screen plot of factor analysis

图1为因子分析碎石图，由图1可以直观地看出从第 5个因子往后，曲线变得平缓，斜率越来越小，说明从第 5个因子往后各主因子的方差贡献率越来越小，所以提5个主因子是合适的。

采用方差极大化方法进行因子旋转，得到旋转后的因子载荷矩阵表3，旋转后，载荷大小进一步分化，因子与变量之间的对应关系更加清晰，每一个变量对于因子的影响程度也更加直观[10-11]。如表3所示，第1个主成分中，硬度、胶黏性、咀嚼性和黏附度4个指标为主变量，体现了猕猴桃的质构指标；第2个主成分中，ΔE、L*值、a*值、b*值4个指标为主变量，体现了猕猴桃的色泽指标；第3个主成分中，黏聚性、回弹性和可滴定酸3个指标为主变量，体现了猕猴桃的质构和化学指标；第四个主成分中，弹性、穿刺硬度和VC3个指标为主变量，体现了猕猴桃的质构和化学指标；第五个主成分中，可溶性固形物和丙二醛两个指标为主变量，可分别作为该主因子的代表性指标。以每个主因子中载荷最大为标准，可筛选出硬度、ΔE、黏聚性、弹性和可溶性固形物5个指标，但考虑到VC是猕猴桃中最主要的营养成分且其载荷大于0.55，则最终选取 VC、可溶性固形物、ΔE、硬度、黏聚性、弹性6个指标为猕猴桃的品质特征指标。

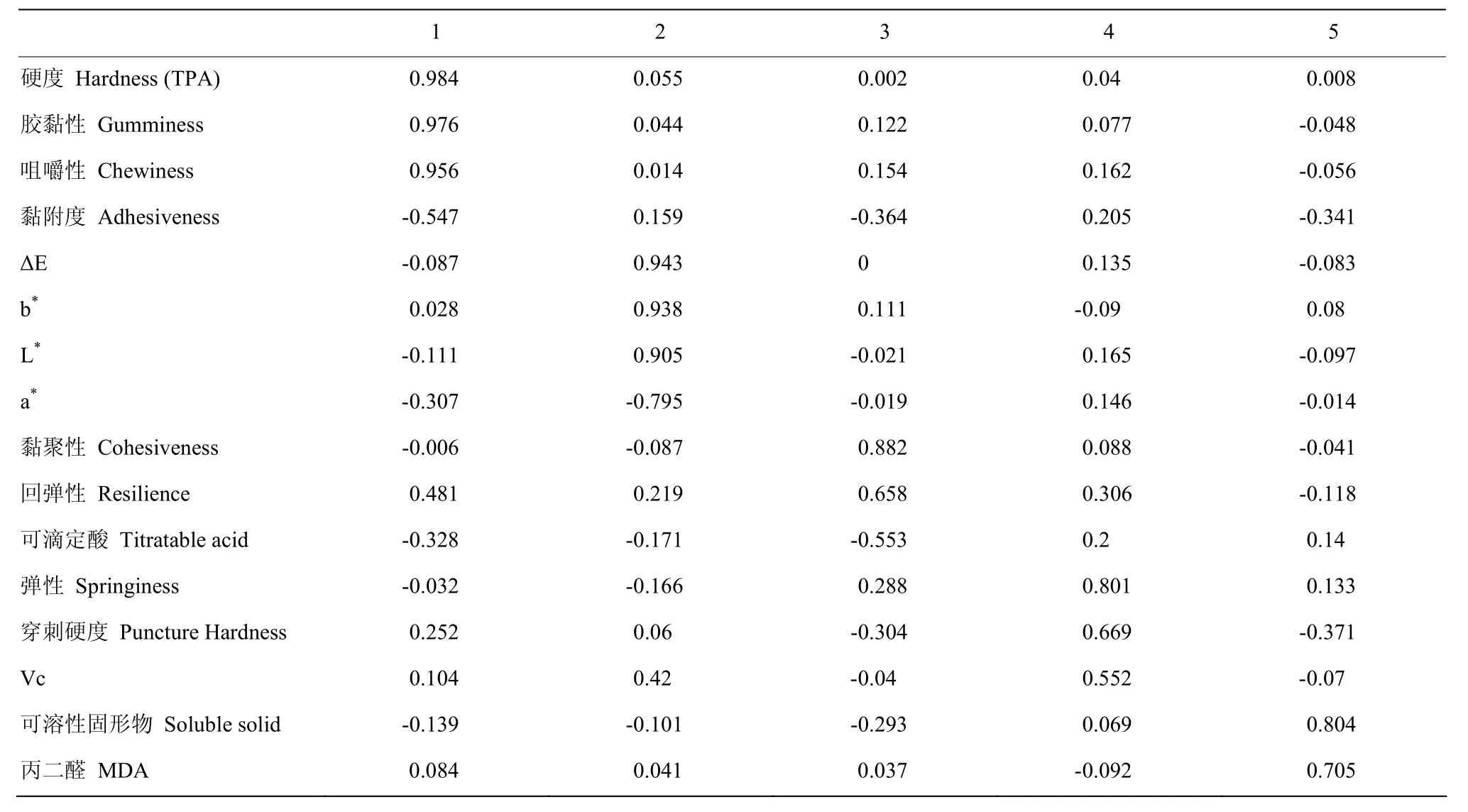
表3 猕猴桃品质正态方差最大正交旋转变换后的因子载荷矩阵Table3 Matrix of kiwifruit quality with normal variance after maximum orthogonal rotational transformation

2.3 应力松驰模型的确定

表4为50个样本数据分别与三元件麦克斯韦模型、五元件麦克斯韦模型和七元件麦克斯韦模型拟合得到的拟合结果。由表4可知，七元件麦克斯韦模型R2均值高于三元件麦克斯韦模型和五元件麦克斯韦模型，变异系数低于三元件麦克斯韦模型和五元件麦克斯韦模型，说明七元件麦克斯韦模型拟合效果最好。七元件麦克斯韦模型包括弹性参数（E0、E1、E2和E3）、松弛时间（T1、T2和T3）和黏性系数（η1、η2和 η3）。

表4 应力模型拟合结果Table4 Fitting results of stress model

2.4 应力松驰模型参数的确定

表5为应变模型参数统计结果，可以看出，建模组中平衡弹性系数 E0的变异系数最大，松弛时间 T2的变异系数最小，说明随着猕猴桃的贮藏，E0的变化最明显，松弛时间T2的变化最小。另外，所选的验证组的数据范围全都包括在建模组的范围内，说明验证组及建模组的划分是合理的。从变异系数来看，各个应力松弛参数的数值均较高，说明贮藏过程中的猕猴桃样本丰富且样本数据有效。

将应力模型的各个参数进行相关性分析，由表6中的皮尔森相关系数可知，弹性参数之间、松弛时间之间和黏性系数之间均存在很强的相关性，其中 E0与E3的相关系数为0.993、T2与T3之间为-0.753，η2与η3之间为0.983，松弛时间之间互为负相关；弹性参数与黏性参数之间相关性均极显著，其中E0与η2、η3之间相关系数分别为 0.983、0.998，E3与 η2、η3之间相关系数分别为 0.985、0.991；松弛时间与黏性系数和弹性参数之间的相关性系数均不高，仅 T2与E2、T3与E2之间相关性极显著，相关系数分别为-0.510和0.520；T1与η1相关性显著，相关系数为0.356。

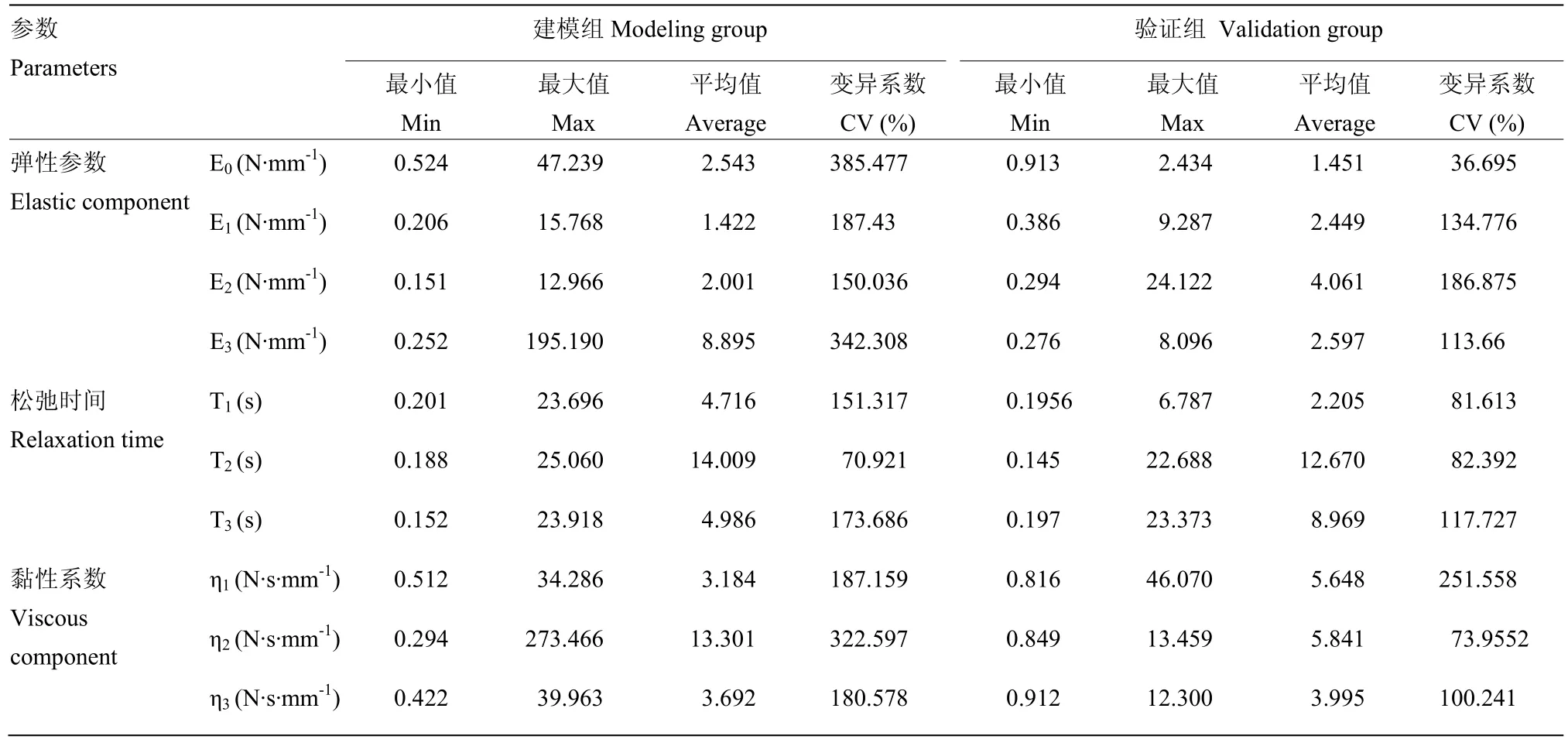
表5 应变模型参数统计结果Table5 Statistical results of strain model parameters

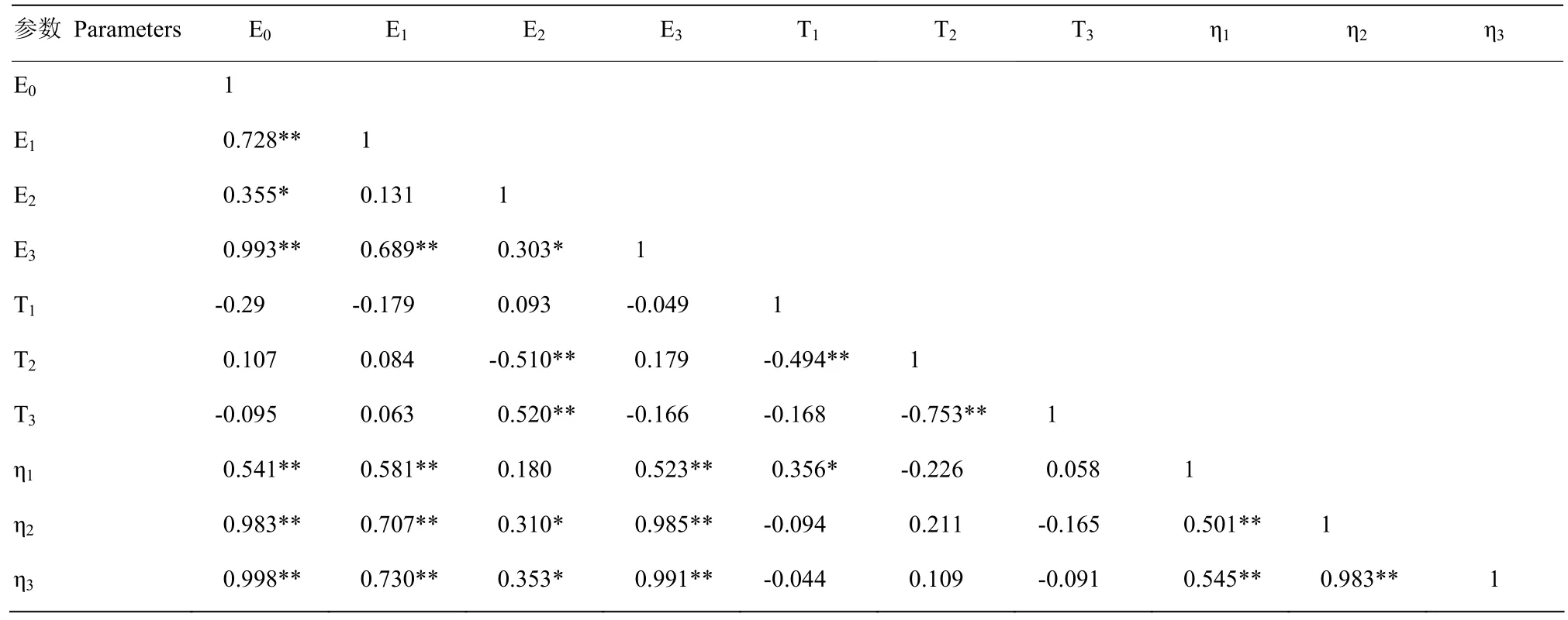
表6 应变模型参数相关性分析Table6 Correlation analysis of the parameters for strain model

2.5 应力松弛参数与品质特征的相关性

表7为应力松弛参数与各项指标的相关性分析，由表7可知，理化指标与弹性参数和黏性系数有显著正相关性（P＜0.05），其中VC和可溶性固形物与E0的相关系数分别为 0.901和 0.757，VC和可溶性固形物与η1的相关性均极显著且相关系数大于0.60；理化指标与松弛时间的相关性不高，仅硬度与T1、弹性与T3之间极显著相关，相关系数分别为0.439和-0.468；质构指标硬度、弹性和黏聚性与弹性参数分别呈显著正相关（P＜0.05），其中，弹性与 E0的相关系数为0.951；ΔE与 E0的相关系数为 0.813；平衡弹性系数E0与VC、可溶性固形物、ΔE和弹性的相关性系数均高于其他各应力松弛参数（P＜0.01）。

2.6 应力松弛模型中参数与各品质特征的回归分析

由表7可知，各指标与应力松弛参数之间有很强的相关性，可通过建立品质特征与应力松弛各参数之间的数学模型来预测猕猴桃品质特征，但表6中应力松弛参数之间有一定的相关性，存在共线性问题，岭回归法是通过对最小二乘法的改进，允许回归系数的有偏估计量存在而补救多重共线性的方法，应用岭回归法建立的预测模型能显著增强估计的稳定性[12-13]。表8为岭回归法的建模结果，由表8可知，模型对 Vc的决定系数达到0.906，效果最好，对可溶性固形物、ΔE、硬度、黏聚性和弹性的决定系数均高于 0.7，模型的显著性P值均小于0.05，具有统计学意义。

2.7 猕猴桃品质特征预测模型的验证

运用2.6建立的品质特征预测模型对验证组进行预测，表9为预测值和实测值差异性检验结果。VC、可滴定酸、可溶性固形物、ΔE和硬度的t检验值均小于2.145（t0.05,9=2.145），表明预测值与实测值之间没有显著性差异。图2为模型对各品质特征的预测值与实测值的相关性图，由图2可知，VC、可溶性固形物、ΔE、硬度、黏聚性和弹性的预测值和实测值之间决定系数分别为 0.882、0.880、0.869、0.691、0.733和0.814，建立的模型能用于猕猴桃品质特征的预测。

表7 应力松弛参数与各项指标的相关性分析Table7 Analysis of correlation of stress parameters and various indexes

表8 应力松弛参数与各品质特征的岭回归分析Table8 Ridge regression analysis of stress parameters and indices

表9 猕猴桃各品质特征预测模型的检验结果Table9 Results of prediction model for quality indexes of kiwifruit

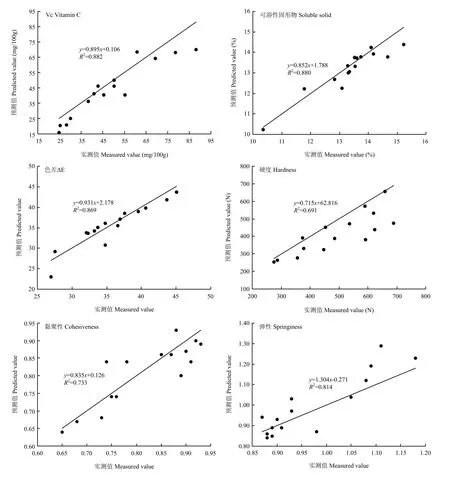
图2 猕猴桃品质特征的预测值和实测值的相关性Fig.2 Relationship between predicted values and measured values about the quality features of kiwifruit

3 讨论

3.1 关于因子分析在猕猴桃品质评价中的应用问题

因子分析是用少数几个因子去描述许多指标或因素之间的联系，即将相关比较密切的几个变量归在同一类中，每一类变量就成为一个因子，以较少的几个因子反映原资料的大部分信息，起到降维的作用。因子分析技术可用于提取猕猴桃的品质特征。张唐伟等[11]通过因子分析筛选出灰分、蛋白质、粗脂肪、pH、L*、b*、失水率和蒸煮损失等8个关键品质指标来评价岗巴羊肉，为岗巴羊肉的发展提供了数据支持；吕健等[10]运用因子分析法筛选出还原糖、复水比、L值、粗蛋白和膨化度这 5个指标来评价桃变温压差膨化脆片的品质。马庆华等[14]运用因子分析法筛选出果实甜脆因子、果重及其他内质因子、果皮质地因子、果实外观因子和其他因子5个主因子来评价冬枣植株的品质，为选择优良的冬枣植株奠定了理论基础。

本试验运用因子分析提出了5个主因子，累计方差贡献率达到77.41%，最终选取出评价猕猴桃品质质量的6个指标，分别为VC、可溶性固形物、ΔE、硬度、黏聚性和弹性。曾凡杰等[15]以色差、质构和 VC为指标评价真空冻干猕猴桃片的品质特征，这与本试验中选取色差、质构和 VC作为特征指标一致。吴旻丹等[16]以硬度、弹性和耐咀性为评价指标建立猕猴桃果实人工模拟咀嚼数学模型，宋小青等[17]运用电子鼻技术建立低温贮藏期猕猴桃的可溶性固形物含量、pH和硬度的数学模型。可以看出，本文通过因子分析提取 VC、可溶性固形物、ΔE、硬度、黏聚性和弹性作为特征品质是合理的。

3.2 猕猴桃应力松驰模型及参数与果实品质特征的相关性

猕猴桃是一种良好的黏弹性物料，在一定的压缩量下，猕猴桃表现出应力松驰现象，其应力松弛特性能反映猕猴桃的品质特征，这与聂毓琴[5]、王海鸥[7]、计宏伟[8]及许永亮[18]等的研究结果一致。本研究通过对‘海沃德’猕猴桃的应力松弛试验，得到力-时间曲线，分别用三元件麦克斯韦模型、五元件麦克斯韦模型和七元件麦克斯韦模型对得到的曲线进行拟合，得到七元件效果最好，这一结果与 HASSAN等[19]的研究结果一致。

由本试验可知，随着猕猴桃的贮藏，E0的变化最明显，松弛时间T2的变化最小，这与BARGALE等[20]得出的小扁豆应力松驰特性的试验结果一致；VC和可溶性固形物与应力松弛模型中的黏性参数和弹性参数都有很强的相关性，这与方媛[21]研究苹果的化学指标与应力松弛模型参数的试验结果保持一致；另外，本研究还得出色差值ΔE与麦克斯韦七元件模型的黏性参数和弹性参数具有很强的相关性，对猕猴桃色泽的研究提供了理论依据；猕猴桃的硬度与应力松弛参数相关性很强，在贮藏的过程中，猕猴桃的硬度会发生变化，这与猕猴桃内部化学变化有关，随着贮藏期的延长，猕猴桃内的淀粉物质转化为糖，果胶水解，猕猴桃的硬度会下降[22]。猕猴桃的品质特征与应力松弛参数之间有很强的相关性，这与许永亮等[18]以米饭为研究对象得出的应力松弛模型参数与米饭化学指标间具有有很高相关性的研究结果一致。此外，平衡弹性系数 E0与猕猴桃各品质指标的相关性系数均高于其他各应力松弛参数（P＜0.01），这一结果与方媛[21]研究富士苹果各品质指标与应力松弛参数的相关性结果一致，可能的原因为平衡弹性系数 E0与物料的硬度相关性最强，是黏弹性物料不能恢复的应变。

本试验建立了‘海沃德’猕猴桃应力模型参数预测品质特征的回归模型，模型对VC、可溶性固形物、ΔE、硬度、黏聚性和弹性预测的决定系数分别为0.882、0.880、0.869、0.691、0.733和0.814。应力松驰参数能预测猕猴桃的品质特征。陆秋君等[23]和KAUR等[24]分别运用应力松弛模型来预测番茄和马铃薯的品质，均取得了较好的结果。

4 结论

‘海沃德’猕猴桃品质特征指标为VC、可溶性固形物、ΔE、硬度、黏聚性、弹性；其应力松弛特性可以用七元件麦克斯韦模型来描述，模型中7个参数分别为 E0（0.524—47.239 N·mm-1）、E1（0.206—15.768 N·mm-1）、E2（0.151—12.966 N·mm-1）、E3（0.252—195.190 N·mm-1）、T1（0.201—23.696 s）、T2（0.188—25.060 s）、T3（0.152—23.918 s）、η1（0.512—34.286 N·s·mm-1）、η2（0.294—273.466 N·s·mm-1）、η3（0.422—39.963 N·s·mm-1）。猕猴桃果实的应力松弛参数与Vc、可溶性固形物、ΔE、硬度、黏聚性和弹性这6个指标具有很好的相关性，运用岭回归对这6个指标所建立的预测模型经验证预测效果良好，该方法具有快速、高效、无损的特点。