市域短期自驾游最优推荐路线问题
常文千 郎鹏 夏永滢 杨悦婷
[提要] 新常态下,人民生活资料极大丰富,自驾游已成为市民短期出行的选择,一种投入少又带来最大满足的游览路线模型亟须提出。本文把满足感作为效用函数,成本投入作为成本函数,基于自驾游满足感与成本函数边际关系,利用条件约束最优化理论求最大化净满足感。影响市民自驾游出行的因素,基本都在模型中有表现。短期自驾游的最优推荐路线模型是在经济学与数学理论下,以旅行的最大满足而不是最小花费和最短距离为目标建立,提出市民短期自驾出行的模型,有一定的实用价值。
关键词:市域;边际效应;自驾游
中图分类号:F062.6 文献标识码:A
收录日期:2019年4月23日
随着国家经济的发展,国民收入增加,人民对文化娱乐生活提出了更高的要求。同时,国家周假政策的落实和我国私家车保有量的上升,客观上允许人们周末外出进行短期的自驾游。2011~2017年旅游人次统计中,我国国内旅游人次增长率在2%~3%,旅游已经成为大众消费中不可少的一项。景点的选择和路线的计划是出行前不可少的一项。规划路线的原则有最短时间、最小金钱和最短行程等,但少有路线能以量化最大满足为准则,海内外学者也鲜有研究。传统的路线规划,如张宇菲等提出的建立以总的旅游时间达到最小的0~1数学规划模型、陈霞等满足路线长度约束的模型等。
我们提出了一种基于最低成本投入而收获最大满足感的短期自驾出行优化路线模型,在市域自驾游的前提下,把满足感的边际效应和成本投入的边际效应引入对满足感-成本模型的量化求最优,使条件最优化模型在最低成本的情况下得到最大产出,为短期市域自驾游路線规划提供新思路。
一、介绍与方法
研究主体有双休日,汽车及家人进行市域旅行。假日出发,周日晚上前返程。空间上“从哪里来、回哪里去”。类别上,从多景点选择;借鉴张宇菲等2016年提出的旅行费用、交通时间、游览时间及旅游体验度指数为目标函数的多目标规划模型,本文把影响最优路线的因素定义为花费、路程、时间和安全等。
根据微观经济学观点,满足感随投入的增大而增大,但满足感存在临界值(最大满足点)。超过,满足感随着投入增加减少,即成本可以转换到更大边际用途(慈善、公益等)。自驾游满足感中,Q为成本量,TU(Total Utility)为总效用,MU(Marginal Utility)为边际效用,其中均衡点表示成本与满足的均衡。水平方向,Q轴大于均衡点,投入大于满足,满足感降低。
投入有价格,投入增多,新增的投入价格升高(d(价格)/d(成本)),经济学解释类似于弹性消费约束函数,这是投入价格弹性,非线性。投入量的增多,投入意愿降低;新投入的满足感降低。满足感函数与旅行者投入是指数负相关关系。等成本线与等产量线的切点为成本投入相同时的最大产出,也为产出相同时的最小成本投入,这是成本论中短期总成本和生产扩展线成立的核心,同理,平衡点实质是新增成本超平面与新增产出超平面的切点。
二、假设与模型
假设游览N个景点,为TA1,…,TAN,其中TAi与TAj(1≤i,j≤N,且i,j∈Z)的距离记为Dij=Dji,出发点到第一个景点距离DS,最后一个景点到出发点距离DE,路程为D,花费为M,时间为T,安全为S,其他因素为E(E为误差)。另,F(N,M,D,T,S,E)为满足感,C(N,M,D,T,S,E)为成本。
模型:MAX{F(N,M,D,T,S,E1)-C(N,M,D,T,S,E2)}
周末自驾游条件下限制N、M、D、T、S与E,最大化满足感与成本模型的理论依据可由图1满足感与成本模型表述,即满足感的边际等于成本的边际。(图1)
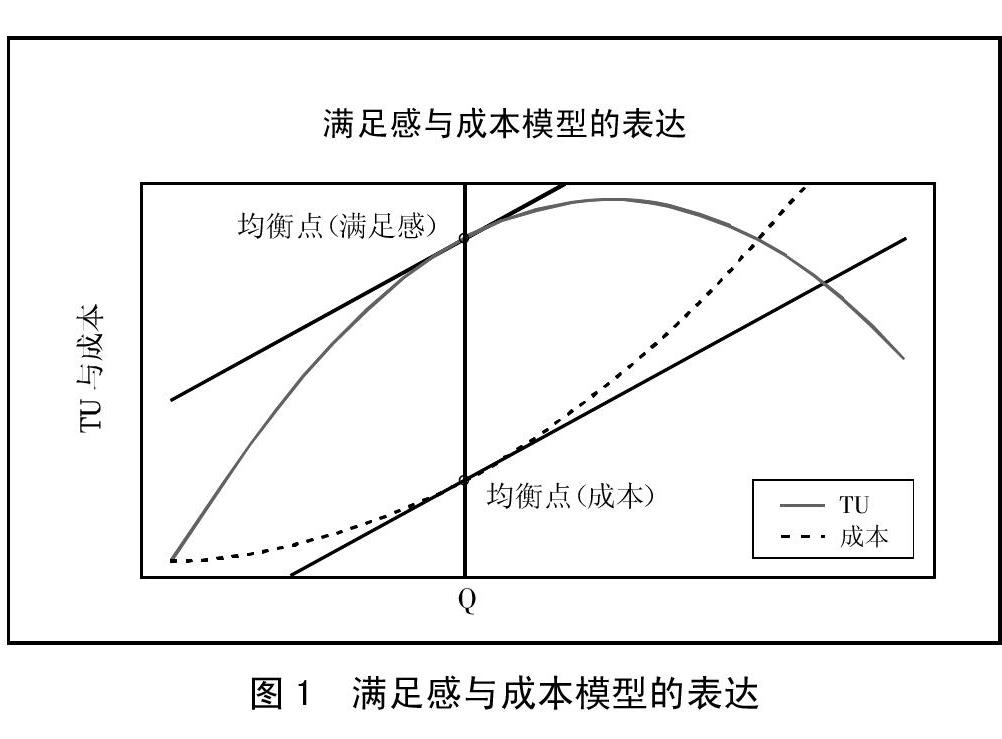
R语言中的非线性优化Rdonlp2包对最优化能给出优良的解决方案,R对于条件约束下的自驾游满足感-成本投入函数的优化结果在1.0021和0.9994间,可断定Rdonlp2包在模拟数据条件下,对于短期自驾游满足感-成本投入函数给出的优化结果会在值x=1附近收敛。

由短期自驾游满足感函数和成本投入函数的数学性质容易求这个函数的可导极大值点在x=1的位置,形式为:
(d{F(N,M,D,T,S,E1)-C(N,M,D,T,S,E2})/dx=0
与模拟的满足感-成本函数取得极大值时x=1的情况一致。所以,Rdonlp2程序包给出的解决方案可靠。
选择唐山市路南区政府为出发点,曹妃甸区多玛乐园、李大钊纪念馆和开发区碧海浴场为游览的3景点,对路线旅行花费(邮费、门票等),距离、时间(车程、等待时间和堵车概率等)和安全(公安部门对路线安全事件统计),指标标准化。
在以上指标对于满足感-成本函数等权重条件下,最优化推荐路线的估计。通过对短期自驾游满足感-成本函数的对比给出最优化路线,为:唐山市路南区政府-乐亭县李大钊纪念馆-海港开发区碧海浴场-曹妃甸区多玛乐园-唐山市路南区政府,如图2所示。(图2)
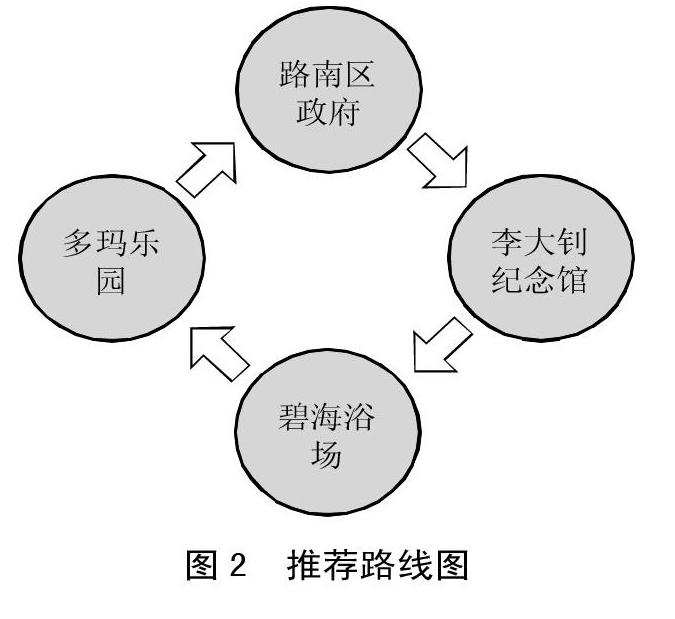
这条路线是平衡等权重条件下给出的最优结果,最大化游客净满意度,对复杂路线的研究也有借鉴意义。
四、总结
(一)效用成本理论与条件约束方法,使得满足感函数和成本投入函数的差在M、D、T和S的限制下达到净满足感最大,即为Net TU|COST={F(N,M,D,T,S,E1)-C(N,M,D,T,S,E2}|N=n,E1,E2最大,成本投入函数的边际等于短期自驾游满足感函数的边际。满足感-成本函数的定义和求解,将这一经济问题量化为条件约束最优化的数学问题,得到理想的路线方案。
(二)通过经验与实际模拟了满足感函数随着成本函数随着成本投入的增加而增加的走势。其中,满足感函数随着成本量的投入先增加后减少符合经济学规律。对于满足感-成本函数的论证可用参数方法(分位数回归等)和非参方法(经验似然函数等)得到逼近。
(三)M、D、T和S独立的假设不一定成立,如路程长短和花费,以及时间消耗有相关关系,安全程度与驾驶时间和路程长短也相关。引入过多指标,会加大负担。对于调查数据的观察分析(VIF,相关系数和偏相关系数),可以去掉一些变量,优化模型,给出更合理的解释。
主要参考文献:
[1]史亚奇.非物质文化遗产传承与旅游经济可持续发展相关性研究[J].中国商论,2017(22).
[2]张宇菲,彭旭,邵光明,等.旅游路线规划问题[J].数学的实践与认识,2016.46(15).
[3]陈霞,陈超,刘凯.多源异构众包数据风景旅行路线规划[J].浙江大学学报(工学版),2016.50(5).
[4]王志伟.微观经济学(上)[M].武汉大学出版社,2013.21.
[5]陈胜科,窦银娣.时间、收入约束条件下生态农业弹性消费选择的函数优化[J].统计与决策,2018(12).

