Q3原状黄土与重塑黄土的土水特性研究

张玉伟，宋战平， 翁效林

(1.西安建筑科技大学 土木工程学院， 陕西 西安710055； 2.长安大学 公路学院， 陕西 西安 710064)

1 研究背景

土水特征曲线SWCC(soil-water characteristic curve)是研究黄土力学特性的基础[1-2]。土体的渗透性、强度、变形等均与土水特征曲线密切相关，土体本构模型建立也常常用到土水特征曲线模型。目前土水特征曲线方面研究已取得了丰硕的成果，理论方面国外学者通过试验提出了多个经典的经验公式[3-8]，得到了广泛的认同与应用，试验方面，王铁行等[9]开展了重塑砂土土水特征试验，研究了砂土密度对吸力变化的影响；王世梅等[10]开展了某滑坡重塑红黏土的土水特征试验，研究了土体应力状态对吸力变化的影响；陶高梁等[11-12]基于分形理论，探讨了黏粒含量和土体压缩变形对土水特征曲线的影响，并利用已有试验数据进行了对比验证；张昭等[13]利用GCTS土水特征曲线仪，测定了无压和固结压力下Q3黄土土水特征曲线，引入“水土体积比”对不同土体进行分析；褚峰等[14]分析了天然干密度和竖向应力对原状黄土土水特性的影响；周葆春等[15]系统分析了土体含水率改变导致其孔隙体积变化，进而研究了孔隙变化下土体的土水特征曲线变化规律；谭晓慧等[16]采用渗析法及滤纸法测定了膨胀土的土-水特性，以Van Genuchten模型为基础对试验结果进行了曲线拟合。可以看出学者们已对土体材料的土水特性开展了较多的研究，并逐渐认识到孔隙变化对土水特性具有重要影响，但目前关于Q3黄土土水特性的研究相对较少，而且Q3黄土具有明显的孔隙结构，孔隙变化对其土水特性的影响非常明显，因此本文系统研究Q3黄土的土水特性，着重考虑Q3黄土的孔隙变化对土水特征曲线的影响，分别制备原状试样和不同孔隙比重塑黄土试样，采用15bar压力膜仪进行Q3原状试样和不同孔隙比重塑试样的试验，系统分析Q3黄土的土水特性，进而采用经典模型对原状黄土和重塑黄土试验数据进行拟合验证，分析现有经典模型对Q3黄土土水特性预测的适用性，并探讨孔隙变化对SWCC的影响规律。

2 Q3原状黄土与重塑黄土的土水特性试验

2.1 SWCC测试方法

采用1500F1型压力膜仪(图1)开展测试[17]，压力膜仪测试装置包括增压泵、保压阀门、密闭压力室和集水管，增压泵提供持续性压力，通过阀门调节试验所需的压力值，压力室提供保压空间，压力室下方陶瓷板浸水饱和时可使室内外压力保持平衡，平衡条件下，土体吸力值与外加压力值相等，土样脱水过程的吸力值变化可通过加压系统实时监测，土体排水量进入集水管，通过排水量可计算出任何试验阶段土体的体积含水率。

图1 1500F1压力膜仪

压力膜仪压力室中的陶瓷板分布有细密的小孔，浸湿时由于受到表面张力作用，小孔表面会形成收缩膜，阻止空气进入内部，压力室内部压力较大，达到土体脱湿的目的，陶瓷板小孔收缩膜内外压差即为基质吸力(见图2)，陶瓷板保压极限值可通过下式计算：

sd=(ua-uw)d=2Ts/Rs

(1)

式中：sd为进气值；Ts为水膜表面张力；Rs为水膜曲率半径。

压力室内土样内部水分受到压差作用逐渐排出，通过实时监测各阶段阀门压力值和集水管排水量，即可得到土体体积含水率和吸力之间的变化关系，最终得到土样的土水特征曲线。

图2 土颗粒与陶瓷板的接触示意图

2.2 试验方案及过程

本文考虑Q3黄土孔隙变化对SWCC的影响，此外还关注现有经典模型对黄土土水特性预测的准确性，分别制备Q3黄土原状试样和重塑试样开展试验，重塑试验考虑了孔隙变化影响。原状试样和重塑试样均由施工现场取土制得，同时进行现场土样的基本参数测试，结果见表1所示。试验过程增压值设置为10、20、40、60、80、100、150、200、250、300、350、400、450、500 kPa。

表1 现场黄土土样基本参数

原状土样采用环刀削样，环刀为直径61.8 mm、高度20 mm的标准小环刀，原状土样如图3所示。拟制备的重塑土样孔隙比分别为0.85、0.8、0.75、0.7、0.65、0.6，不同孔隙比重塑土样由压样器(如图4)来制备，制样原理如下：小环刀体积为V=πr2h=59.99 cm3，根据干密度的定义ρd=ms/V，得到不同干密度ρd所需要一个小环刀样的干土量ms，含水率设定为原状土含水率，可得到小环刀样所需水量，称取干土量ms和所需水量，通过压样筒可依次制备不同孔隙比的重塑黄土试样。

图3 原状土样制备

图4 重塑土样制备

按照《公路土工试验规程》中要求，试样饱和采用毛细管饱和法，土样饱和度大于95%认为符合要求。每级加压平衡后记录集水管读数，每级压力对应的排水量为：

mwj=α·Δh

(2)

式中：α为标定参数，g/mm；Δh为两级压力下集水管读数差，mm。

最大压力稳定时的含水量记作mwf，每级压力下含水率为：

(3)

重力含水率为：

wi=mwi/ms

(4)

可得：

θi=ωiρd/ρw

(5)

式中：mwf为最大压力对应的水重量，g；mwi为加压过程不同压力对应的含水量重量,g；n为加压等级；ωi为加压过程不同压力对应的重量含水率；θ为加压过程不同压力对应的体积含水率；ρd为试样干密度，g/cm3；ρw为4℃水的密度,g/cm3。由上述公式计算得到不同压力等级下土样的体积含水率，结合读取的增压值得到不同试样的土水特征曲线。

3 结果分析与讨论

3.1 原状黄土SWCC

图5为Q3黄土原状试样的试验结果，由图5(a)可看出原状黄土SWCC经历了快速减小、缓慢减小、稳定3个阶段，初始段体积含水率随吸力变化敏感，随着排水的进行，吸力逐渐增大，最终基本达到稳定状态，图5(b) 可看出Q3原状黄土进气值为20 kPa左右，当初始段基质吸力低于100 kPa时，土体内部自由水较多，饱和度较大，自由水排出一部分对吸力大小影响不明显，土体饱和度仍然较高，对于黄土来说，此阶段可认为土体处于饱和阶段(饱和度Sr处于85%～100%)，土体处于饱和湿陷状态，体积含水率的变化对吸力影响很小，土体性质改变也很小；当吸力超过100 kPa而小于400 kPa时，土体进一步排水逐渐进入不饱和状态，土体吸力明显增大，此时土体含水率变化常常引起吸力值的敏感变化，吸力改变也会引起土体性质急剧变化，对于湿陷性黄土而言，此阶段对应着土体强烈湿陷阶段，土体处于不饱和状态(饱和度Sr小于85%，大于残余饱和度)，土体浸水导致含水率变化，引起吸力的明显变化，内部土颗粒粘聚力急剧降低，土颗粒排列更为紧密，宏观上表现为浸水湿陷变形；当吸力超过400 kPa时，土体内部自由水较少，剩余难以排出的结合水，土颗粒之间的吸力作用较大，土体具有明显的结构强度。

3.2 不同孔隙比重塑黄土SWCC

图6给出不同孔隙比重塑试样的土水特征试验结果，图6(a)显示重塑黄土的土水特征曲线与原状黄土整体变化趋势一致，同样可分为3个变化阶段，初始段土体含水改变对吸力影响较小，随着排水的进行，土体吸力变化逐渐增大，最终达到稳定，但可看出孔隙比对SWCC的影响非常显著，孔隙比较大时，相比于孔隙比较小时初始段体积含水率变化对吸力影响更小，说明土体孔隙大时的持水能力更强，随着排水过程，孔隙较大时达到的参与体积含水率较小，孔隙较小时残余体积含水率较大，说明土体孔隙大时的自由水较多，排水量更大；图6(b)显示土体孔隙比对其进气值影响也较为明显，土体孔隙比大时的进气值较小，土体孔隙比小时的进气值较大，说明土体孔隙较大时饱和状态排水更容易，土体孔隙较小时排水困难，这是因为孔隙比较大时，土样内部排水通道更加通畅，自由水迁移阻力相对小，随着吸力增大，自由水逐渐排出，孔隙较小时，土体内部连通性相比大孔隙土体有所减弱，迂曲度增大，自由水在土体内部迁移阻力更大，随着吸力增加土体内部自由水排水相对困难。因此，整体来看孔隙比对Q3黄土土水特性的影响明显，孔隙变化对土水特征曲线的影响不可忽视。

图5 原状黄土土水特征曲线

图6 不同孔隙比重塑黄土土水特征曲线

3.3 理论模型拟合分析

国内外学者根据试验结果及某些假定提出了许多经典的土水特征曲线模型，其中包括Brooks and Corey 模型[3]、Van Genuchten 模型[4]、Gardner 模型[5]、Fredlund & Xing 模型[6]，这些模型多针对于黏土提出，并且上述模型均没有考虑孔隙变化的影响，是否适用于Q3黄土不得而知，因此分别采用Brooks and Corey 模型(简称B-C模型)和Van Genuchten 模型(简称V-G模型)对试验结果进行拟合对比，分析两个模型对Q3黄土的适用性。

Brooks and Corey 模型：

(6)

式中：Se为有效饱和度；Ψa为进气吸力值；Ψ为吸力；λ为土性参数。

又由：

(7)

则B-C模型以体积含水率可表示为：

(8)

Van Genuchten模型：

(9)

以体积含水率来表示：

(10)

式中:a、m、n均为土体参数;m、n的关系一般假定为m=1-1/n或m=1-2/n。

首先对B-C模型和V-G模型参数进行确定，由式(8)可知，B-C模型包括进气值Ψa、孔隙分布指数λ、饱和体积含水率θs和残余体积含水率θr4个参数，其中饱和体积含水率θs可由饱和度换算得到，换算关系为θs=(e/(1+e))Srs；残余体积含水率θr为吸力无穷大时的体积含水率，本文采用Mualem提出确定残余状态体积含水率θr的方法确定[18]。另外进气值Ψa和土体参数λ可以通过试验拟合得到，最终确定B-C模型的4个参数如表2所示。

表2 原状黄土B-C模型参数

V-G模型需要确定θs、θr、a、m、n，其中取m=1-1/n，θs、θr的确定方法与B-C模型一致，参数a、n则由试验数据拟合确定，最终得到V-G模型参数见表3所示：

表3 原状黄土V-G模型参数

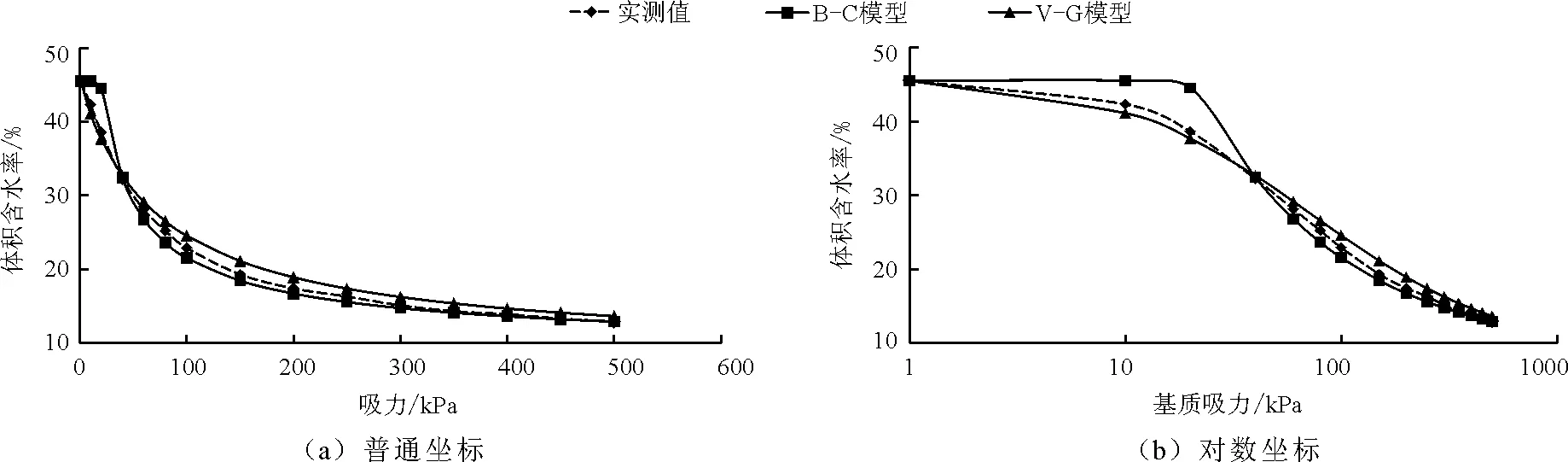
图7 两个模型对原状黄土土水特征曲线的拟合结果

图7给出了B-C模型和V-G模型对原状黄土土水特征曲线的拟合结果，由图7可知V-G模型整体拟合效果较好，尤其在初始吸力段，V-G模型拟合效果明显优于B-C模型，高吸力段两者拟合效果均较好。分析认为B-C模型假定吸力小于进气值时，体积含水率保持为初始值，事实上即使吸力较小时，其微小改变也会引起体积含水率的微小改变，因此在初始吸力段存在偏差，此外模型的参数确定也存在一定误差，导致拟合结果存在偏差；V-G模型给出了体积含水率和吸力关系曲线，尤其初始段精确描述了两者的关系，因此整体拟合效果较好。对于常规土体，孔隙变化不明显，初始吸力段可近似认为体积含水率随吸力的变化不大，可能B-C模型和V-G模型误差不大，但对于具有大孔隙性的非饱和黄土，初始段体积含水率与吸力变化明显，B-C模型预测效果较差，因此对于Q3原状黄土的土水特征曲线可用V-G模型进行预测。

3.4 讨论

由3.3节可看出，V-G模型可描述原状黄土的土水特性，但原模型中没有引入孔隙比，无法描述孔隙比对土水特性的影响。本试验中同时测得不同孔隙比重塑土样的土水特征曲线，试验结果表明孔隙比对重塑黄土土水特征曲线的影响非常明显，引起进气值和初始吸力段明显不同，孔隙变形不得不考虑，但上述两种模型均无法合理考虑孔隙比对土水特征曲线的影响，如果采用上述模型进行预测则需要分别开展不同孔隙比土水特征曲线模型的参数拟合试验，工作量较大，因此采用上述模型进行不同孔隙比的重塑黄土的土水特性预测较为困难，而黄土具有明显的结构性，浸水诱发土体内部孔隙改变非常显著，必然对其土水特性造成更加显著的影响，因此建立考虑孔隙影响的SWCC来预测黄土的土水特性变化具有重要意义，这方面很多学者已经开始了研究，但针对于Q3黄土的研究还比较少见。本文研究表明，对于具有大孔隙的Q3黄土，V-G模型可用于原状黄土土水特征曲线的预测，但对比孔隙比对土水特征曲线的影响模拟无能为力，试验结果表明孔隙变化对土水特征曲线的影响不可忽略，因此后续从孔隙变形入手，建立具有实用性的SWCC模型是一个需要深入研究的方向。

4 结 论

(1)Q3黄土土水特征曲线分为快速减小、缓慢减小和稳定3个阶段，快速减小阶段土体饱和度较高，吸力较小，土体孔隙排水容易，缓慢减小阶段空气进入土体内部孔隙，进气吸力值为20 kPa左右，吸力增大，土体孔隙排水变的困难，稳定阶段土体饱和度很低，土体进入大吸力段，土体孔隙排水不明显。

(2)孔隙比对重塑黄土SWCC有显著影响，孔隙比较大时，初始段体积含水率变化对吸力影响更小，土体持水能力更强，随着排水过程，孔隙较大时达到的残余体积含水率较小，孔隙较小时残余体积含水率较大，孔隙比对进气值影响明显，土体孔隙比大时的进气值较小，孔隙比小时的进气值较大。

(3)分别采用B-C模型和V-G模型与原状黄土试验结果进行了拟合对比，V-G模型拟合效果明显优于B-C模型。但两者均无法预测孔隙变形对土水特征曲线的影响，如何引入孔隙指标描述孔隙变形对土水特征曲线的影响尚需进一步研究。