考虑材料参数空间变异性的堆石坝非侵入式随机有限元研究

王建娥， 杨 杰， 程 琳， 马春辉， 冉 蠡

(1. 西安理工大学 水利水电学院， 陕西 西安 710048； 2.西安理工大学 省部共建西北旱区生态水利国家重点实验室， 陕西 西安 710048)

1 研究背景

随着国内外水利水电资源的不断开发，堆石坝由于可就地取材、地形适应能力强以及稳定性好等优点，成为高坝大库的首选坝型。目前堆石坝正向300m级高度发展。堆石坝的沉降控制是此坝型设计研究的重点和难点，更是确保工程建设、运营安全的重要依据。随着计算机技术的迅猛发展，各种计算分析方法层出不穷，其中有限元法被广泛应用于堆石坝的数值分析中。

然而，一方面，堆石坝中的堆石材料是一种非常复杂的工程材料，其材料参数物理力学特性随机性强且变异性大。另一方面，由于试验测量误差、数值计算理论以及本构模型的局限无法完全模拟实际工程中材料的受力情况等以及由测量误差所带来的统计不确定性等均对计算结果的精度有很大影响。因此，在常规有限元计算中假定大范围的筑坝材料参数为唯一、确定的参数值显然无法反映工程实际，造成计算值与实测值存在较大的误差。因此，若能在有限元计算中考虑堆石料材料参数的空间变异性和随机性，有助于提高堆石坝沉降控制水平，优化堆石坝设计标准、指导大坝施工和运行，从而推动坝工理论的发展。

近年来，众多国内外专家学者致力于在数值计算中考虑材料参数空间变异性的影响，高大钊[1]、包承纲[2]、陈祖煜[3]等均认为应该考虑岩土工程中存在的不确定性因素。考虑材料参数空间变异性的理论分为随机变量理论和随机场理论。其中，随机变量理论是通过离散试验点的变异性来模拟土体参数变异性，该方法假定研究尺度内任意点处的参数相互之间完全无关，无法考虑空间不同点处局部与整体物理力学性质之间的差异性。相比之下，随机场理论能够较好地描述这种空间变异性。Vanmarcke[4]首先提出土体的随机场模型，并提出用波动范围表征土体参数的空间变异性。Griffiths等[5]通过蒙特卡罗模拟(MCS)，实现了边坡可靠度分析的随机有限元方法；Sett等[6]研究了考虑土石料参数空间变异性的动力反应问题；Low等[7]采用随机方法计算土石边坡安全系数和可靠度；在国内，蒋水华等[8]、李典庆等[9]开展了边坡可靠度分析与随机有限元方法结合的研究，并进行了随机多项式展开计算边坡安全系数的显式表达式的研究；祁小辉等[10]采用谱展开法在考虑土体空间变异性的基础上，进行了边坡最危险滑动面的随机分析。目前多数随机场模拟方法存在严格的适用条件，如局部平均法等只适用于矩形或四边形区域；当研究区域不规则、协方差函数形式复杂时，二维第二类Fredholm积分方程求解存在一定困难。相较而言，Cholesky分解方法具有编程简单、适用于不规则边界区域、可提高离散精度等优势，对工程有较强适用性。

上述随机有限元研究主要针对边坡工程进行，而对于堆石坝材料参数的空间变异性研究还鲜有涉及。由于堆石坝材料分区较多且体型较大等原因，致使堆石坝材料参数难免存在空间差异。另一方面，国内外现行堆石坝填筑规范中，通常只对堆石料的干密度以及表征密实程度参数给出了较明确的指标，而对堆石料的级配和母岩性质等的控制则相当粗放。许多研究[11]表明，级配不同时，密实程度相同的同一种堆石料力学特性也有较大差别。因此，虽然筑坝过程中对材料进行了质量控制，但材料的物理力学性质仍具有一定的空间变异性和随机性。

为提高堆石坝沉降控制水平，将随机场理论引入堆石坝沉降值计算中，建立基于Cholesky分解的随机场离散方法。随后，建立堆石坝应力应变分析的非侵入式随机有限元法，以考虑本构模型参数的自相关性以及互相关性。最后，尝试探讨岩土体参数的变异系数对堆石坝坝体沉降值的影响规律。

2 随机场模拟原理

2.1 随机场参数

对随机场的合理离散是随机有限元的重要内容之一，不仅结构需被离散成有限个单元，模型参数也需被离散成一定数量的随机场单元。参数随机场与结构单元可采用不同网格体系，通常每个随机场单元可包含1～2个结构单元[12]，本文随机场单元与结构单元网格划分一致。各参数的随机场单元参数c=(ci,i=1,2,…,ne) (ne为单元总数)的统计特性可由均值μχi和标准差σχi表征，变异系数为：

C·V·(χi)=σχi/μχi

(1)

随机场中任意两点的自相关系数定义为[13]：

ρ[H(xi,yi),H(xj,yj)]=

(2)

式中：H(xi,yi)、H(xj,yj)为中心点空间坐标为(xi,yi)和(xj,yj)的单元参数随机场模拟值； Var[H(xi,yi)]和Var[H(xj,yj)]为中心点空间坐标为(xi,yi)和(xj,yj)的单元方差。

一般采用理论自相关函数来描述堆石料同一本构参数中两个不同空间位置间的自相关性。由于高斯型自相关函数平稳性较好，本文选用高斯型自相关函数：

(3)

式中：τx为空间中两点在水平方向上的相对距离，τx=|xi-xj|；τy为空间中两点在垂直方向上的相对距离，τy=|yi-yj| ；δh为水平波动范围，δv为垂直波动范围，均需根据地质统计或经验确定。从表达式(3)可以看出，自相关函数只与空间中两点的相对位置有关，而与两点的绝对位置无关。

因此，同一参数随机场的自相关系数矩阵为：

(4)

式中：χi为某一参数随机场在计算区域内任意点处的随机特性值，χi=H(xi,yi),i=1,2,…,ne。

2.2 相关对数正态随机场模拟原理

在堆石料随机场的模拟中，常用高斯随机场来模拟，但对于数值大于0且参数间存在一定的相关性的随机参数，直接采用高斯随机场模拟是不合适的。对此，应在高斯随机场的基础上，采用相关对数随机场来模拟堆石料材料参数的随机场。

不同材料参数间的互相关性，可用互相关系数矩阵R表示，m个随机场的互相关系数矩阵表示为：

R=(ρij)m×m

(5)

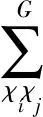
(6)

(7)

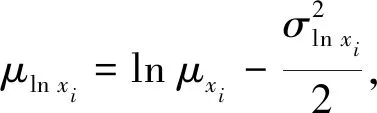
3 堆石坝SFEM实现

面板堆石坝由多个分区组成，各个分区材料均不同，每一种材料的E-B模型均由9个参数确定，若对全部材料分区及材料参数进行随机场模拟，则计算时间较长，且部分参数对计算结果影响很小。为此，首先对E-B模型参数进行敏感性分析，确定对计算结果影响明显的材料参数，有助于简化随机有限元计算，节约计算时间。众多学者分析了E-B模型参数的敏感性，本文根据Zheng Dongjian等[15]采用Morris法的敏感性分析结论，即E-B模型参数K、φ0、Kb对坝体沉降影响较大，对不同材料分区的K、φ0、Kb参数进行随机场的模拟，其余模型参数均采用试验值。由于面板堆石坝各分区材料参数的随机场特征值均不同，因此随机场模拟需按照分区分别进行，最后将模拟结果赋值给各单元，并进行有限元计算。具体步骤为：

(1)根据敏感性分析结果，将敏感性较高的参数作为待模拟的随机场参数，敏感程度较低的参数采用试验数据；

(2)本文选用高斯型自相关函数表征堆石料参数的自相关特征。建立K、φ0、Kb3个参数的自相关系数矩阵，并分别确定垫层区、过渡区、3BI区、3BII区和3C区的均值、变异系数；

(3)鉴于拉丁超立方抽样(LHS)具有适用范围广、抽样估值稳定、样本具有更好的代表性和均匀性等优点，根据文献[16]，1000次拉丁超立方抽样误差很小，可以满足计算要求，因此在满足参数分布规律的基础上，本文采用LHS进行1000次抽样构建独立标准正态随机样本矩阵ξ；

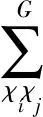
(5)重复步骤(3)与(4)，对垫层区、过渡区、3BI区、3BII区和3C区分别进行参数随机场的离散，得到各个分区的参数随机场离散值，然后将离散值赋值给各对应的单元，进行有限元计算。

其次，针对侵入式随机有限元需修改有限元软件计算程序，且存在工作量大、适用性和灵活性弱等问题，本文在现有商业有限元软件MSC.Marc的基础上，基于Fortran语言实现有限元软件的二次开发，大大提高了计算效率。NSFEM方法可以使随机过程和有限元计算独立进行，更有利于NSFEM方法的推广和使用。其计算流程如图1所示。

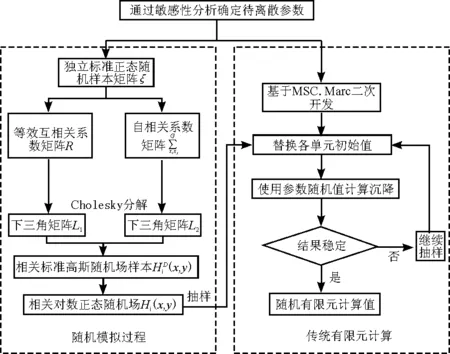
图1 基于MSC.Marc二次开发的非侵入式随机有限元(NSFEM)计算方法流程

4 工程实例

本文用公伯峡堆石坝验证所提方法，对该坝筑坝材料的E-B本构模型参数进行随机场模拟。公伯峡堆石坝FEM模型风格划分如图2所示，模型采用空间8节点等参单元，共1 430个单元、2946个节点。计算中考虑了坝体分期填筑以及分期蓄水对沉降的影响。

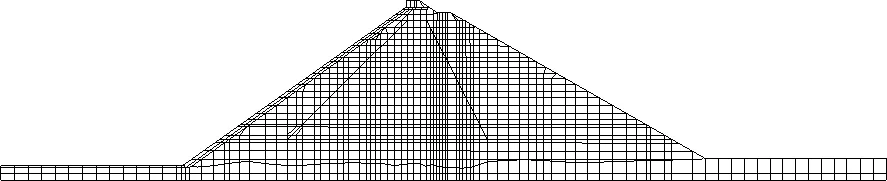
图2 公伯峡二维FEM网格划分

本文将根据布设于坝中部的电磁式沉降仪测线ES2实测数据验证模拟结果的可靠性，测线位于坝左0+130.00 m断面，共计24个测点，如图3所示。

随机有限元计算过程分为：(1)确定材料参数，进行参数随机场模拟；(2)在所得参数随机场基础上，对有限元软件进行E-B本构模型二次开发；采用UltraEdit在DOS环境下调用Marc，进行“非侵入式”有限元计算；(3)随机有限元结果与实测值对比，确定随机场模拟的可靠性从而得到更精确的面板堆石坝应变值。

堆石坝各分区材料的随机场参数取值如表1和表2所示，其中均值、变异系数以及标准差取值参考文献[15]中公伯峡面板堆石坝的均值以及变化范围得出。由于目前随机场理论在堆石坝中的应用鲜有涉及，大多应用于边坡可靠度分析中，Ronold[17]、程强等[18]、吴振君等[19]得出了不同地区边坡工程的土体参数波动范围的统计值，但由于堆石坝各分区的堆石料均由人为粒径控制以及碾压等，不适用于土体参数波动范围的统计规律。对于同一分区的筑坝材料，在经过人为筛选、控制后，材料差异较小，因此可将堆石坝各分区的水平和垂直波动范围取为所在分区的几何尺寸。

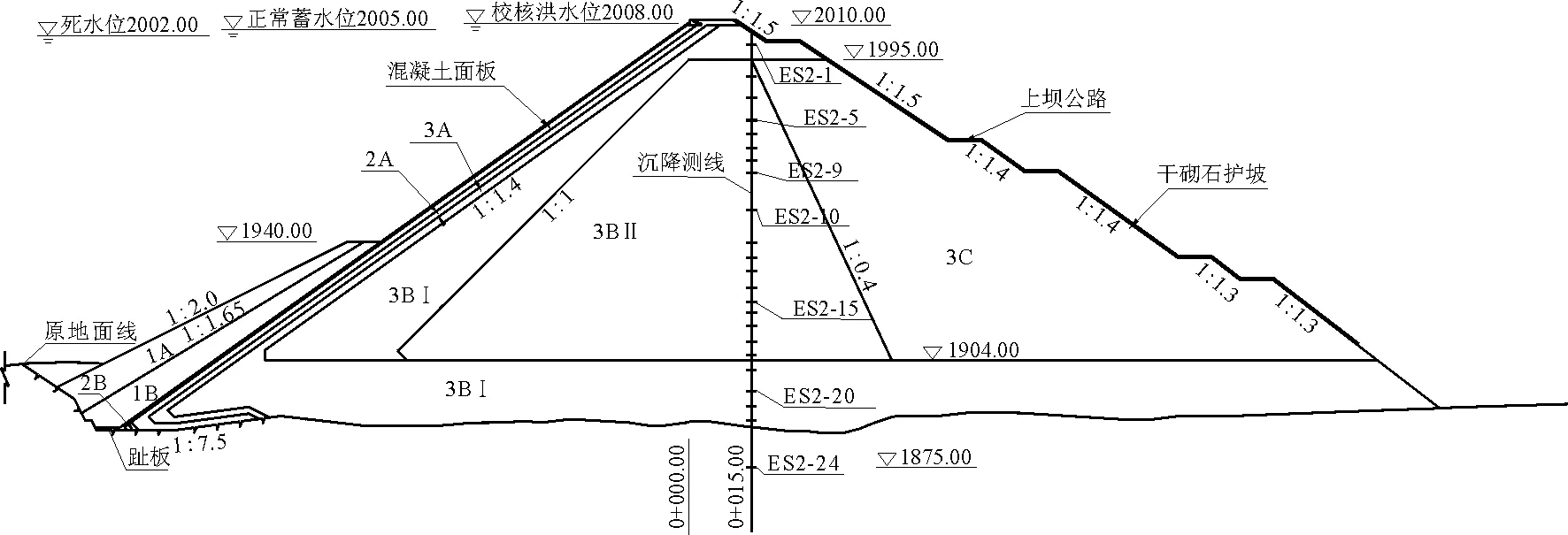
图3 公伯峡堆石坝左0+130.00 m剖面材料分区及测点分布图(单位：m)

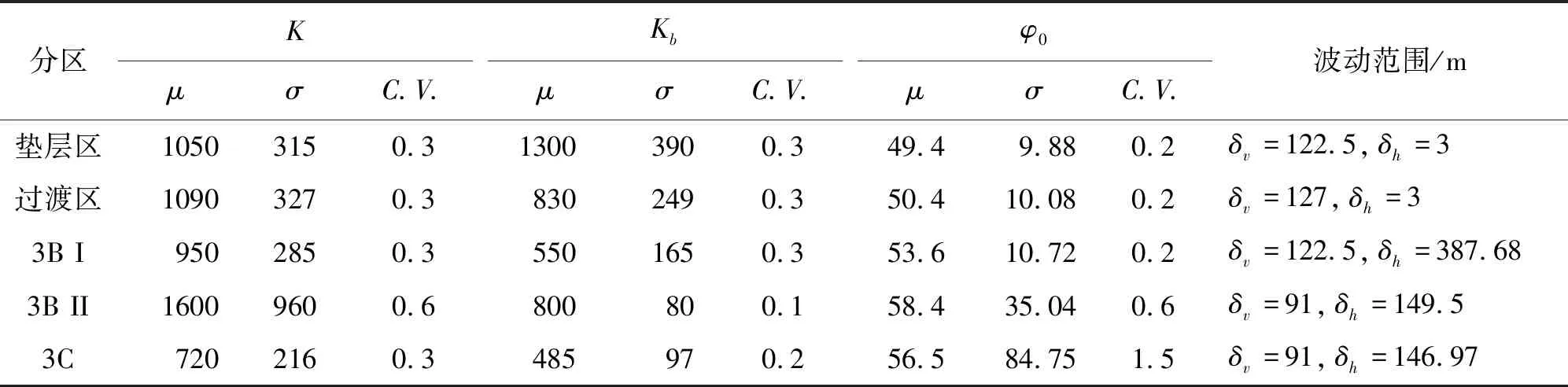
分区KμσC.V.KbμσC.V.φ0μσC.V.波动范围/m垫层区10503150.313003900.349.49.880.2δv=122.5, δh=3过渡区10903270.38302490.350.410.080.2δv=127, δh=33B I9502850.35501650.353.610.720.2δv=122.5, δh=387.683B II16009600.6800800.158.435.040.6δv=91, δh=149.53C7202160.3485970.256.584.751.5δv=91, δh=146.97

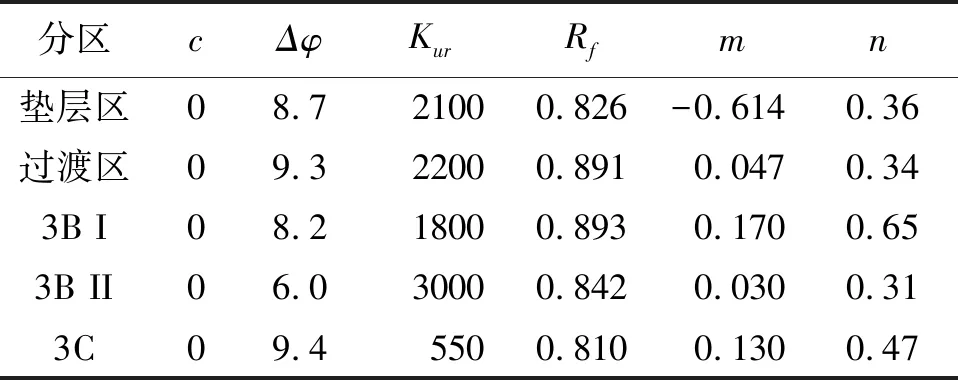
表2 堆石料其他材料参数取值表

在确定随机场参数的基础上，提取面板堆石坝二维模型的节点坐标数据，按照本文第3节提出的步骤分别进行各个材料分区参数K、φ0、Kb随机场的模拟。将各分区的模拟值赋值给相应的单元，得到整个坝体断面的参数随机场，其中随机场模拟的一次实现结果如图4所示。

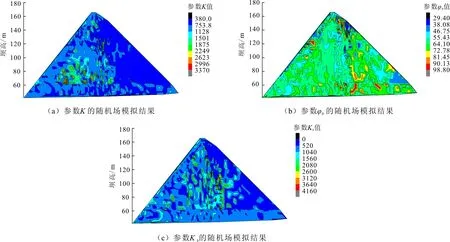
图4 参数随机场模拟的一次实现结果

由图4中可以看出，每个单元的材料参数取值均不同；由于本文分别对各个分区分别进行随机场离散，因此同一个分区内同一参数在不同单元的取值服从高斯函数；由图4也可看出，材料参数随机场极端值较少，这是因为高斯型自相关函数稳定性较好。

采用基于MSC.Marc二次开发的随机有限元方法进行随机场的离散，分别利用1 000次随机场离散结果进行有限元计算，1 000次计算结果均明显大于常规FEM方法计算值，对1 000次模拟结果取均值，其沉降值如图5所示。图5为坝体断面最大累计沉降等值线图，采用随机有限法计算得坝体蓄水完成时断面最大沉降为70.12 cm，位于坝体中部偏向下游，这是由于3C区堆石质量标准略低于3BⅡ区。因此，坝体整体变形规律符合常规规律，本文提出的随机有限元方法基本正确。图6为常规有限元计算得到的断面最大累计沉降等值线图。通过比较图5与6可知：(1)图5中的等值线较图6波动略明显，这是由于非侵入式随机有限元考虑了材料参数空间变异性，材料参数具有一定随机性，使得不均匀沉降值增加所造成的；(2)图5出现了零星的封闭等值线，表明考虑材料参数空间变异性之后，由于随机性引起的不均匀沉降增加；(3)随机有限元计算得到的坝体最大沉降值为70.12 cm，常规有限元计算值为60.05 cm，实测最大沉降值为68.52 cm，因此随机有限元的计算结果大于常规有限元，更接近于实测值。

图51000次随机有限元计算的平均最大 图6常规有限元计算的最大断面

断面累计沉降等值线图(单位：m) 累计沉降等值线图(单位：m)

将常规有限元计算值、测线ES2的实测沉降值与非侵入式随机有限元计算值进行对比，如图7所示。由图7可知：(1)NSFEM计算结果明显大于FEM，这是由于面板堆石坝在材料选用、施工填筑以及材料参数测定中有很大的随机性，NSFEM按对数正态分布规律对材料参数进行离散，考虑了材料参数可能存在偏离均值的情况，因此所计算的沉降值大于常规有限元的结果；(2)目前的FEM方法计算值与实测沉降值有着明显差距，尤其在坝体中部以及上部，实测沉降值明显大于计算值，这符合现有堆石坝实测沉降值大于有限元计算值的实际情况；(3)NSFEM计算值与实测值比较接近，证明NSFEM方法通过考虑筑坝材料的随机性和不均匀性，其计算值更符合实际工况；(4)在坝体中部以及中上部，NSFEM计算值与实测沉降值拟合较好，在坝体下部略有误差，但整体拟合良好。

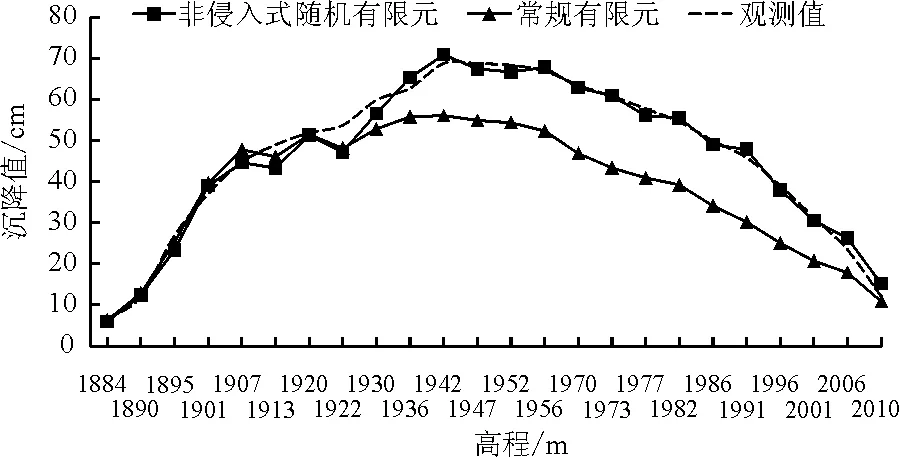
图7 坝体断面最大累计沉降实测值与计算值对比

NSFEM与实测值的相对误差平均约为5%，FEM与实测值的相对误差平均约为20%，随机有限元模拟值尤其是坝体中上部模拟值明显更加接近于实测值。

5 筑坝材料变异系数对坝体沉降的影响规律

在上述研究的基础上，分析筑坝材料变异系数对坝体最大沉降值的影响，由于最大沉降值往往出现在3BII区和3C区，本文在控制其他分区其他材料参数以及参数统计特征值不变的前提下，分别对3BII区和3C区参数K、φ0、Kb的变异系数对坝体沉降的影响进行了研究。

图8反映了3BII区和3C区参数K的变异系数，即C.V.(K)对坝体沉降的影响规律。由图8可看出：(1)不同变异系数在坝体下部的沉降值基本重合，表明材料参数的变异性对坝体下部的沉降值影响较小。这是由于坝体下部受到岩土地基的约束，因此沉降值变化不大；(2)随着C.V.(K)的减小，坝体最大沉降值逐渐减小。这是由于C.V.(K)减小，材料相对均匀，不均匀沉降减少；(3)随着C.V.(K)的减小，折线之间的间距越来越小，表明坝体沉降减小的速率逐渐减缓，达到最小沉降值之后不再变化。计算表明，以高程1 952 m处的沉降值为例，C.V.(K)每减小0.1，3BII区沉降值的减小速率由5.09%减小到1.7%，3C区沉降值的减小速率由0.33%减小到0.13%；(4)图8(a)较图8(b)折线之间的间距更大。随着C.V.(K)的减小，3BII区最大变化率为5.09%，3C区最大变化率为0.33%，3BII区明显大于比3C区，表明坝体沉降对3BII区的敏感度大于3C区；(5)图8(a)较图8(b)最大沉降值的最小值更小，如C.V.(K)=0.05时，3BII区最大沉降值为55.91 cm，而3C区最大沉降值为68.18 cm，表明实际工程中通过提高3BII区材料参数的控制标准可以更有效控制坝体沉降值。

3BII区和3C区C.V.(φ0)对坝体沉降的影响规律与图8相似，不同之处在于：在C.V.(φ0)与沉降的关系图中，曲线间距更大，表明坝体沉降值对C.V.(φ0)的敏感性更大。C.V.(Kb)对坝体沉降影响规律的不同在于：(1)随C.V.(Kb)变化，坝体沉降变化不明显，尤其是3C区出现多条折线重合的现象，表明坝体沉降对C.V.(Kb)敏感性很小；(2)C.V.(Kb)很大时对应的坝体最大沉降值仍较小，进一步证明坝体沉降对C.V.(Kb)敏感性很小。

图9为3BII区和3C区材料参数变异系数对最大沉降值影响规律图。

由图9(a)可知：(1)随着材料参数的变异系数减小，坝体沉降值随之减小且曲线斜率也随之减小，减小到一定值时，坝体最大沉降值基本保持不变，进一步验证了图8的结论；(2)当C.V.(φ0)>0.1时，随着C.V.(φ0)的增大，最大沉降值明显增大，当C.V.(φ0)>0.3时，随着C.V.(φ0)的增大，最大沉降值急剧增大；(3)当C.V.(K)>0.1时，随着K的增大，最大沉降值明显增大，当C.V.(K)>0.7时，随着C.V.(K)的增大，最大沉降值快速增大；(4)参数Kb的变异系数的变化对最大沉降值基本没有影响。

由图9(a)与9(b)对比可知：图9(b)相对图9(a)3条曲线的斜率均较缓，图9(a)中K、φ0、Kb的变异系数曲线最小值分别为66.27、73.19、72.05 cm，图9(b)中曲线的最小值分别为70.37、74.48、70.42 cm。图9(a)中的值较小，说明沉降值对3BII区材料参数特征值更为敏感，控制3BII区材料参数变异性更有利于控制坝体最大沉降值。

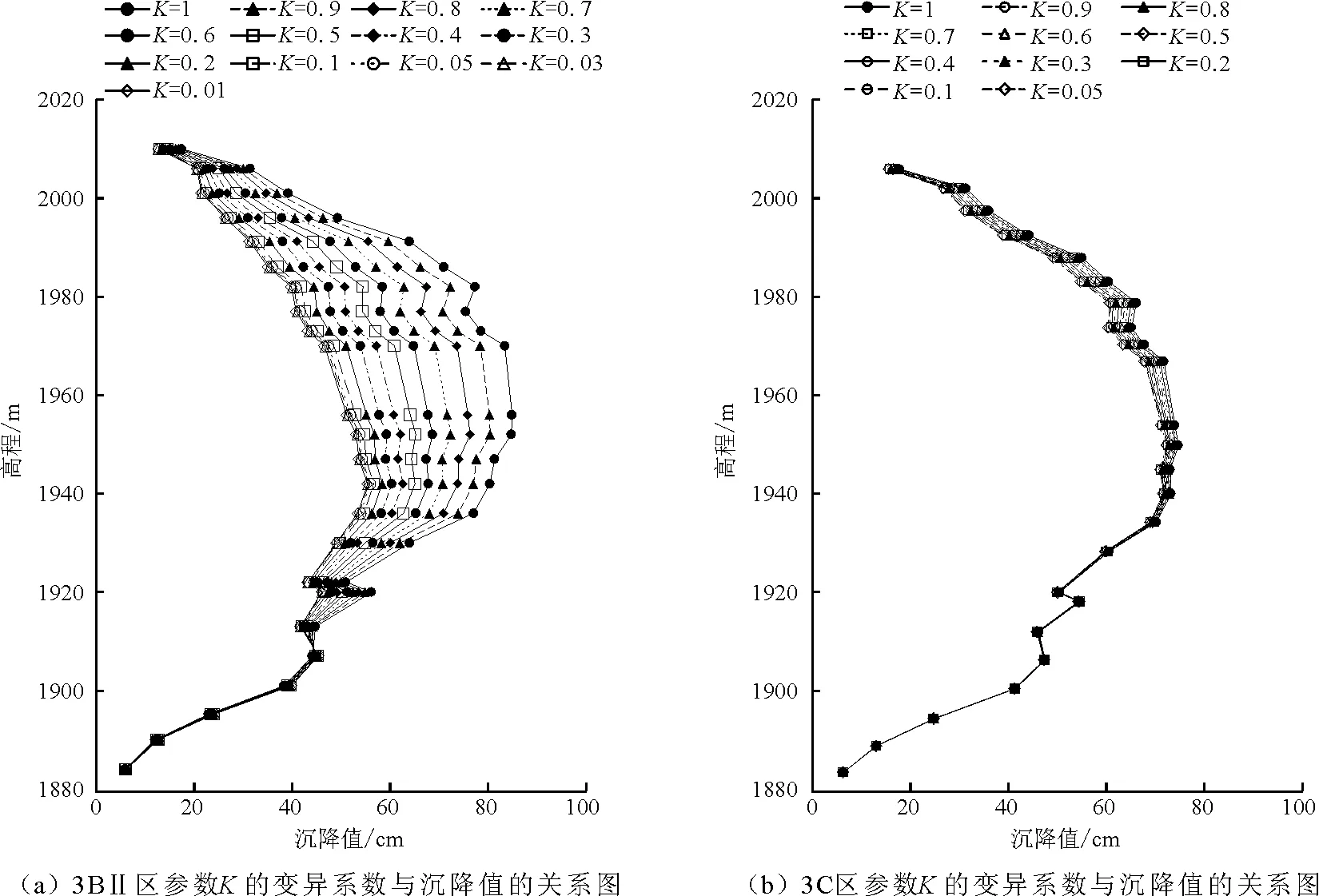
图8 参数K的变异系数对不同高度坝体沉降的影响规律

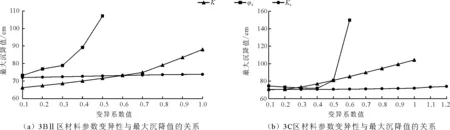
图9 材料参数变异性与最大沉降值的关系

6 结 论

为了考虑筑坝材料的不确定性因素对坝体沉降计算结果的影响，本文引入随机场理论因素，取得了良好的效果。本文提出的方法适用于形状不规则的坝体填筑料分区区域，对堆石坝设计和施工中填筑材料的控制指标的制定具有重要的参考意义。将研究内容与结论总结如下：

(1)在基于Cholesky分解的随机场模拟方法的基础上，结合堆石坝的材料参数特性，进行了基于有限元软件MSC.Marc的二次开发，提出了堆石坝的非侵入式随机有限元方法；

(2)通过工程实例验证，表明材料参数空间变异性对堆石坝变形计算结果影响明显，最大沉降值明显大于常规有限元计算值，更接近实测值，更符合工程实际情况；

(3)探讨了表征岩土体参数的变异系数对堆石坝沉降值的影响规律：坝体沉降值对3BII区材料参数的变异性敏感程度较3C区更大；材料参数按照敏感性从大到小排序为φ0、K、Kb。

(4)得出了最大沉降值与变异系数的曲线图，可确定最大允许沉降对应的变异系数，进而确定各个材料分区材料参数概率分布的均值和标准差，对工程实际具有一定的参考意义。