基于Copula函数的锦河与连锦河洪水遭遇分析

蒋 楠， 高 成， 夏 欢

(1.河海大学 水文水资源学院， 江苏 南京 210098； 2.河海大学 农业工程学院， 江苏 南京 210098)

1 研究背景

洪水发生及产生的灾害是难以避免的自然现象。作为能够有效抵御洪水的手段之一，防洪工程措施在防治大洪水中起到了不可小觑的作用。在拟定防洪方案过程中，洪水计算是不可或缺的。因此在进行防洪评价的洪水计算部分有必要进行洪水遭遇的概率分析。利用Copula函数进行多变量水文概率分析已十分常见。例如：王占海等[1]使用多维Copula函数研究长江干流宜昌水文站各设计标准洪水空间分布的合理性。侯芸芸等[2]在基于三变量Copula函数算法上建立了峰量以及历时的联合概率分布模型。陈璐等[3]利用多维Archimedean Copula函数计算长江干支流沿岸水文站洪水发生时间及量级遭遇的概率，李子远[4]采用Gumbel Copula函数模拟两河洪峰发生时间的双变量联合分布，以此计算洪峰遭遇概率。叶姗姗等[5]运用Copula函数风险概率模型对宿迁市暴雨雨型风险率进行了研究；高玉琴等[6]采用三维G-H Copula函数对秦淮河流域的洪峰和洪水位进行了风险率的计算；王亚雄等[7]用最优Copula函数进行了飞来峡水库坝址洪峰和最大7日洪量的联合重现期与边缘分布重现期的比较；Salvadori等[8]运用二维的Copula函数对降雨历时和降雨强度的联合概率分布进行模拟。Poulin等[9]分析了概率模型的多种边缘分布函数特性，并将之应用于实例。Hochrainer-stigler等[10]对Copula函数的原理结构进行了研究并用于系统整合风险分析。但以上的Copula函数研究还存在一定局限性，主要为以下几点：

(1)在水文频率计算中，经验频率法是基于实测资料进行经验公式计算的一种方法，它需要足够长的实测系列资料才能满足计算精度，其次，该方法在外延预测方面效果不佳。

(2)大多数水文变量服从偏态分布，如果假设这些变量属于正态分布会使得计算结果的精度不高。

(3)部分地区有高潮出现时，其降雨类型复杂，Copula函数在雨潮组合遭遇的风险分析方面还有待进一步研究。

(4)Copula函数在干支流特大洪水同时发生的分布模型还需要探索。

在以上研究基础上，本文主要研究应用Copula函数计算锦河和连锦河洪水遭遇概率，收集江西省高安和宜丰两个水文站的实测洪峰流量资料，采用年最大值法选取年最大流量，并计算其经验频率，其边缘分布为P-Ⅲ型曲线。然后选择4种常用的Archimedean Copula函数对锦河和连锦河洪水遭遇的联合分布概率进行研究，经相关参数估算后，以AIC[11]和OLS值最小的原则来选出模拟效果最佳的Archimedean Copula函数，将其应用于计算锦河和连锦河洪水的同现概率及条件概率，对计算进行分析研究，并可将洪水遭遇概率及河道水面线的计算成果应用于实际工程项目中。

2 研究区概况

锦河流域位于江西省高安市西部。本文研究内容为流域内的锦河与连锦河的洪水遭遇情况。锦河起源于湘赣交界的幕阜山脉海拔高程为628.6 m的东麓坪子岭。全长304.55 km，流域面积7 884 km2，是赣江下游西岸的一条重要支流，也是流经高安的第一大河流。锦河干流城区段河长约13 km，宽约150～300 m，河床底高程20～24.5 m，较河岸低8.0～12.0 m，河道纵坡约为(0.6～2.0)/10000。其流域水系图见图1。

图1 锦河流域水系图

连锦河，又名港溪水，位于锦河干流左岸，为高安城区主要支流之一，其河道左岸地势较高，右岸城区段的地势低洼。该河流发源于高安市奉新县交界的米岭南麓，自北向南流经仓下村、汪家圩、港溪、水口庵，至连锦桥进入城区，于五口桥汇入锦河。流域面积89.85 km2，主河道全长23.01km，主河道纵比降1.91‰，高安城市规划内连锦河的河段长约5.5 km，一般河宽50～80 m。

3 研究方法

3.1 边缘分布函数计算

Copula函数计算概率之前首先要确定水文变量的边缘分布函数。P-Ⅲ型曲线能够较好地拟合暴雨洪水等变量的概率分布，是国内一种应用较为广泛的边缘分布函数。本文给定高安站及宜丰站的洪峰流量服从P-Ⅲ分布函数[12]，其概率密度函数如公式(1)所示。

(1)

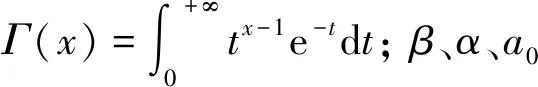
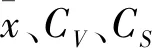
锦河流域内有重要的水文测站高安站，其实测洪水能较好地代表锦河洪水过程。该水文站位于高安市城区高安大桥上游200 m处，控制集水面积为6 215 km2，有1964、1991-2016年历年实测洪峰流量资料，经附近贾村站插补延展有1964年至2016年洪峰流量资料。宜丰水文站位于锦河左岸支流连锦河，控制流域面积为519 km2，河道坡降为1.91‰，现有1957-2016年实测洪峰流量资料。资料条件系列长，数据精度高，可作为连锦河水文站，由于连锦河上游有一碧山水库，其上游集水面积为31.7 km2，坝址以上河长8.70 km，平均坡降为5.58‰，水库正常蓄水位58.01 m，总库容1 979×104m3，考虑其调蓄作用，进行了调洪计算，在边缘分布计算中洪峰流量将减去其调蓄流量。对宜丰站、高安站流量进行排频分析，并将高安站1913年调查最大流量作特大值处理，采用P-Ⅲ曲线适线，可进行洪水频率计算并得到锦河和连锦河P-Ⅲ分布函数的统计参数见表1。

表1 锦河和连锦河P-Ⅲ分布函数统计参数值表

3.2 边缘分布函数的检验

水文变量的理论分布是否能够准确代表变量总体的分布，需要进行假设检验。为保证检验的准确性，本文采用Kolmogorov-Smirnov检验、Anderson-darling检验以及均方根误差(RMSE)来分别衡量高安站和宜丰站洪峰流量的边缘分布函数。

将两个水文站的洪峰流量系列导入SPSS中进行K-S非参数检验，得出两个测站的P值均为0.2，大于0.05，表明该边缘分布通过K-S检验。Anderson-darling检验中计算出的高安站与宜丰站的P值分别为0.26和0.29，大于0.05，该分布通过了Anderson-darling检验。计算得出两个测站的RMSE分别为0.025和0.022，表明二者的均方根误差均较小。根据上述检验，可以确定两站的P-Ⅲ分布可作为边缘分布函数。

3.3 Archimedean Copula函数

Archimedean Copula函数可用于构建水文界常见的联合概率分布模型，它的结构形式多种多样，不同结构对不同类型的洪水拟合效果有较大差异，本文选用以下4种对称式的结构形式。

(1)Gumbel-Hougaard Copula[7]：

C(u1,u2)=exp{-[(-lnu1)θ+

(-lnu2)θ](1/θ)}θ∈[1,+∞)

(2)

(2)Clayton Copula[7]：

C(u1,u2)=(u1-θ+u2-θ-1)-1/θ

(3)

θ∈(0,+∞)

(3)Ali-Mikhail-Haq Copula[7]：

C(u1,u2)=u1u2/[1-θ(1-u1)(1-u2)]

(4)

θ∈[1,+∞)

(4)Frank Copula[7]：

(5)

θ∈R

式中：C为Copula函数；u1和u2为边缘分布函数，u1=F1(x1)，u2=F2(x2)；θ为相关参数。

3.4 Archimedean Copula函数参数估计

估计4种函数的参数是一个不可或缺的环节。以相关指数法来计算上述4种洪峰联合分布函数的参数。相关指数法是依据Kendall秩相关系数τ[13]来计算Copula函数的参数θ，两参数的函数关系式见表2。

表2 Copula函数的τ与θ函数关系[14]表

根据SPSS软件分析得出两站洪峰流量Kendall秩相关系数τ为0.174，根据函数关系计算出的参数θ值见表3。

表3 Copula函数的θ计算成果表

3.5 Archimedean Copula函数选择

由上节计算出函数的θ，可建立两水文站洪峰流量的4种Archimedean Copula函数的联合概率分布，以上函数是否能够较为准确地拟合两变量之间的关系，需要进行函数拟合检验，然后通过优度评价准则选择出一种拟合效果最好的Copula函数。

3.5.1 图形评价分析法 本文主要利用Q-Q图的方法直观表示拟合效果的优劣。将经验和理论联合概率值点据呈现在一张图上，若各点大致位于y=x线左右，则说明构建的模型有一定可靠度。二维经验联合概率计算见公式(6)：

Femp(xi1,xi2)=P(X1≤xi1,X2≤xi2)

(6)

式中：Femp为经验联合概率；ng,k为满足X1≤xi1,X2≤xi2的联合观测数量；n为系列长度。

将4种Copula函数的理论与经验联合概率值点绘为散点图，见图2。

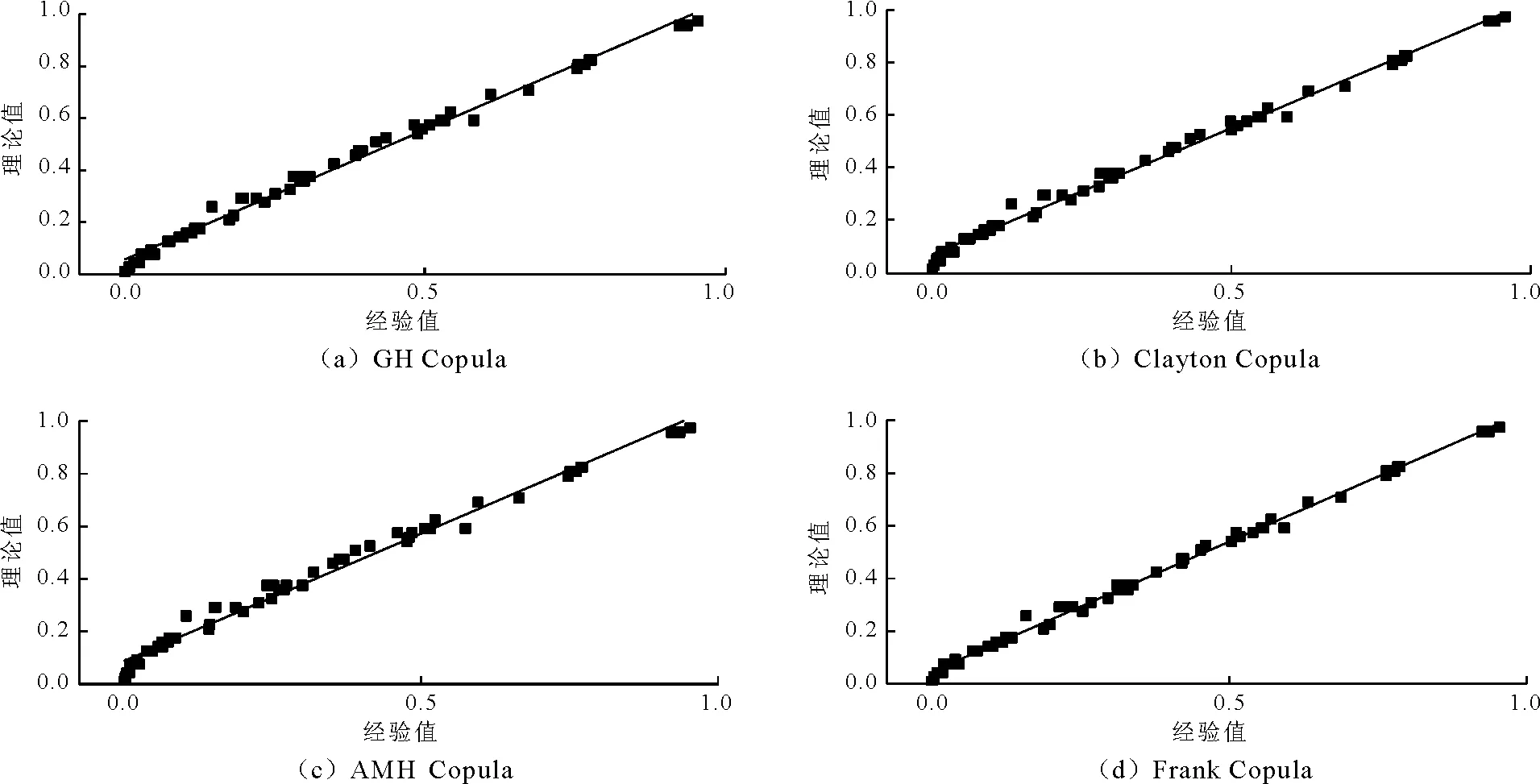
图2 4种Copula函数的理论与经验值Q-Q图

根据Q-Q图可见以上4种Copula函数的理论与经验联合概率点据均位于45°线上下，则可说明这4种Copula函数构建的联合概率分布模型的模拟效果较为满意。

3.5.2 最优Copula函数选取 为选出对锦河和连锦河洪峰遭遇拟合效果最好的Copula函数，需采用优度评价准则即AIC准则及OLS准则来评价4种Copula函数。

AIC准则结构如下所示：

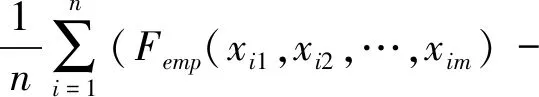
C(ui1,ui2,…,uim))2

(7)

AIC=nln(MSE)+2k

(8)

式中:m为函数的维数;k为模型参数的数量。AIC值越小，表明函数的联合概率分布拟合效果越佳。

OLS准则结构如下：

OLS=

(9)

根据公式(8)与(9)计算出4种Copula函数的AIC值与OLS值如表4所示。

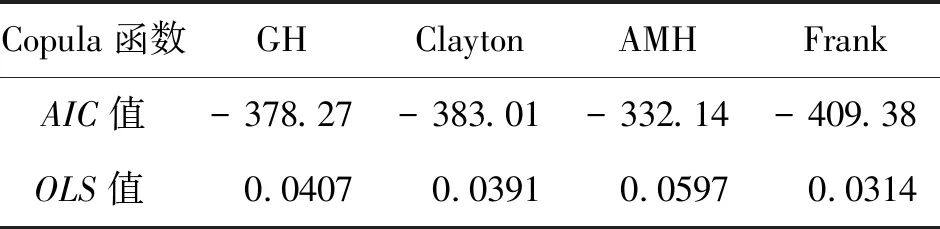
表4 AIC值与OLS值计算成果表

由表4可知AIC值与OLS值最小的均为Frank Copula函数，则可说明Frank Copula函数是模拟该流域洪水洪峰遭遇概率效果最佳的函数，因此，本文选择Frank Copula函数进行锦河与连锦河洪水遭遇概率分析。

4 干支流洪水遭遇分析

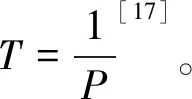
洪峰流量(x1,x2)的联合分布为F(x1,x2)，则：

F(x1,x2)=P(X1≤x1,X2≤x2)

=C(u1,u2)

(10)

锦河和连锦河同时发生某一设计标准的洪水的概率为重现概率，以H0表示，则:

H0(x1,x2)=P(X1>x1,X2>x2)=1-u1-u2+C(u1,u2)

(11)

在锦河发生一种重现期的洪水前提下，连锦河发生某一数量级的洪水概率如公式(12)：

(12)

锦河和连锦河的洪峰联合概率分布、同现概率与条件概率如图3、4、5所示。

图中Qxi为锦河的洪峰流量(m3/s)，Qyi为连锦河的洪峰流量(m3/s)。由图4可知，锦河的洪峰流量大于5 000 m3/s(约100年一遇)和连锦河的洪峰流量大于1 200 m3/s(约100年一遇)的洪水发生的概率极小。锦河和连锦河的洪水同现概率随着洪水的量级的增大而减小，联合概率随着洪水的量级的增大而增大。在锦河发生20年一遇的洪水工况下，连锦河发生同等量级的洪水概率明显增加。在锦河发生一特定数量级的洪水前提下，连锦河发生洪水的概率随着洪水量级的增加略有增加。以上规律经验证符合两河洪水发生的概况。表5统计了100年一遇量级以下锦河和连锦河的洪水遭遇的概率。

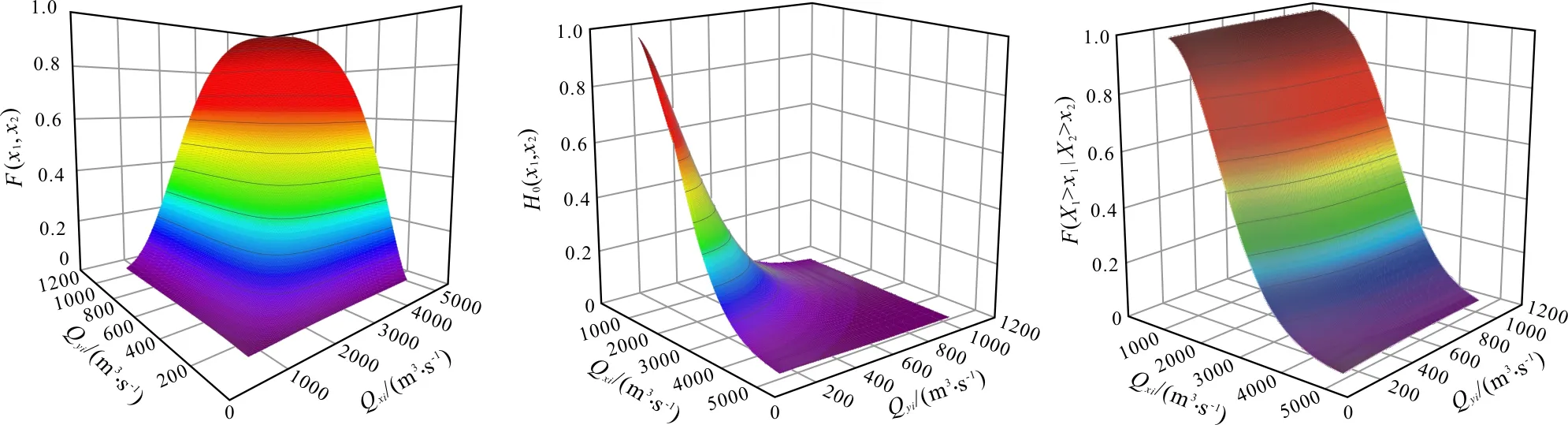
图3锦河与连锦河联合概率分布图 图4锦河与连锦河同现概率分布图 图5锦河与连锦河条件概率分布图

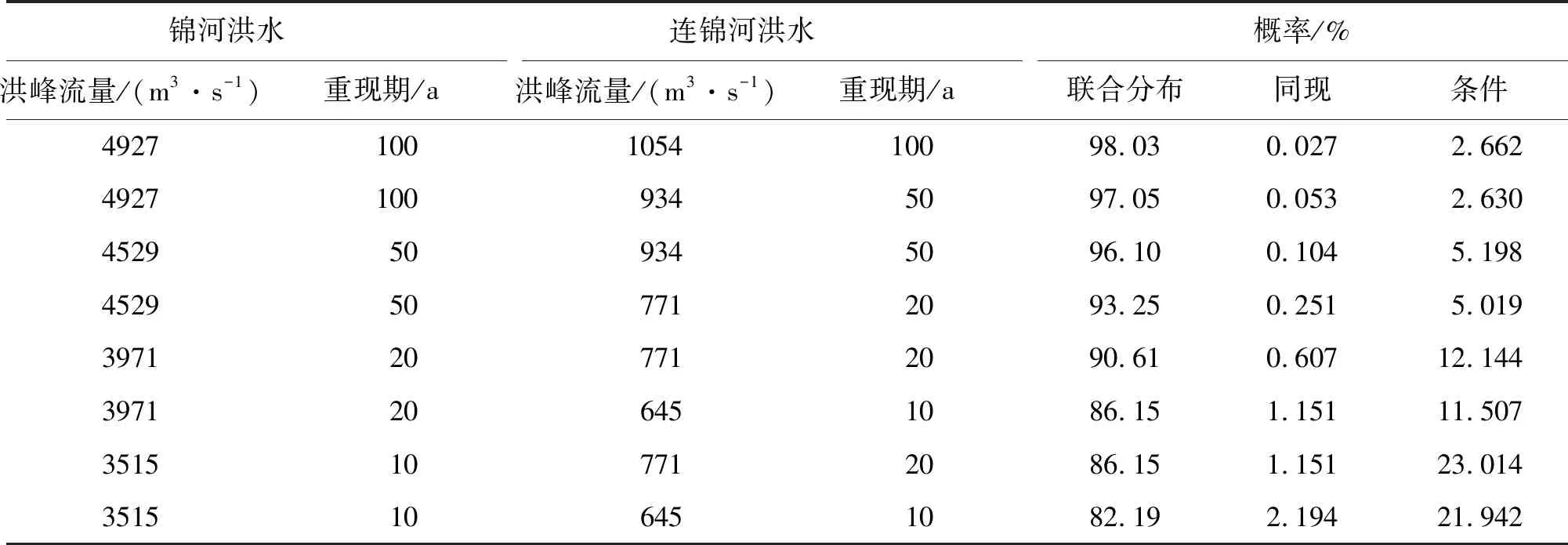
表5 锦河和连锦河洪水遭遇概率计算表

由表5可知，锦河和连锦河同量级洪水同时出现的概率较小，在锦河出现100年一遇工况的洪水时，连锦河发生同一设计标准洪水的几率仅有2.662%。两河发生20年一遇量级洪水的概率较大，在锦河发生10年一遇以上洪水的情况下，连锦河同时发生20年一遇以上洪水的概率高达23.01%。由此可见锦河和连锦河大量级洪水遭遇的可能性较小，而小量级洪水遭遇的机率较大，该结论与《赣江流域水文年鉴》中近几十年的洪水统计资料相符合。

5 水面线计算

根据水文年鉴上的洪水实测资料，估算连锦河洪水传播时间约为2.8 h。锦河上高水文站到高安站距离为79 km，洪水传播时间约为18 h。因此，锦河干流与连锦河支流洪峰在时间上是错开的，同时遭遇的几率甚小，所以不按同频遭遇考虑。工程研究的河段对于锦河而言是从徐王村到筠州大桥，桩号为-K5+910～K1+523，连锦河的研究河段为平安大道到连锦河河口，桩号为-K2+966～K2+027。

5.1 模型原理

MIKE11一维河网汇流模型采用非恒定流圣维南(Saint-Venant)方程组构建[19]。

连续方程：

(13)

动量方程：

(14)

式中：A为河道过水面积，m2；Q为流量，m3/s；t为时间，h；x为与水流方向一致的横向坐标，m；q为河道旁侧入流，m3/s；g为重力加速度，m/s2；h为水位，m。

为了推求高安城区锦河和连锦河的水面线，将对河道进行概化[20]，利用MIKE11一维水动力模型对锦河10年一遇遭遇连锦河20年一遇洪水情况进行模拟，并计算得出该工况下的洪水下水面线。将河网概化，生成河网文件，编辑河道参数(长度，断面)，输入初始条件和边界条件。

计算时间步长为0.16 h。

边界条件：锦河上游给定10年一遇的流量时间序列，连锦河上游给定20年一遇的流量时间序列，锦河下游河口位置给定水位流量关系曲线。

根据《水力计算手册(第二版)》对糙率取值要求，结合计算区域土地利用等情况，需要对锦河、连锦河一维河道模型糙率进行选取和率定。根据历史相关资料和经验，各河段糙率选取0.033。

模型断面迭代的初始水深为1.84 m。

5.2 计算结果分析

由第4节可知，锦河发生10年一遇以上洪水遭遇连锦河发生20年一遇以上洪水的概率较大，属于河道工程常见工况，水利模型构建必不可少。因此用MIKE11模型计算锦河与连锦河这种工况的洪水水面线。如表6所示。

由表6可知，当锦河出现10年一遇的洪水时，连锦河出现20年一遇情况的水位较高，这种工况的洪水同期遭遇概率相对较大，结合实际询问调查，得出连锦河河口段高水位往往是受锦河洪水顶托影响的结论，该工况下的水面线计算结果对高安市的防洪工程具有重大意义。

表6 锦河10年一遇遭遇连锦河20年一遇洪水水面线表

6 结论与展望

本文以高安市锦河与连锦河的洪峰流量资料为研究对象，采用Copula 函数建立了两水文站洪峰的同现概率分布与条件概率分布来研究干支流的洪水遭遇问题，对高安市的防洪评价工程有重要意义。得出以下4点结论：

(1)通过边缘分布函数的K-S和A-D检验，锦河和连锦河的洪峰分布服从P-Ⅲ型分布。

(2)Archimedean Copula函数的4种形式对洪峰的联合概率分布均能较好地拟合，通过优度评价准则评价后，得出拟合效果最好的函数是Frank Copula函数的结论。

(3)锦河和连锦河的洪水同现概率随着洪水的量级的增大而减小，联合概率随着洪水的量级的增大而增大。在锦河发生某一重现期的洪水情况下，连锦河发生洪水的概率随着洪水量级的增加略有上升。

(4)锦河和连锦河大量级洪水遭遇的可能性较小，而小量级洪水遭遇的几率较大，锦河和连锦河同时发生20年一遇的洪水概率为12.14%，在锦河发生10年一遇以上洪水的情况下，连锦河发生20年一遇以上洪水的概率为23.01%，并对该工况下的洪水水面线进行了计算，这对锦河流域的防洪评价等工程具有重要的实践价值。