掺硅灰的低水胶比水泥水化产物定量预测方法

陈 庆， 王 慧， 蒋正武， 曾志勇

(同济大学 先进土木工程材料教育部重点实验室，上海 201804)

水泥基材料水化进程影响其微结构的形成，是决定其性能的关键因素[1-3].浆体中各水化产物定量分析是理论预测水泥基材料微结构和性能发展的重要基础[4-6].Powers和Brownyard[7]通过大量水泥吸附解吸测试提出Power模型定量解释水泥的水化过程，孙国文等[8]提出2种C—S—H的划分，进而根据Power理论模型计算硅酸盐水泥中各水化产物体积分数，吴浪等[9]基于Power模型预测了水泥浆体的弹性模量；Jensen等[10]假定硅灰与水泥成比例反应，修正Power模型定量分析了各水化产物的体积分数(Jensen模型).而Power模型只适用于纯水泥浆体系；Jensen模型虽然考虑了硅灰的影响，但是，该模型主要适用于普通的水胶比(≥0.3)，且未考虑硅灰反应对氢氧化钙等其他组分的影响.鉴于水胶比低和胶凝组分复杂等特点，既有理论模型很难直接预测其水化产物含量.

为此，本文在简要回顾已有主要水化产物体积分数计算模型(Power模型和Jensen模型)后，基于不同水胶比下水泥水化机理和硅灰的反应机制，考虑高效减水剂、低水胶比和硅灰对水化产物的影响，修正中心粒子模型，提出掺硅灰的低水胶比水泥水化产物体积分数定量计算方法；并通过试验数据和已有模型(Power模型和Jensen模型)进行对比验证，结果表明所提模型较好地描述掺硅灰的低水胶比水泥水化进程并定量预测不同水化产物的体积含量，可为掺硅灰的低水胶比水泥微结构形成和性能演化预测提供理论支撑.

1 既有主要水化产物体积分数的计算模型

1.1 Power模型

Power模型[7]视水泥水化为水泥与水生成单一多孔凝胶固体的反应，模型可定量计算水化硅酸钙凝胶、凝胶孔、毛细水和未水化水泥的体积分数.而后研究者将Power理论模型延伸为可预测化学收缩体积分数的模型[11]，水泥水化产物的各体积分数为

凝胶：Vgs=1.5(1-p)α

(1)

凝胶孔：Vgp=0.6(1-p)α

(2)

毛细水：Vcw=p-1.3(1-p)α

(3)

化学收缩：Vcs=0.2(1-p)α

(4)

未水化水泥：Vc=(1-p)(1-α)

(5)

(6)

式中：α表示水泥水化度；ρw和ρc分别表示水和水泥的密度，g·cm-3；w和c分别表示水和水泥的质量，g.

1.2 Jensen模型

Jensen[10]假定硅灰与水泥成比例反应，考虑硅灰的掺入改进上述Power模型从而计算混凝土中各水化产物的体积分数：

凝胶：Vgs=k(1.6+0.7(s/c))(1-p)α

(7)

凝胶孔：Vgp=k(0.6+1.6(s/c))(1-p)α

(8)

毛细水：Vcw=p-k(1.4+1.6(s/c))(1-p)α

(9)

化学收缩：Vcs=k(0.2+0.7(s/c))(1-p)α

(10)

未水化水泥：Vc=k(1-p)(1-α)

(11)

未反应硅灰：Vsf=k(1.4(s/c))(1-p)(1-α)

(12)

(13)

式中：s表示硅灰的质量，g；ρSF表示硅灰的密度，g·cm-3.

2 超高性能水泥基材料水化产物定量预测方法

2.1 中心粒子模型简介

中心粒子模型假定水泥颗粒呈球形，颗粒与水立即发生水化反应，且水化产物呈球形附着于未水化水泥颗粒表面[12].水泥水化过程视为由诱导期阶段，相界面反应过程和扩散反应过程构成，则纯水泥的水化动力学方程如下[12]：

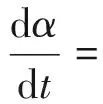
(14)

(15)

式中：Sw和S0分别表示水泥与水接触的有效表面积和总表面积，cm2·g-1；ϑ表示水与水泥质量的化学计量比(ϑ=0.25)；wg表示C—S—H凝胶中物理结合水量(wg=0.15)；Cw-free表示可用于水泥水化水的量；r0表示未水化水泥的半径，假定颗粒尺寸一致，cm；kd表示诱导期反应系数，cm·h-1；kr表示相界面反应系数，cm·h-1；De表示水通过凝胶的有效扩散系数，cm2·h-1；B和C为初始壳形成和消失的反应系数，cm·h-1；De0表示初始有效扩散系数，cm2·h-1.

2.2 掺硅灰的低水胶比水泥水化进程描述

水泥水化生成水化硅酸钙凝胶和Ca(OH)2等，掺入硅灰后，硅灰与水泥水化析出的Ca(OH)2反应形成二次水化产物，而掺硅灰的低水胶比水泥组分复杂，水胶比极低，且采用大量高效减水剂，浆体中必然存在大量未水化的水泥颗粒和硅灰，早期水化进程相对普通水泥浆体的水化进程更为错综复杂[13-14].当前中心粒子模型主要用于水胶比较高的(一般是0.3以上)浆体的水化进程模拟，尚未考虑低水胶比和高效减水剂等对水化过程等的影响，无法直接用于掺硅灰的低水胶比水泥的水化进程描述.本文基于高效减水剂、硅灰和水胶比因素的作用，修正中心粒子模型，描述掺硅灰的低水胶比水泥的水化进程.高效减水剂的掺入将延长水化诱导期，因此，本文考虑高效减水剂作用对初始壳形成速率的推迟效应修正如下[15]：

(16)

式中：XB代表减水剂对水化进程的影响系数，高效减水剂的推迟效应与减水剂的种类、水泥类型等相关，目前，量化各种类型高效减水剂的推迟效应较困难.高效减水剂的推迟效应与减水剂的种类、水泥类型等相关，量化各种类型高效减水剂的推迟效应较困难.根据已有试验数据统计分析，本文聚羧酸减水剂的修正系数取0.29[16].

硅灰的火山灰反应消耗水泥水化产生的Ca(OH)2进而影响水化进程[17-18].硅灰的水化动力学方程可表示如下[16,19]：

(17)

式中：αSF表示硅灰中二氧化硅的反应程度；mSF表示胶凝材料中硅灰的质量分数；ϑSF表示Ca(OH)2与硅灰质量的化学计量比；rSF0表示硅灰颗粒的半径，cm；krSF表示反应速率系数，cm·h-1；DeSF表示硅灰的初始有效扩散系数，cm-2·h-1；mCH(t)表示单位体积下体系中Ca(OH)2的量，其取决于水泥水化产生的Ca(OH)2量和硅灰火山灰反应消耗的Ca(OH)2量[19](α≥0.19)：

(18)

式中：γsilica表示硅灰中二氧化硅的质量分数；C0表示水泥的质量分数.

此外，硅灰的掺入引起可用于水泥水化水的量发生变化，其影响表示如下[20]：

Cw-free=

(19)

式中：r为经验参数，表示水进入内部未水化颗粒部分的难易程度；W0表示水泥的质量分数.

水胶比越低，水化产物的毛细孔隙率越低，且能提供给内部反应的水迁移至反应区越困难[21]，即水胶比越低，r值越大.已有研究表明普通水胶比下的r值为1[17]，本文考虑低水胶比对水泥水化进程的影响，分析已有试验结果量化低水胶比对水化进程的影响[14]，对r值修正如下：

(20)

式中：m表示水胶比.

2.3 水化产物体积分数定量计算方法

文献[7]假定水泥浆体由未水化部分、水化产物和孔洞三部分组成，本文定量计算含硅灰的低水胶比水泥的各水化产物体积分数时，考虑硅灰掺入后的作用，可认为硬化浆体是由以下几个部分组成[8,22]：①凝胶相，由水泥水化产生的凝胶，硅灰反应产生的凝胶和凝胶孔组成；②其他固相，包括未水化水泥，未反应硅灰和氢氧化钙(CH)组成；③孔，包括毛细水和化学收缩.

2.3.1凝胶相体积

由图1可知，凝胶相由水泥和硅灰各自反应产生的凝胶固体相和凝胶孔组成，即

Vg=Vcgs+Vsgs+Vgp

(21)

式中：Vg、Vcgs、Vsgs和Vgp分别表示总的凝胶相体积、水泥水化产生凝胶固体相体积、硅灰水化产生的凝胶固体相体积和总的凝胶孔体积，ml.

基于上述修正的中心粒子模型，水泥和硅灰水化产生凝胶固体体积分别为[16,19]：

(22)

Vsgs=3.2mSFγSFαSF/ρSF

(23)

式中：V是1 ml水化水泥的水化产物的体积，可取为2.06 ml[23]，视为主要由水化产物(C—S—H和CH[9])和凝胶孔组成；ρch表示Ca(OH)2的密度，g·cm-3(可取2.24[8]).凝胶孔所占体积视为水泥水化产生的凝胶体积的28%和硅灰火山灰反应产生的凝胶体积的19%的总和[24]，即

Vgp=0.28Vcgs+0.19Vsgs

(24)

2.3.2固相体积

如前所述，Ca(OH)2量取决于水泥水化产生的Ca(OH)2量和硅灰火山灰反应消耗的Ca(OH)2量[16].基于水泥水化程度和硅灰反应程度，未水化水泥、未反应硅灰和体系中Ca(OH)2的体积如下：

Vc=C0(1-α)/ρc

(25)

Vs=mSF(1-αSF)/ρSF

(26)

(27)

式中：Vc、Vs和Vch分别表示未水化水泥的体积、未反应硅灰的体积和Ca(OH)2的体积，ml.

2.3.3孔体积

孔体积视为由毛细水体积和化学收缩体积构成[22]，其中考虑水泥水化和硅灰反应消耗后毛细水的量及其体积表示如下[23]：

Wcw=W0-0.4αC0-0.5mSFγSFαSF

(28)

Vcw=Wcw/ρw

(29)

研究表明，水泥水化引起的收缩体积为6 ml/100 g水化水泥，硅灰反应引起的收缩体积为20 ml/100 g反应硅灰[10]，则化学收缩体积分别如下：

Vcs=0.06C0α+0.2mSFγSFαSF

(30)

式中：Vcw和Vcs分别表示毛细水的体积和化学收缩的体积，ml.

基于以上各水化产物体积的确定，各水化产物的体积分数可表示如下：

(31)

式中：Vb表示各水化产物体积的总和，ml；vi表示各水化产物的体积分数.

3 对比验证

为了验证本文所提模型的合理性，将本文模型和所提方法的计算结果和试验数据及已有模型的结果进行对比.

基于上述模型的修正和已有文献相关参数[16,23]，对比分析修正模型的模拟结果和试验结果.图1和图2分别表示不同水胶比和硅灰掺量下，本文模型Ca(OH)2量和水泥水化程度的预测结果和试验结果[22]的对比图.从图中看出，水胶比0.18，硅灰掺量20%下，Ca(OH)2含量模拟值和试验值整体相关系数约0.993 4，水泥水化程度模拟值和试验值整体相关系数约0.984 9，本文的模拟结果与掺硅灰的低水胶比水泥浆体的试验结果整体上吻合地较好.

图1 Ca(OH)2量的模拟结果和试验结果的对比

此外，本文还对比分析了提出方法预测结果和已有模型(Power模型、Jensen模型)的模拟结果.图3表示水灰比0.18下，Power模型和提出方法纯水泥水化产物体积分数预测结果的对比情况.从图中可知，不掺硅灰时，提出方法计算得到的未水化水泥以及化学收缩体积分数与Power模型结果基本一致，说明了提出方法的合理性.

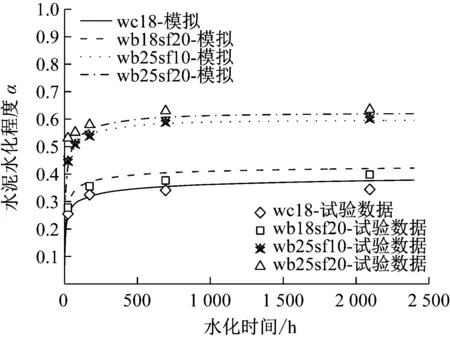
图2 水泥水化程度预测结果和试验结果的对比

Fig.2 The comparison of simulation results and experiment results of degree of hydration of cement

图3 水灰比0.18，纯水泥浆体未水化水泥和化学收缩体积分数的对比

Fig.3 Comparison of volume fraction of cement gel solid and chemical shrinkage with water to cement ratio 0.18

图4表示水胶比0.18，硅灰掺量20%时，Jensen模型和所提方法计算的毛细水体积分数的对比情况.由图可知，提出方法早期的预测结果与Jensen模型相近；后期，与Jensen模型相比，本文方法可考虑更长时间内的毛细水体积分数的变化，其结果也更符合实际情况.

图5表示水胶比0.18，硅灰掺量20%时，Jensen模型和所提方法预测的凝胶固体体积分数的对比情况和所提方法计算的水泥水化、硅灰反应分别产生的凝胶体积分数的演变.从中可知，提出方法的预测结果与Jensen模型结果整体上较吻合，与Jensen模型的结果偏差最大为8.69%.与Jensen模型相比，提出的方法还可分别定量分析水泥水化和硅灰反应产生的凝胶固体体积分数.

图6表示水胶比0.18，硅灰20%时，两种方法计算的未水化水泥体积分数的对比情况.由图可知，未水化水泥体积分数随着龄期的增加呈下降趋势，提出方法的预测结果与Jensen模型模拟结果的整体偏差不超过4.38%，进一步表明所提方法具备合理性.

图4 水胶比0.18，硅灰20%下毛细水体积分数的对比

Fig.4 Comparison of volume fraction of capillary water with water to binder ratio 0.25, silica fume 20%

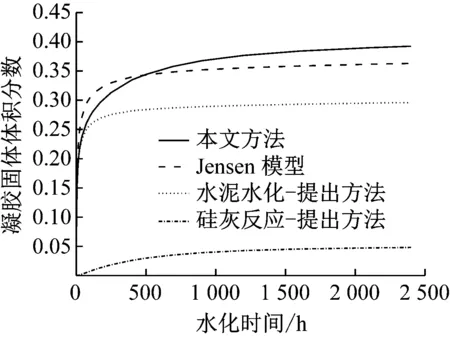
图5 水胶比0.18，硅灰20%下凝胶固体体积分数的对比

Fig.5 Comparison of volume fraction of gel solid with water to binder ratio 0.25, silica fume 20%

图6 水胶比0.18，硅灰20%下未水化水泥体积分数的对比

Fig.6 Comparison of volume fraction of unhydrous cement with water to binder ratio 0.25, silica fume 20%

4 结论

(1) 通过引入减水剂、低水胶比对水化进程的影响系数，考虑硅灰掺入对水化进程的影响，修正中心粒子模型，对低水胶比水泥的水化产物体积分数做出预测.

(2) 与试验数据对比表明，所提方法可较好地描述掺硅灰的低水胶比水泥的水化进程并定量预测不同水化产物的体积含量.

(3) 与Power 模型和Jensen模型对比，表明本文方法不仅可以较好的预测化学收缩、毛细水、凝胶固体和未水化水泥的体积含量等；同时，所提模型还可以考虑CH的体积含量，并定量预测水泥水化和硅灰火山灰反应分别产生的凝胶固体体积分数等，更符合实际情况.