一种基于改进型EMD的一维雷达距离像信号分析
程占昕 王艳娜
(1.海军大连舰艇学院信息系统系 大连 116018)(2.92677部队 大连 116018)
1 引言
一维雷达距离像是雷达目标识别领域的热点和难点问题。在距离像分析中,用什么样的特征来表达目标属性是至关重要的,高分辨距离像的特征提取和特征选择是雷达目标识别的关键环节[1~2]。一维雷达距离像根据散射点模型理论,散射点在距离单元分布可分为三种典型情况:1)距离单元内分布众多强度相当的小散射点,没有明显的特显点,这类单元的回波起伏比较小,比较稳定;2)距离单元内只包含一个特显点和众多强度弱得多的杂散射点,这类单元的回波幅度基本由特显点确定,众多弱散射点使回波幅度起伏较小,因此,这类单元回波也比较稳定;3)距离单元内包含少数几个,特别是2、3个特显点,同时也会产生较多弱散射点,当目标相对雷达转动时,特显点回波的差拍作用使引起这类距离单元回波幅度有大的起伏,特显点横距差越大,起伏越快,因此,这类单元的回波幅度随目标姿态变化起伏通常很大[3]。
与很多关于样本特征提取和特征选择方法的研究不同,本文试图从时频分析的角度对一维雷达距离像进行分析,通过分量分解以及对应的Hilbert-Huang时频谱对距离像进行一定的特征分析和探讨,力争能够从Hilbert-Huang的角度对这一领域进行尝试探讨。
2 传统的EMD分解概述
EMD的基本模式分量,称内蕴模式函数(IMF),也可看作类小波扩展[4~5]其满足如下条件:
1)整个数据序列的极值点与过零点的数量相等,或至多相差一个。
2)任一时刻,由极大值和极小值定义的信号包络均值为零。
按过零点定义信号的周期,即一个周期只包含一次基本模式的振荡,不存在复杂的叠加波,因此,IMF不限定于窄带信号,可以是幅度或频率调制信号,也可以是非平稳信号。EMD的IMF分量Hilbert变换后进行时频分析,因此EMD分解+Hilbert变换统称为Hilbert-Huang变换[6]。
对各分量进行Hilbert变换,获取时频分析,称之为Hilbert-Huang时频谱[7],如图1所示。通过下面公式求瞬时频率:

其中,z(t)是实信号 f(t)=a(t)cos[φ ( t)]的解析信号,其a(t)为IMF的瞬时幅度。由于微分法对噪声很敏感,可采用trapezoidal积分算法估计IMF的瞬时频率[8]。由图1可见,Hilbert-Huang时频谱具有很高的时频聚集性,没有交叉项,优于Wigner-Ville时频分析。
对于雷达距离像,不仅特显点幅度变化剧烈,相位以及频率等也错综复杂,而且还存在一维空间相关性。因此,EMD必须解决如下问题:
1)选取最优插值函数。目前,常用的插值函数包括径向基函数、样条插值、三次插值以及三角几何插值等。对于同一雷达距离像,采用不同的插值函数可能会得到不同的分解结果。
2)确定待插值极值点。对于一些极值点的特殊分布情况,如大宽度特显点,甚至没有或极度缺乏的极值点时,几乎所有的已有EMD方法均失效。
本文提出一种噪声辅助的EMD雷达距离像特征分析与提取方法。根据白噪声在EMD下的分解特性,把白噪声加入到信号中来补充一些缺失的尺度,进而达到更好的分解结果。
3 基于噪声辅助信号分析的改进型EMD分解
依据零均值白噪声的特性,本文提出了一种新的噪声辅助信号分析方法,定义如下:
1)在原信号 f(t)的基础上加上具有相同方差的随机零均值高斯白噪声信号nj(t)(其中j=1,2,…,J),得到辅助信号:

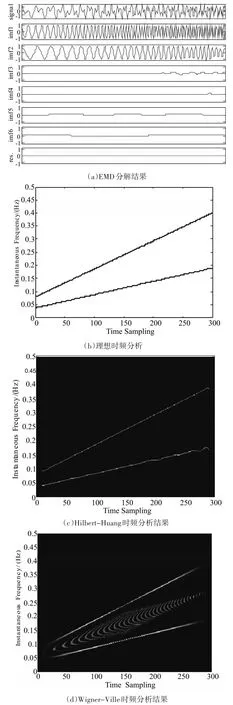
图1 两个单分量信号的EMD分解及Hilbert-Huang时频分析
2)在原信号 f(t)的基础上减去1)中的零均值高斯白噪声信号 nj(t)(其中 j=1,2,…,J),得到辅助信号:
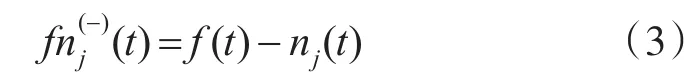
3)分别对上式中得到的辅助信号 fn(j+)(t)和fn(j-)(t)进行经验模式分解:

4)均值:
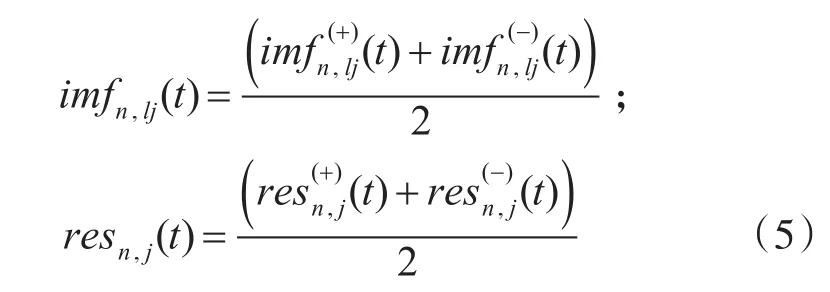
5)得到IMFs和剩余量:

6)得到:

最后,应用式ωi()t=对每个分量进行瞬时频率求解以及对应的时频谱分析。
4 基于改进型EMD的距离像性能分析
传统EMD的缺陷严重地影响了算法性能和结果。本文根据传统EMD的缺陷,提出了上述改进型EMD算法,并应用到一维雷达距离分析中去。其中主要的问题主要包括以下几方面。
4.1 IMF分量对方位敏感性分析及抑制
经验模式分解对于极值点分布比较敏感,这一点毋庸置疑,但是,同时考虑到散射点不发生MTRC的方位角范围内,目标的散射点模型基本不变[9~10]。因此,为了抑制IMF分量对方位敏感性,我们提出了分数阶相位平移下的Hilbert变换对应的分解方法:即首先把信号进行Hilbert变换获取90°相移后的信号;第二,应用分数阶角度的概念把Hilbert变换获取90°相移后的信号进行任意角度的相移,这样就可以获取0°~360°范围内任意相移下的信号。第三,对这些不同相移后的信号进行经验模式分解,然后进行反向相移。最后,把所有获取的结果进行加权求平均,即为最终结果。该方法可以有效地抑制方位敏感性,获得可靠的结果。多次试验结果证实,10到20次相移后的结果可以获取较好的效果,同时又不会增加过多计算量。
4.2 IMF分量对平移敏感性分析
经验模式分解对于极值点分布比较敏感,这一点导致了IMF分量对平移的敏感性。但是,只要各个极值点相对位置不变,IMF也就保留了稳定的特性,只要把IMF分量进行相应的逆向平移对准,所有的平移问题就可以解决[11]。
这个问题相对简单。一般来说,在进行经验模式分解前我们就可以把平移问题解决,这样经验模式分解对于平移敏感性问题就可以不用考虑。
4.3 IMF分量对强度敏感性分析
正如前述,经验模式分解最为敏感的问题是极值点分布位置(包括相对位置)以及极值点个数等等。各个IMF分量的强度大小的变化如果不足以改变极值点个数和相对位置,那么这种变化对于经验模式分解来说就不会产生IMF分量变化的敏感性(当然除了强度外)。
这一点正好与一维雷达距离像的局部能量波动相对应。很多情况下,由于各种原因,一维雷达距离像中的各个分量只是能量产生了小的波动,这种波动既没有改变主要极值点个数,也没有改变极值点相对位置,因此通过经验模式分解,IMF分量个数不会产生大变化,同时每个IMF分量对应的频率也几乎不会产生变化[12]。结果是,小的能量波动不会产生频率和个数的变化。因此,这一特性说明了在一定量的强度变化范围内,IMF没有强度敏感性。
4.4 新特征量的定义和选取
基于4.3的分析,我们可以得出结论,采用Hilbert-Huang时频谱作为特征分析不失为一种选择。但是,采用Hilbert-Huang时频谱只能够提供各个分量瞬时频率和瞬时能量的分布,因此,为了进一步有效应用各个分量的瞬时频率与瞬时能量,这里我们提出另外一个指标和Hilbert-Huang时频谱一道使用,平均瞬时频率,定义为
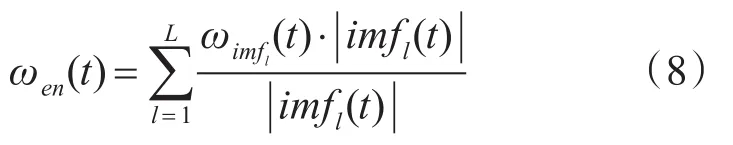
其中,L为IMF分量个数。
平均瞬时频率/能量比具有以下特性:
1)可以反应出信号的主要频率分布
假定这里只有两个IMF分量,且ωimf1(t)=100,imf1(t)=cost,ωimf2(t)=1,imf2(t)=sint,则可以得到:
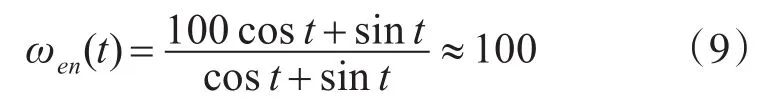
也就是说,信号的主要频率是ωimf1(t)=100,几乎可以把ωimf2(t)=1忽略不计。
2)可以获得特显点发生的主要时刻
特显点具有特别强的能量,因此,通过平均瞬时频率的求解,可以近似获取特显点对应的时刻。这种特显点的时刻估计与时域内的估计方法相比由于通过平均意义的算术运算获得的,因而具有更强的鲁棒性。同时,也告诉我们,特显点除了在时域内估计外,还可以通过时频分析进行估计。这种方法补充了特显点的估计方法,充实了特征提取的内容,增加了工程可靠性。
3)可以获得主要特显点发生的个数
由于特显点具有特别强的能量,因此,每一个特显点必然对应一个大的凹点或者凸点,通过对这种变化剧烈的凹凸点进行统计,就会近似获取特显点的个数。这种特显点的个数估计与时域内的估计方法相比由于通过平均意义的算术运算获得的,因而同样具有较强的鲁棒性。同时,特显点个数除了在时域内估计外,还可以通过时频分析进行估计。这种方法补充了特显点的个数估计方法,充实了特征提取的内容,同样会增加工程的可靠性。
5 结语
本文提出了一种改进型EMD分解算法并把其应用于一维雷达距离像的数据分析中。改进型EMD分解算法克服了传统EMD分解算法的一些主要缺陷,可以更好地对非线性、时变信号进行分析。结合一维雷达距离像的特点,提出了平均瞬时频率和Hilbert-Huang时频谱结合应用的试验分析,该种方法在一维雷达距离像分析中具有重大的潜力。

