滑动平均的灰色理论在油管腐蚀速度中的应用

张 锐.

(中石化石油工程设计有限公司，山东东营 257000)

某气藏已开发至中期，大都气、水同产，且气、液中含H2S、CO2等腐蚀介质。它们溶于水后形成弱酸，对井下管柱具有极强的腐蚀性，不仅影响了油气井的正常作业，降低了油管的使用期限，而且给修井作业带来不必要的麻烦。大量的现场经验表明，含H2S、CO2共存时的腐蚀行为远比它们单独作用时复杂的多。由于不同区块CO2和H2S含量各不相同，井下腐蚀环境各异，即使在相同的区块，井下油管的腐蚀状况也会存在差别，因此，有效地开展预测油管腐蚀速度及其影响因素和相互作用关系的科学研究，对预测油管使用寿命，保证气井的安全生产，降低修井成本，具有重要意义。

气井井下油管腐蚀是一个复杂的体系，腐蚀速度也是由各种影响因素相互作用、共同影响的，它不但与腐蚀介质浓度及分压因素有关，而且与环境条件、油管材质及产水量等有关。由于各影响因素具有随机性和不确定性，因而，用简单的数理模型来表达各影响因素与腐蚀速度之间对应的关系是不切实际的。像这种具有模糊性和复杂性的腐蚀速度的预测问题，可以把井下管柱的腐蚀看成是灰色系统，通过使用滑动平均法对传统的灰色模型进行优化，结果表明具有很好的适用性。

1 滑动平均的灰色预测的原理及方法

(1)确定需要预测的灰色系统中，某项指标在连续若干个时间内按顺序排列的原始数列。X(0)=[X(0)(1),X(0)(2),X(0)(3),…,X(0)(n)]

(2)采用滑动平均法处理原始数列。

滑动平均法的计算公式为：

(1)

两端点的计算公式为：

(2)

(3)

(3)累加生成1-AGO序列。

经滑动平均法计算后，将所得的新序列作一次累加处理，得到X′(0)的1-AGO序列X(1)。

i=1,2,…,n

X(1)=[x(1)(1),x(1)(2),…,x(1)(n)]

=[x′(0)(1),x′(0)(1)+x′(0)(2),…,x′(0)(1)

+…+x′(0)(n)]

(4)

(4)将累加后的数列X(1)用微分方程(5)近似表示。

(5)

其中a为发展灰数，u为内生控制灰数。

(5)构造向量Yn和矩阵B。

Yn=[x(0)(2),x(0)(3),…,x(0)(n)]T

(6)

(7)

(8)

(7)确定模型。

(9)

(8)对计算所得的拟合值进行一次累减处理，得到1-IAGO序列，得到原始数据的还原值。

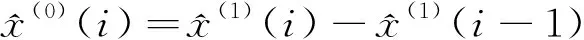
(10)

2 模型精度检验

灰色系统理论有三种模型精度检验方法，分别为：残差检验、关联度检验和后验差检验。

(1)残差检验。

残差检验包括绝对误差检验和相对误差检验。

绝对误差：

(11)

相对误差：

(12)

(2)关联度检验。

分别计算原始数据还原值与其真实值之间绝对误差的绝对值，比较得出其最小值和最大值：

(13)

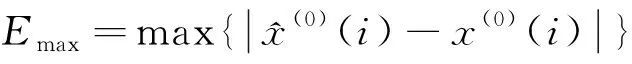
(14)

计算关联系数w(i)：

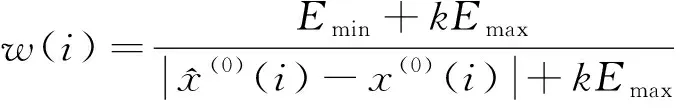
(15)

k为分辨系数，一般取0.5。

关联度R计算：

(16)

检验标准：k=0.5时，R>0.6有意义。

(3)后验差检验。

原始数列的均值：

(17)

残差均值：

(18)

原始数列的方差：

(19)

残差的方差：

(20)

后验差比值C：

(21)

小误差概率P：

(22)

(4)精度等级。

按照上面两个指标，可以将预测精度划分为四个等级，等级划分如表1所示:

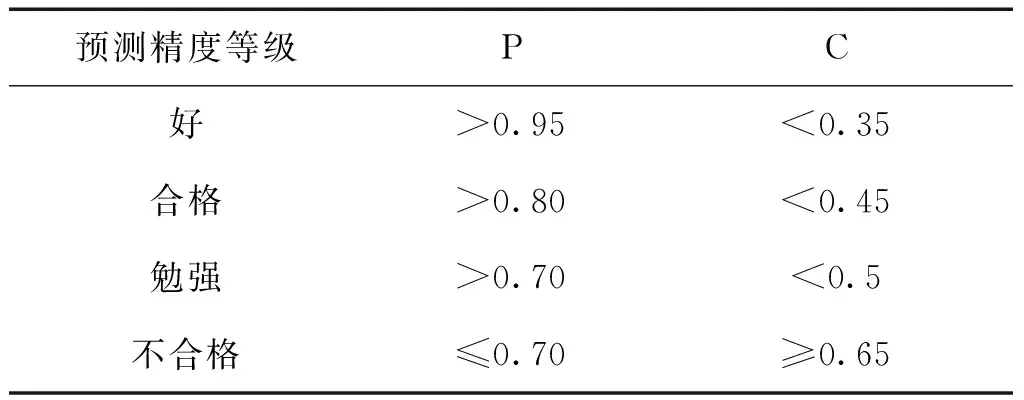
表1 预测精度等级划分Table 1 Classification of prediction accuracy

3 实例应用

高温、气液混输和天然气中普遍含CO2、H2S是某气田生产腐蚀环境的主要特点，由此产生的腐蚀问题较为严重。该气田由于井下油管投运时间长，井下流体腐蚀性强，导致井下油套管腐蚀严重，影响气井生产和修井作业,部分油管腐蚀严重导致气井修死。M气井为中度腐蚀的一口井，采用光油管完井，即油套环空连通，对套管采用多臂井径仪检测发现在741米井段腐蚀变形。

为了真实可靠地评价井下的腐蚀状态，解决井下挂片检测实施的不便性、局限性和与真实腐蚀状态的误差性，采用了CFL-1动态腐蚀试验环道装置进行实验研究，该装置操作方便，真实可靠，大大降低了腐蚀检测成本，减少作业，为安全生产提供指导。根据M井的温度、压力、流速等参数确定出M井最近七年的腐蚀速度，如表2所示。

(1)原始数列为:

X(0)=[0.262,0.247,0.217,0.183,0.157,0.142,0.131]利用滑动平均法对原始数据进行处理,得到的滑动平均序列为：X′(0)=[0.25825,0.24325,0.216,0.185,0.15975,0.143,0.13375]经滑动平均处理进行一次累加后得到的新序列X′(0)：X(1)=[0.25825,0.5015,0.7175,0.9025,1.06225,1.20525,1.339]

表2 某气田M井最近七年的腐蚀速度实测值Table 2 Measured corrosion rates of M well in a gas field in the last seven years

(2)参数估计并构造预测模型。

用最小二乘法解得：

则对应的时间响应函数，即预测模型为：

X(1)(k+1)=2.194074-1.935824e-0.135k

(3)累减还原预测结果。

(4)计算相对误差。

q(i)=[-0.0145,-0.0102,-0.0159,0.0193,0.0368,0.0035,-0.0522]K取0.5时，计算得到关联度R=0.79，满足R>0.6的检验标准。

(5)后验差检验。

残差均值：ξ(0)=0.02177

原始数列的方差：S12=0.002679

残差的方差：S22=0.000285

后验差比值C：C=0.326

计算得出0.6745S1=0.03491，由表3可以看出i=1,2，……，7时，|ξ(0)(i)-`ξ(0)|的值均小于0.6745S1，所以P值为1。

(6)模型精度检验。

以某气田M井最近七年测得的腐蚀速度为研究对象，对七年的腐蚀速度进行拟合，拟合情况如表4所示：

表3 |ξ(0)(i)-ξ(0)|值的求解Table 3 The solution of |ξ(0)(i)-ξ(0)|

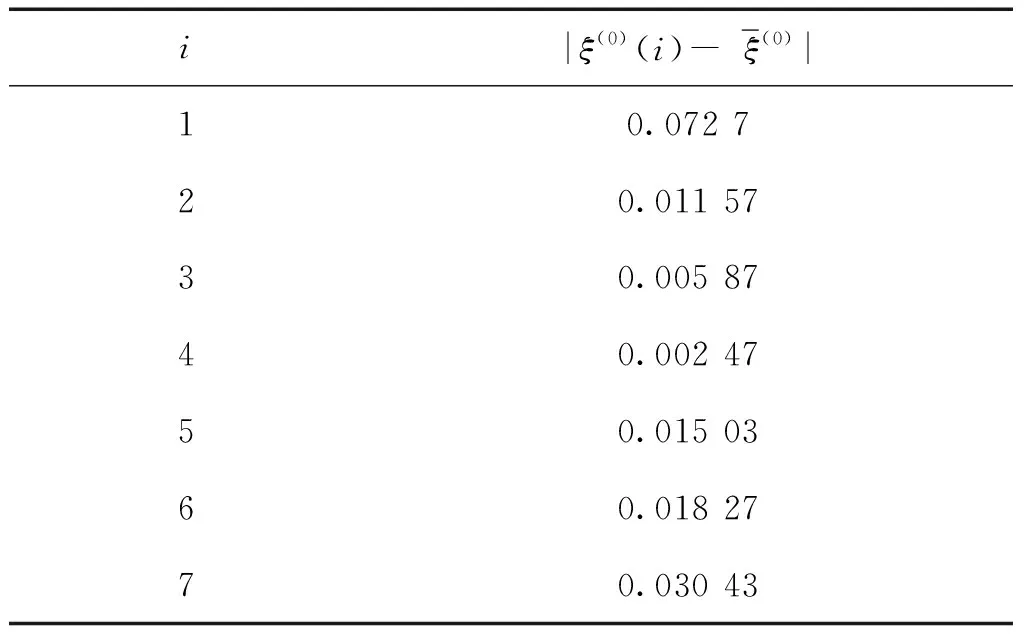
表3 |ξ(0)(i)-ξ(0)|值的求解Table 3 The solution of |ξ(0)(i)-ξ(0)|

i|ξ(0)(i)-ξ(0)|10.072 720.011 5730.005 8740.002 4750.015 0360.018 2770.030 43

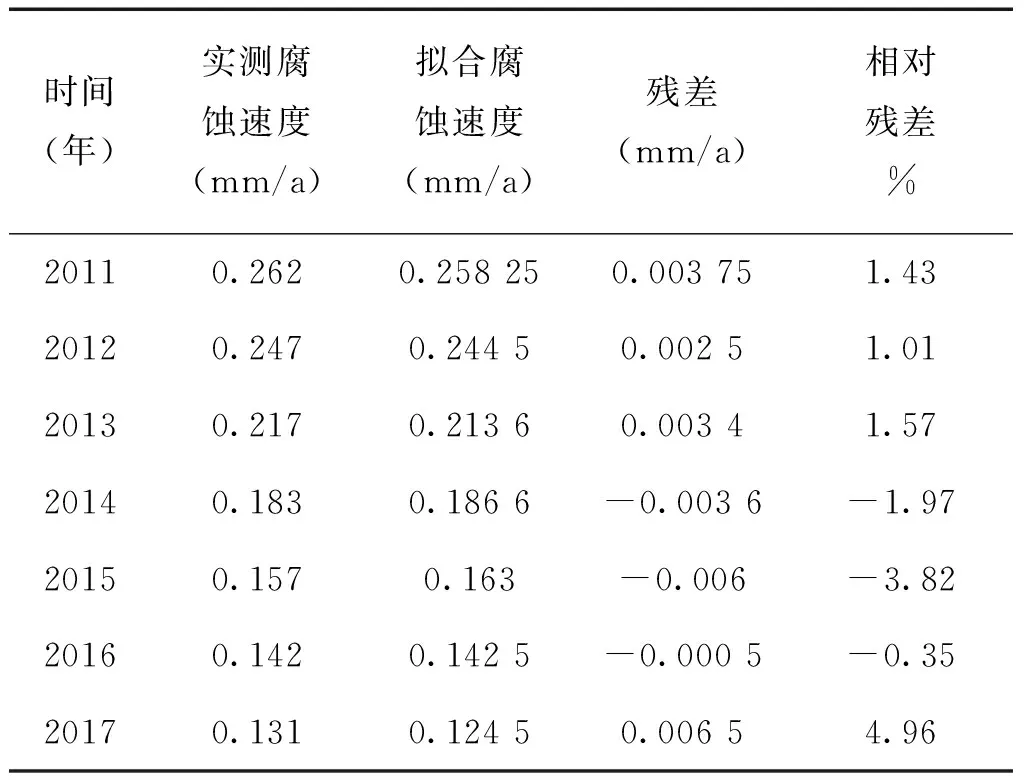
表4 拟合值和实际测量值、残差和相对残差Table 4 Fitting values , actual measured values, residuals and relative residuals

根据预测精度等级划分结果表3可知，此滑动平均的灰色预测模型的预测精度等级为好。且由表4可见，实际测量值和拟合值很接近，残差和相对残差都较小，相对误差控制在5%以内，具有较高的拟合精度。因此，可以用该模型对该气田M井未来五年的腐蚀速度进行预测。预测结果如表5所示。

4 结论

(1)针对井下油管腐蚀问题，提出了滑动平均的灰色理论预测模型，为井下腐蚀监测提供依据，是处理油管腐蚀速度预测问题的有效工具。

(2)根据M井最近七年的油管腐蚀速度实测值，建立油管腐蚀预测模型，经验证，该模型的预测精度等级为好(小误差概率P=1>0.95，后验差比值C=0.325<0.35)，预测精度控制在5%以内。

表5 气田M井未来五年腐蚀速度的预测值Table 5 Predicted corrosion rate of M well in gas field in the next five years

(3)建立的油管腐蚀速度预测模型随时间呈指数函数变化，并预测得出M井未来五年的油管腐蚀速度分别为0.108 8 mm/s，0.094 5 mm/s，0.083 mm/s，0.072 5 mm/s，0.063 4 mm/s。

(4)推广该模型用于油管腐蚀预测，可根据反馈的数据制定更为有效的防腐措施，或为油管的更换使用提供指导作用。