柔性管节点对海洋导管架固定平台非线性分析的影响*

刘东亮 黄怀州 阮胜福 陈 鹏

(海洋石油工程股份有限公司 天津 300451)

圆管桁架结构具有受力各向一致性、抗扭转能力强及可焊性优良等优点，是海上固定平台的主要结构形式，其中的管节点模拟目前主要采用线弹性分析法[1]，该方法将整个结构系统看成一个线弹性传力系统。

早期的线弹性传力系统研究方法假定管节点完全刚性固结，而实际上所有的节点(尤其是钢结构节点)都存在一定的柔性，是介于刚性连接与铰接之间的柔性连接。为了简化计算，早期线弹性分析中采取的理想假定不能反映节点的实际力学特征[2-4]。前人对节点的柔性行为进行了研究，文献[5]提出了一套表征管节点线弹性柔性的刚度方程；文献[6]使用有限元法对单个管节点进行了模拟，研究了其对平台结构响应的影响；文献[7]提出了一种半解析法，对海洋平台T、Y型管节点的局部柔度进行了分析；文献[8]提出了一种在有限元分析中反映管节点柔性的单元，该单元可有效地反映管节点在轴力和弯矩作用下的局部变形特性，并导出了T型、Y型以及K型管节点的局部柔度等效单元的刚度矩阵。然而，上述研究成果主要侧重于管节点的线弹性柔性行为。

随着海洋工程相关规范的逐步完善，尤其是API RP 2A 22版[9-10]的逐步采用，固定平台的非线性分析将得到逐步推广。文献[11]基于结构非线性对导管架平台进行了整体的非线性分析，也证明了非线性分析的应用价值。在非线性分析进程中，当管节点产生非线性行为时上述关于线弹性管节点的研究成果将不完全适用。从20世纪90年代开始，一项由BP、SHELL等9家国际石油公司发起，由MSL Engineering Limited具体组织实施的管节点非线性行为研究工程持续开展，期间通过有限元法和大量实验室标定，并经过两个阶段的研究，在2000年发表了一项名为MSL非线性管节点柔性方程的成果[12]。目前国际范围内非线性分析的主要分析工具如USFOS、CABFOS等均引入了MSL公式作为管节点非线性分析的可选项，因此在工程应用研究时是否应该考虑MSL节点非线性柔性具有重要的意义。

本文基于前人成果，引入MSL非线性柔性管节点模型，研究了柔性管节点对导管架固定平台非线性分析的影响，结果表明考虑管节点柔性进行非线性分析时，海上固定平台的局部和整体刚度均得到了显著降低，进而影响了非线性强度分析结果及平台设计的经济性。

1 MSL非线性柔性管节点模型

管节点受力时将发生局部弹塑性变形，但传统的刚性节点连接方式假定管节点在受力分析时不考虑受力后自身的局部弹性变形以及屈服后的塑性变形等柔性行为。MSL柔性管节点模拟方式是在弦杆表皮和弦杆中心线之间虚拟一个非线性弹簧来模拟管节点受力后的非线性变形(图1)。

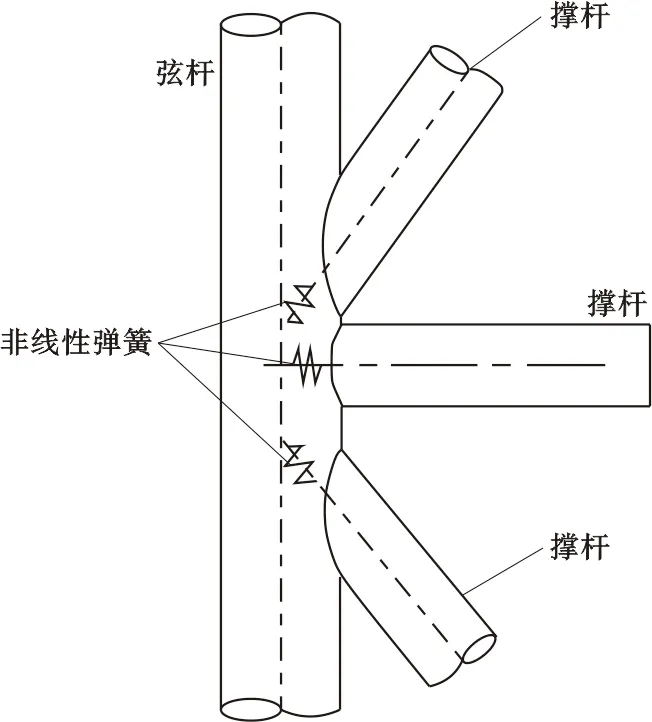
图1 MSL柔性管节点模型Fig.1 Models of MSL flexible tubular joint

非线性弹簧的刚度即MSL非线性管节点柔性方程为[12]

(1)

(2)

Φ=pchar/pu

(3)

式(1)～(3)中：p为拉筋轴向力，kN；m为拉筋弯矩，kN·mm；pu为管节点轴向许用力均值，kN；mu为管节点许用弯矩均值,kN·mm；Φ为强度系数；pchar为管节点设计标准确定的轴向许用力,kN；Fy为材料屈服强度，MPa；δ为管节点变形，mm；θ为管节点拉筋转角，rad；Qf为弦杆受力后的能力折减系数对应pchar设计标准；D为节点外径，mm；A为无量纲常数，对应管节点类型(K、Y、T)和外形尺寸的参数；B为尺寸常数，MPa,对应管节点类型(K、Y、T)和外形尺寸的参数。

式(1)为管节点轴向受力和轴向变形的关系式，式(2)为管节点承受弯矩和撑杆旋转角度的关系式。式(1)、(2)为典型的非线性方程，简称MSL公式，为管节点受力后从线弹性阶段直至屈服阶段整个过程的非线性行为的数值表达，在工程应用时依据管节点的几何参数及受力情况不断修正公式中的参数值，以完整准确模拟管节点局部非线性柔性行为。

2 实例计算

2.1 计算方法

研究MSL非线性柔性节点模型对固定平台非线性分析的影响，其主要计算步骤如下：

1) 为直接体现MSL非线性柔性节点模型对管节点的影响，直接对典型Y型节点连续施加弯矩，并将分析结果与刚性固结节点比较；

2) 为体现MSL柔性节点模型对静态非线性分析的影响，对二维框架结构进行倒塌分析，并将分析结果与刚性节点比较；

3) 为体现MSL柔性节点模型对平台整体动力响应的影响，对实际三维固定平台进行模态分析和非线性动力地震时程分析，并将分析结果与刚性节点比较。

以上分析使用专业非线性分析工具USFOS分析程序，其可同时兼容MSL柔性节点模型和普通刚性节点模型。

2.2 管节点直接非线性加载分析

基于Y型管节点受力分析模型的相关参数(表1),对Y型管节点进行加载分析。外力施加于撑杆端部，按照步步累积加载方式持续加载，每次增加140 kN直至管节点发生屈服。加载结束后处理模型，提取每次加载后撑杆端部的受力及竖向位移并绘制曲线(图2)。传统刚性管节点模型和MSL非线性柔性节点模型均采用上述加载方式。

由图2可以看出，施加相同荷载时，MSL柔性管节点模型受力后撑杆的变形更大；与此对应的是,产生相同的变形，MSL柔性管节点模型比传统刚性管节点需要更小的外力，说明MSL柔性节点模型的局部刚度更小，而且这种差异在达到材料屈服后更加明显。

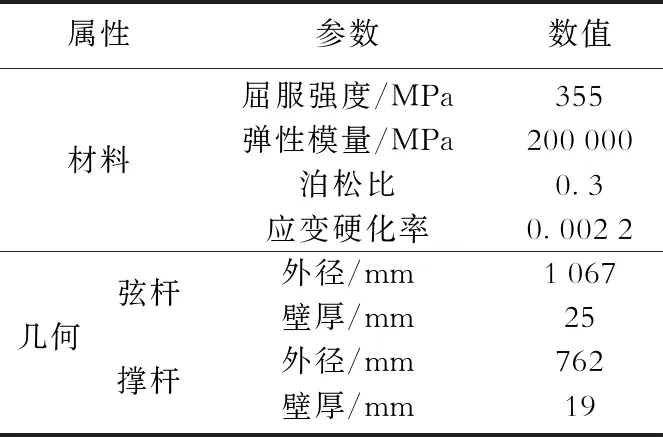
表1 Y型管节点受力分析模型材料和几何属性Table 1 Model material and geometric properties of class-Y tubular joint

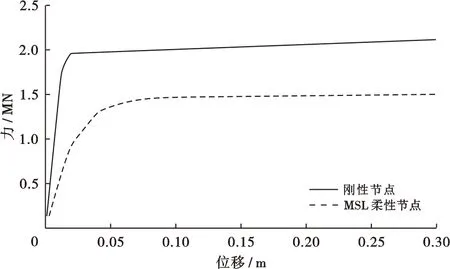
图2 Y型管节点受力分析结果Fig.2 Loading analysis results of class-Y tubular joint

2.3 静力倒塌分析

为研究MSL柔性管节点模型对静态非线性分析的影响，进行静态倒塌分析(图3)。为使分析结果明了清晰，使用简化二维框架模型进行分析(图3a)。受力点连续施加推力F，按照步步累积加载的方式持续加载，每次增加10 kN直至二维框架结构发生失稳(图3b)。提取每次加载后加载位置的受力及横向位移并绘制曲线(图4)。传统刚性管节点模型和MSL柔性节点模型均采用上述相同加载方式。由图4可以看出，施加相同的外力后，考虑MSL柔性管节点的模型和传统刚性模型相比会有更大的整体变形;与传统的刚性管节点模型相比，MSL柔性管节点模型将更早发生失稳。

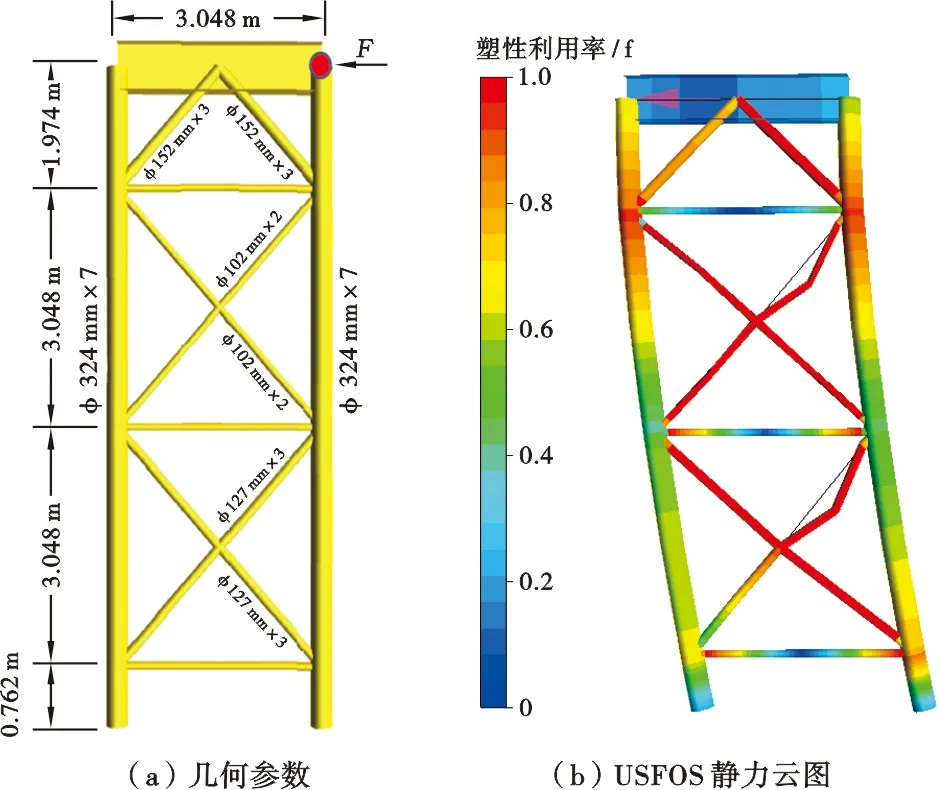
图3 Y型管节点二维框架静力倒塌分析模型Fig.3 Static collapse analysis model of 2-D frame of class-Y tubular joint

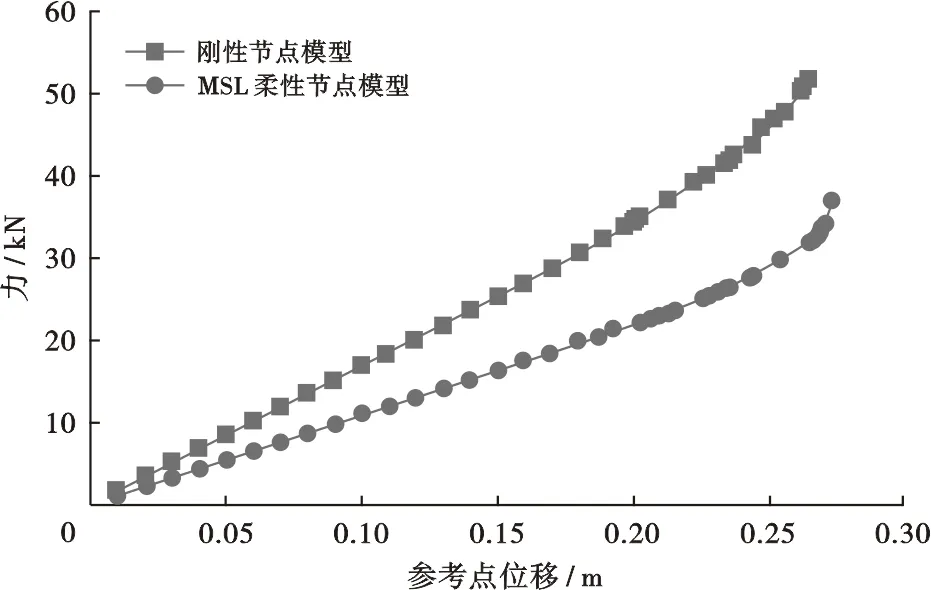
图4 Y型管节点二维框架静力倒塌分析结果对比Fig.4 Comparison of static collapse analysis results for 2-D frame of class-Y tubular joint

2.4 动力模态分析

结构自振周期是结构动力分析的关键属性，自振周期计算错误将会得出错误的动力响应计算结果，从而影响结构或构件的安全[13]。对X平台(表2)采用MSL柔性节点模型和传统刚性节点模型分别进行模态分析，结果表明使用MSL柔性节点模型的平台自振周期更长，最大相差11.51%(表3)。

多自由度振动方程为

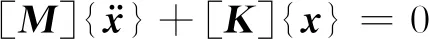
(4)

该方程若有解,须满足

|([K]-ω2[M])|=0

(5)

式(4)、(5)中：[M]为系统质量矩阵；ω为自振频率，Hz；{x} 为阵型向量；[K]为系统刚度阵。

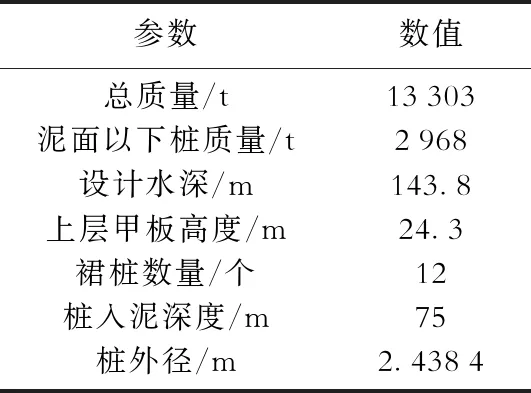
表2 X平台参数Table 2 X platform parameters

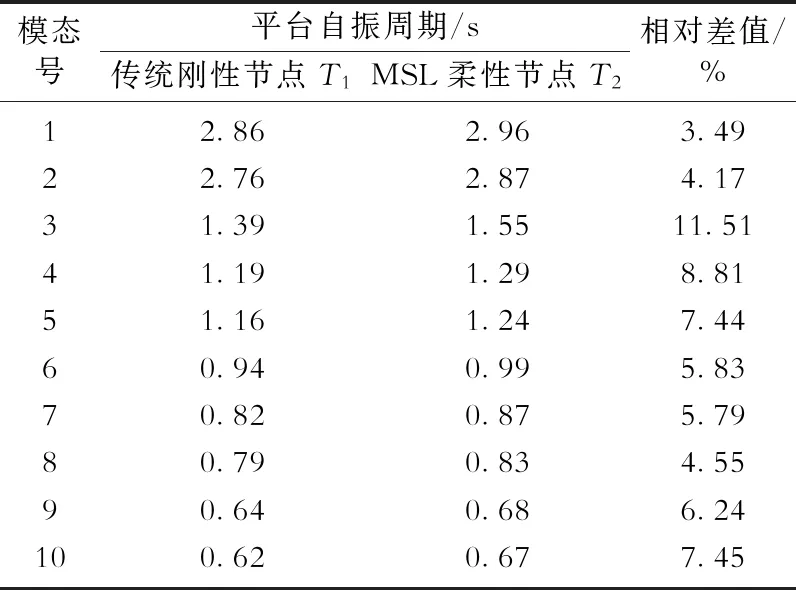
表3 X平台自振周期分析结果Table 3 Natural periods of vibration of X platform

显然MSL柔性管节点较传统刚性管节点降低了平台的整体刚度，从而导致MSL柔性节点模型具有较大的自振周期，进而对动力分析造成影响。

2.5 动力响应分析

为进一步具体研究MSL柔性管节点模型对平台动力分析的影响程度，使用Lzmit三维加速度时程(图5)对X固定平台进行非线性地震时程分析。

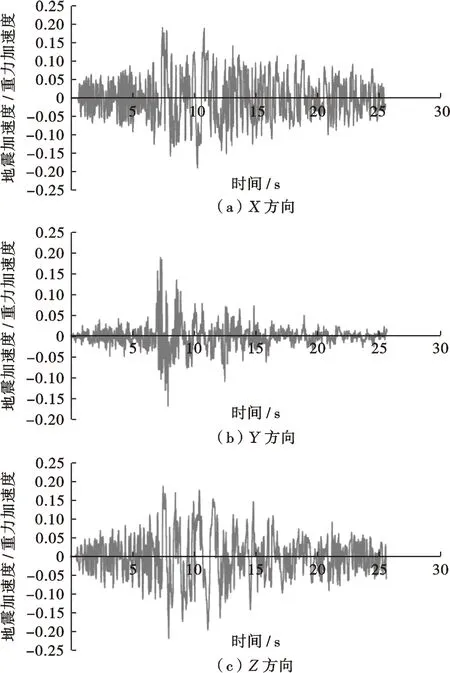
图5 X平台Lzmit三维加速度时程输入Fig.5 Lzmit 3-D acceleration time history input of X platform

对分析后处理模型提取平台基底剪力响应时程、倾覆力矩响应时程、能量吸收时程，并进行对比分析(图6)。由图6可以看出， MSL柔性管节点模型的地震响应基底剪力和倾覆力矩均较小，但具备更大的能量吸收能力。

由X平台Lzmit时程对应的地震反应谱(图7)可以看出：当自振周期大于1 s时，随着自振周期的增大，地震响应加速度变小，这进一步说明MSL柔性节点模型的更小基底剪力和倾覆力矩是源于整体刚度变小和自振周期变大。整体动力分析表明，在非线性极限强度分析中，使用MSL柔性节点分析的模型分析结果显示更大的强度储备能力，承受循环荷载时能吸收更多的能量，具备更大的结构冗余度，这将在实际工程应用中带来巨大的经济效益。

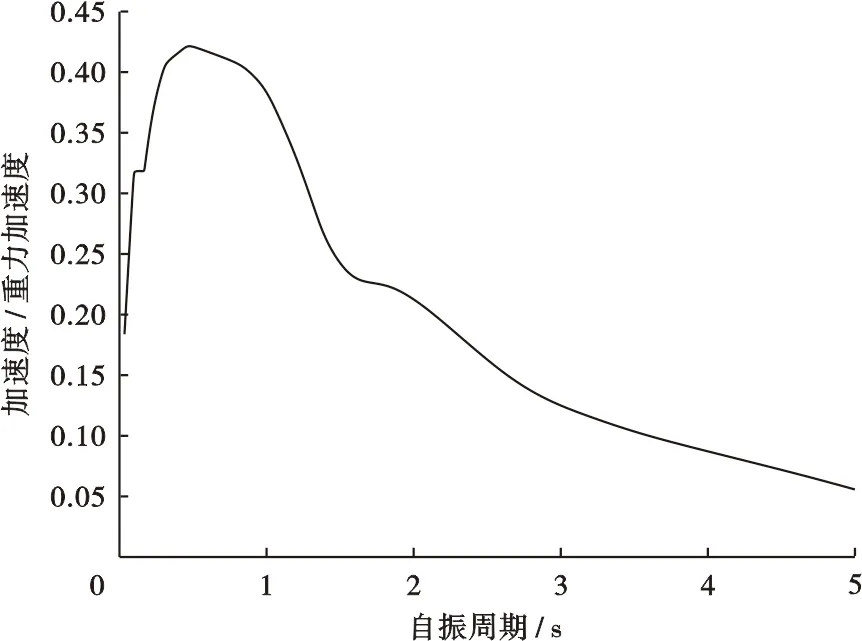
图7 X平台Lzmit时程对应的地震反应谱Fig.7 Seismic response spectrum corresponding to Lzmit time history of X plarform

3 结论

1) 当考虑MSL柔性管节点时，导管架固定平台非线性动态和静态分析结果与使用传统刚性节点的分析结果均存在差别，表现为静力倒塌分析时在相同外力作用下结构整体更容易发生变形；动力分析时结构主要的自振周期变大，地震响应基底剪力，倾覆力矩均较小，具备更大的能量吸收能力。

2) MSL非线性柔性管节点模型的引入导致导管架固定平台非线性分析结果产生差异的原因是管节点柔性降低了结构的整体刚度，刚度的减小可使一些动力分析如地震分析工作中减少不必要的结构加强，带来巨大的经济效益。

3) 鉴于管节点柔性的客观存在及其在非线性分析中的重要影响，建议在海洋导管架固定平台非线性分析中引入MSL公式模拟管节点的非线性行为。