南海高温高压气井外部温度场建立与井底压力计算*
郑永建 曾 桃 李跃林 白坤森 熊 钰
(1.中海石油(中国)有限公司湛江分公司 广东湛江 524057; 2.西南石油大学石油工程学院 四川成都 610500)
1 问题的提出
位于莺歌海海域的东方13-1气田是南海比较典型的高温高压气藏,其地层压力系数为1.90~1.94,地层温度为138~143 ℃,井型大多为大斜度井或水平井。由于该气藏压力、温度均较高和储层物性较好,气井(本文指南海HTHP气井)产能较高,开井生产过程中井口温度也较高。
受高温高压的影响,钢丝测压成本相对较高;同时受复杂井眼轨迹的制约,井下工具的通过性也得不到保障。因此,如能实现用井口测压的方式代替井下测压,对降低作业成本与提高动态监测频率都有重大意义。但实际上若要使用井口测压的方式进行资料分析,面临着以下难题。
1) 采用推算的井底压力进行产能解释时常得到异常产能曲线,这在东方13-1气田表现得尤其明显,同批的F1—F5共5口气井的产能曲线均呈现出二项式拟合斜率为负、指数式拟合指数大于1的异常情况(以F1井为例,其实测产能测试曲线如图1所示)。由于5口气井产能较高且产水很少,该异常与气井由于携液能力不足导致积液而使得测试曲线异常[1]不同,主要与井底压力推算结果受温度影响导致的多种扰动有关[2]。
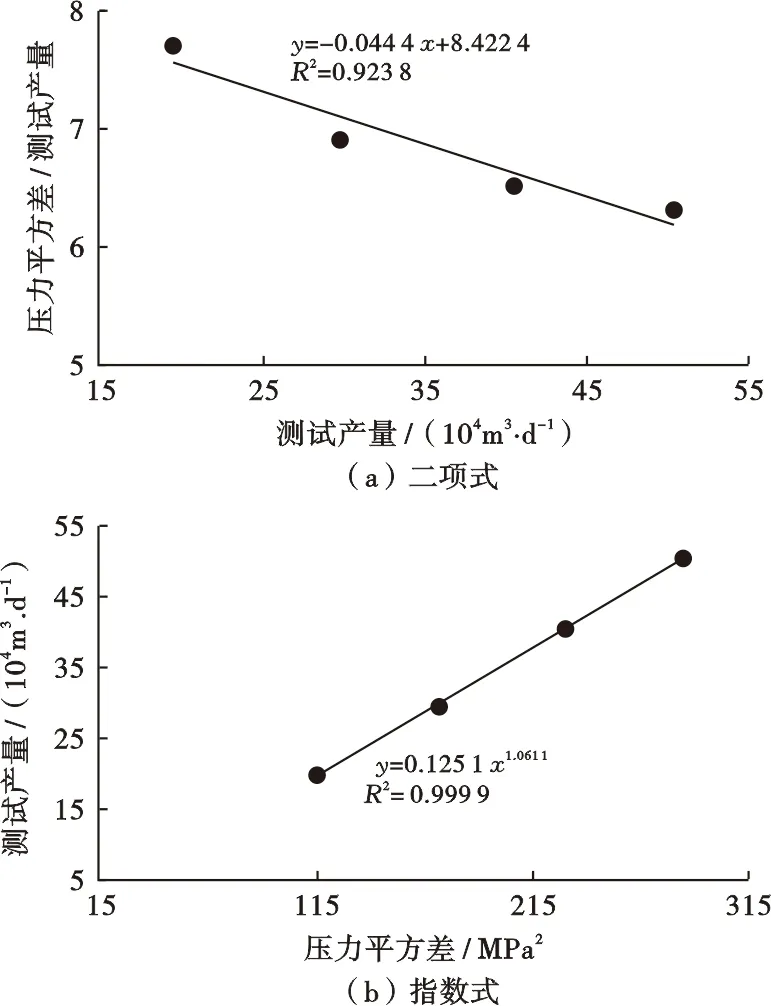
图1 东方13-1气田F1井实测产能曲线Fig.1 Productivity curve of Well F1 in DF 13-1 gas field
2) 东方13-1气田气井开井井口温度高达90 ℃左右,而关井期的井口压力是逐渐下降的;现场测试往往持续3~5 d,后期井口温度基本上随大气波动,井底压力的准确计算显然同样受到温度扰动影响。因此,开井井底压力和关井恢复井底压力精确计算都首先需要进行气井外部温度场的准确描述。
近年来多名学者在海上气井井筒传热问题研究上取得了不少进展[3-8]。宋洵成 等[3]基于深水钻井液循环时井筒与地层和海水的传热机理,建立了全瞬态深水钻井液循环温度计算模型,但建立传热方程的基本假设为保温层外壁面与海水对流换热量等于外壁面与保温层的热传导换热量,不仅没有考虑海水上的隔水管段,也没有考虑海水的分层特性影响。刘通 等[4-5]对大气段、海水段、地层段分层给出套管外壁与外界环境间的总传热系数,采用龙格库塔法耦合求解温度梯度方程和压力梯度方程,虽然考虑了海水的分层特性,但测试期间海水温度场取为定值,而且没有对海水温度场在测试期间的短期变化和四季中的长期变化进行说明,这样处理对于需要采用井口压力计算井底压力后再进行试井解释的精度要求相差较远。针对以往模型中缺乏低温海水对流换热系数的实验关系式以及忽略了气液两相流不同流型下流动时的传热规律存在较大差异问题,马永乾[6]利用模拟深水条件的气液两相流传热系统进行了传热实验研究,结果表明深水低温条件下层流时流速对于传热的影响非常明显,并给出了模拟深水下的对流换热计算公式,但对于关井时的瞬态问题没有进行处理,这对计算压力恢复早期数据影响很大。在以往的井筒温度压力剖面计算中,主要集中于海水段、大气段以及地层段传热模型的建立,而没有将井口装置传热耦合进来,也没有对海水的分层特性以及对受洋流与辐射传热影响较大的海水温度场的变化进行模型建立及参数取值详细说明。与陆上模型不同的是,由于海上测试作业受天气影响较为严重,强制对流换热与辐射换热比陆上更为强烈,导致井口装置、大气段和海水段的换热显著强于地层段。对于东方13-1气田这类关井初期井口温度达到近100 ℃的高温高压气井而言,大气和海水温度变化对计算结果的影响则更为明显。因此,建立从井口到井底的完整传热模型既是确保物理模型合理可靠的需要,也是井底压力准确计算的保证;只有把每个环节都考虑得更为精细,才能使利用井口压力恢复数据计算的井底压力数据符合试井解释的精度要求。
本文结合传热模型,采用温度-压力耦合计算方法,对大气段、海水段、泥线下地层段分别建立了气井井筒外部温度场与传热模型,计算分析了南海高温高压气井的井底流压和静压。该模型产能测试井底压力计算数据的误差在5‰以内,解决了产能测试曲线为负的问题;而且利用关井井口压力计算所得井底恢复压力平均误差仅为0.617‰,能够满足试井分析的精度要求。
2 井筒外部温度场与传热模型的建立
2.1 油管头的外部温度场及传热模型
在海平面以上,油气井外部可划分为隔水管和油管挂以上的井口装置两部分。气井的井口传感器一般安装在生产翼阀和油嘴之间,只能测量生产过程中的嘴前压力,翼阀关闭后井口压力值由采气树树帽处安装的压力传感器提供。由于采气树顶端处流体是不流动的,虽然对井筒压力测量的影响可以忽略不计,但对高温高压气井而言,采气树顶端温度可能与流通通道内温度产生近10 ℃的温差,导致无法直接用于关井井筒温度剖面的计算,在实际应用计算过程中只能根据开井时测得的气体流动温度推演关井时的井筒温度变化。该段的外部温度场即为大气温度,测试期间气井井口装置外部的大气温度场受气温影响会存在周期性变化,主要是早8点以后气温逐渐升高,下午4点左右为温度最高点,而后气温逐渐下降,第2天早7点左右达到最低点。因此,海平面以上的井口装置的传热过程为井筒内流体向井口装置传热和井口装置向大气传热,向大气传热存在对流和辐射传热2种。2种传热在引起油管头内流体的温度变化是一致的,因此可考虑海平面以上的外部温度传热系数kair为对流传热系数和辐射传热系数之和。
由于井口装置带有翼阀,可分为垂直管段、带翼阀管段和水平支管。
当考虑油管挂和油管头测点之间的能量平衡时,可建立如下的能量守恒方程,即井口装置的总传热方程为[9]
(1)
式(1)中:Tim为井口装置入口截面上的流体温度,K;Tom为井口装置出口截面上的流体温度,K;Qr、Qrm、Qrmm为各垂直管段、各水平支管、各个带水平支管段的垂直管段的散热量,W/m;wg为气体质量流量,kg/s;cg为气体比热容,J/(kg·K)。
2.2 隔水管外大气段和海水温度场及井筒传热模型
在海上,由于隔水管外风流和洋流的存在对隔水管传热影响很大,细分其外部温度场是高精度计算井底压力的基本条件之一。隔水管外大气段的外部温度场视为当地大气条件,海平面至泥线段的隔水管井筒段向外传热时,其外部温度场为海水的垂向温度分布场。实际上,海水的垂向温度分布分为表层、混合层、斜温层(温跃层)和深水层温度分布[10],如图2所示。

图2 海水垂向温度分布示意图[10]Fig.2 Diagram of vertical temperature distribution in seawater[10]
因此,分段建立隔水管外部海水温度场,以方便建立从油管内流体通过油管、套管、保护液和隔水管向外传热的总方程。
2.2.1海水温度场计算模型
1) 表层温度随季节变化计算。
海水表层温度是建立海水温度的基础之一,是垂向涡动传热的基础,因此首先需要建立海水表层温度预测模型。我国南海海域海水表层温度主要取决于太阳辐射的分布[11],此外因海湾所处的地理环境的不同,海岸形态、海湾孤立程度,尤其是气象因素的影响,使得海湾表层水温的地理分布较为复杂且因季节变化而异。南海沿岸诸湾的平均表层水温从汕头港到莺歌海约为21.1~26.7 ℃[12]。为此,由实测温度数据(图3)回归得到了不同月份莺歌海海水表层温度随季节变化的关系式,即
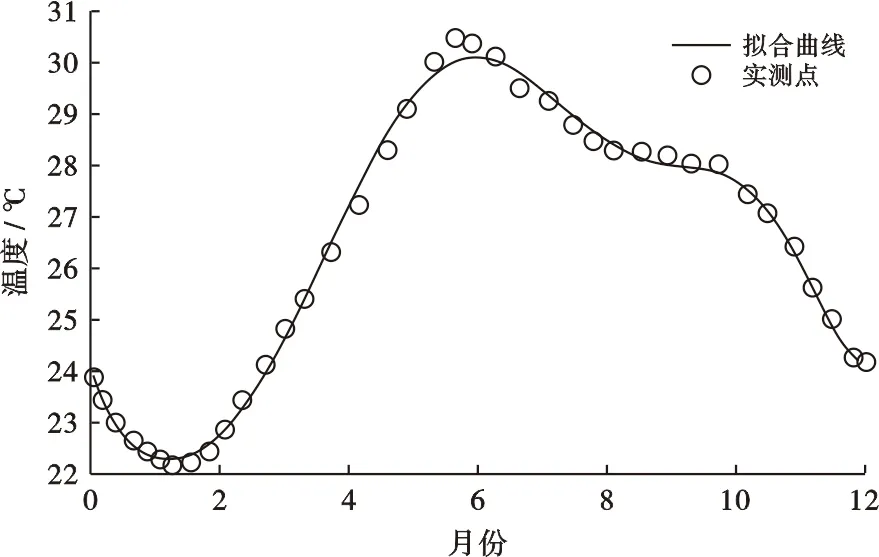
图3 莺歌海地区海水表层温度随季节变化曲线Fig.3 Surface temperature curve of Yinggehai with seasonal variation T表层=a1t8-a2t7+a3t6-a4t5+
a5t4-a6t3+a7t2-a8t+a9
(2)
式(2)中:t为月份,t=1~12,a1—a9为回归系数,a1=0.000 019 767 573、a2=0.000 880 403 84、a3=0.015 5、a4=0.135 7、a5=0.632、a6=1.66、a7=3.26、a8=3.84、a9=24.037 382。
2) 海水混合层和斜温层温度计算。
海水斜温层是混合层以下到深水层的温度变化层段。研究筛选后采用王宗山[13]对渤海、黄海、东海159个测量站的资料和所提出的海面的热量收支平衡计算公式,建立了海洋上均匀层厚度、温跃层强度和跃层下界深度的半经验半理论模型。
混合层深度
(3)
斜温层下界深度
(4)
斜温层强度
(5)

3) 浅海海水温度预测。
根据水温垂直分布曲线的形状,南海海域水温的垂直分布主要存在2种类型[6]:垂直均匀型和负梯度型。南海海域海水温度在春夏季会出现分层现象。东方13-1气田位于莺歌海海域,海图基准面水深约63 m。为获得混合层的温度随深度与短期内时间的变化,海洋温度场预测模型抽象为考虑垂向涡动的一维热传导问题[14],如式(6)~(8)。当用式(2)~(5)获取浅海海水温度剖面初值后,就可据其计算出准确的浅海海水温度剖面,该方程采用差分方法求解。
(6)
T(z,0)=q(z)
(7)
(8)
式(6)~(8)中:T浅海为浅海海水温度,K;k为垂直涡动热传导系数,W/m2;ρw为海水密度,kg/m3;Cw为海水热容,J/K;Iw为海面太阳辐射的透射分量,W;ν为光衰减系数,dB/km;Q(t)为海面热量平衡,W;H为水深,m。
4) 深水层温度计算。
由于深水层受太阳辐射、季风的影响较小,工程上可以认为深水层海洋温度梯度常年保持不变,可采用有代表性的区块实测温度梯度回归得到。本文采用1994年Levitus[15]在7°~12°N、111°~118°E、200~3 500 m深度内每隔一个经纬度的海水温度数据库,并结合南海各层水深的实测温度值拟合获得的南海海水垂向温度剖面计算公式,即
(9)
式(9)中:Tsea为深水层海水温度,K。
根据式(9)获得的隔水管外海水温度场随深度变化剖面如图4所示。图4中东方区块一口深水井的实测温度数据与预测数据对比,最大误差值为1.6 ℃,平均误差为1.15 ℃,大大降低了该段井筒传热引起的井底压力计算误差。
由此可以看出,通过利用海洋气象实测数据建立海洋表层温度预测方法和拟合获得深水层的海水垂向分布模型,组合一维垂向涡动传热模型和斜温层模型所获得的新的海水温度剖面预测方法,可以准确预测从海水表层至深水的温度剖面,从而有效降低隔水管外传热影响的压力计算误差。
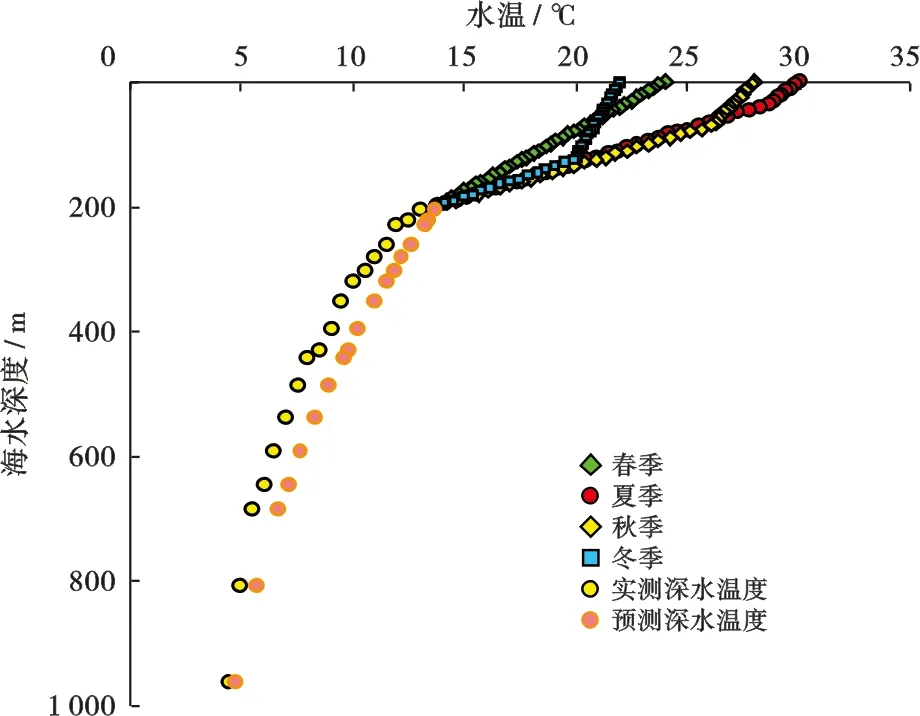
图4 东方区块某深水井海水温度剖面预测图Fig.4 Prediction chart of seawater temperature profile of a deepwater well in Dongfang Block
2.2.2隔水管外大气和海水段传热模型
在以往的计算中往往把隔水管外全部看成海水,而实际上隔水管上部还有一部分大气传热段,本文在研究中把它分离出来处理。隔水管外高于海平面的井段的传热,实际上和隔水管外海水段传热是类似的,只是其外部温度场为大气,因此以海水段传热模型建立为主,海平面以上的大气段仅需把海水总传热系数代换为由大气对流和辐射组成的总传热系数即可。
隔水管外壁向海水的传热存在垂向涡动换热、径向对流换热和径向热辐射等3种形式。由于存在洋流影响,隔水管外壁温度与海水温差较小,通过辐射热流密度定义容易得出隔水管壁向液体的热辐射可以忽略不计;另一方面,对于海洋的大尺度流动,海水垂向流速远远小于水平流速(存在显著上升流动的区域最大流速仅1×10-2cm/s),二者最大相差达3个量级[16],并考虑微元管段之间的管外温差相对小,故垂向涡动换热与径向对流换热相比小很多(一般相差2个量级),因此隔水管外壁向海水的传热模型考虑径向传热模型。总之,把海水段传热模型考虑为稳态模型,同时在隔水管外径向对流传热系数的计算中考虑洋流引起的垂向涡动传热系数的影响。井筒内传热单元控制体如图5所示。
根据热量平衡原理,在稳态传热中dz长度油管内流体到隔水管外壁的径向传递的热量可表示为
Q=2πrtoUto(Tf-Th)
(10)
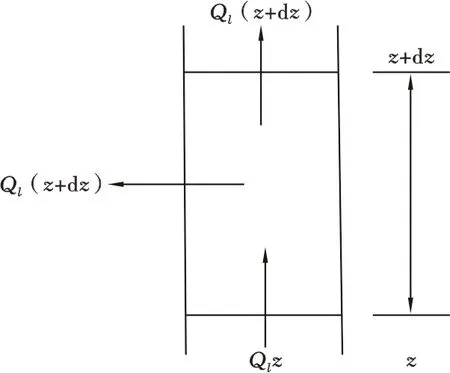
图5 气井传热管柱微元示意图Fig.5 Microelement schematic diagram of gas wellbore
式(10)中:Tf为油管内流体温度,K;Th为隔水管外壁温度,K;Uto为油管内流体至隔水管外壁的总传热系数,W/(m2·K);rto为油管外半径,m。
同理,dz长度隔水管外壁向海水的径向传热量为
Q=2πhtcr(Th-Tei)
(11)
式(11)中:htcr为隔水管外壁与大气或海水间的总换热系数,W/(m2·K);Tei为隔水管外大气或海水温度,K。
对于海水段,由于垂向涡动传热远小于洋流引起管外平面涡流传热,故可考虑htcr表示为
htcr=hcw+hrw
(12)
式(12)中:hcw为海水对流换热系数,W/(m2·K);hrw为海水辐射换热系数,W/(m2·K)。
(13)
其中,总传热系数U为
(14)
式(14)中:U为总传热系数,W/(m2·K)。
参考文献[17],由于海平面以上到油管挂的井身结构和海水段的井身结构相同,因此其传热方程和海水段的传热方程一致,油管中心到隔水管外壁的传热系数方程完全相同。
当式(14)用于隔水管外大气段传热计算时,隔水管外壁向外传热的外部温度应取大气温度,传热系数是大气的对流和辐射传热系数之和。
(15)
式(15)中:htair为考虑空气对流传热系数和辐射传热系数,W/(m2·K)。
选用Xiong等[18]基于计算流体动力学仿真提出的环空传热系数计算式,模拟过程采用真实大小的油管与环空尺寸,如式(16)。
(16)
式(16)中:hc为管外流体对流换热系数,W/(m2·K);rci为套管内半径,m;kc为静止流体的导热系数,W/(m·K);Re为雷诺数,无量纲;dto为油管外径,m。
由于空气和海水的流动性,因此在隔水管外部平面上存在风流和洋流会产生掠过圆管的涡流换热。对于井筒大气段,本文采用希尔波特(Hilpert)实验关系式来计算气体掠过隔水管(圆柱体)的平均表面传热系数的准则关系式[19],如式(17)。
结果显示,观察组的临床治疗效果要高于对照组,对照组100例患者中,有15例患者发生心血管事件,其发生概率为15%,其中4例心绞痛、6例心衰、3例心肌梗死、2例脑卒中;观察组的100例患者中,只有3例发生了心血管事件,其发生概率为3%,其中1例脑卒中、1例心衰、1例心绞痛。从以上结果可以看出,观察组出现心血管时间的概率要明显低于对照组,差异有统计学意义(P<0.05)[3]。
Nu=CRenPr1/3
(17)
式(17)中:Nu为努赛尔数,无量纲;Pr为普朗特数,无量纲;系数C与n的详细取值见表1。
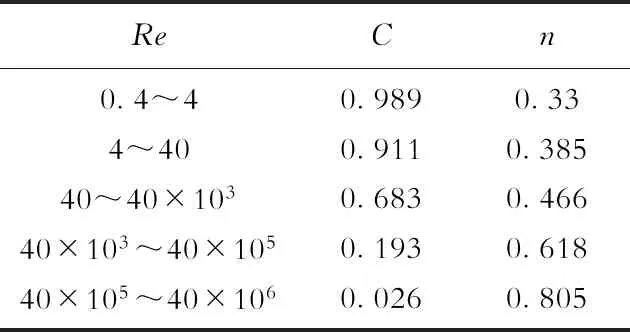
表1 式(17)中不同雷诺数下系数C与n的取值Table 1 Values of C and n at different Reynolds Numbers
对于海水段而言,不同流态下海水横掠隔水管的平均表面传热系数的准则关系式采用马永乾[6]提出的计算公式进行计算,如式(18)。
(18)
计算雷诺数Re所用到的海水流速采用袁耀初 等[20]基于南海东北部锚定测流站在450 m以浅水域和LongRanger ADCP超过70 d的测流资料所记录的海水流速数据拟合进行计算,如式(19)。
vsea=-2.277 48+19.261 7e-0.000 73H
(19)
式(19)中:vsea为海水流速,cm/s。
为了求解出沿井深的井筒内流体的温度变化剖面,因流出的热量是井筒油管内流体携带的热量的一部分,因此取图5所示的油管内微元,根据能量守恒定律,单元控制体内的流体能量守恒方程为
(20)
式(20)中:h为流体的焓,J/kg;vm为气体流速,m/s;wg为气体质量流量,kg/s。
由热力学基本理论可知,实际油管内流体的热量可用焓表示,因此流体温度和压力改变引起焓变为
dh=cpmdTf-αHcpmdp
(21)
式(21)中:cpm为流体的定压热容,J/(kg·K);αH为焦耳-汤姆逊系数,K/Pa。
将式(13)和式(21)代入式(20),并消去热流密度项,可得
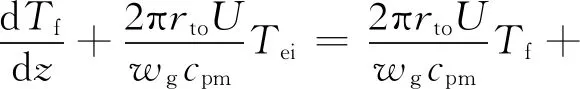
(22)
为便于分段计算,由式(22)通过解一元一次微分方程可得
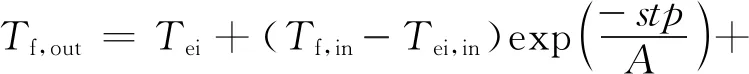
(23)
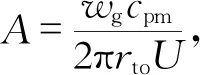
式(21)~(23)中的重力项gsinθ的符号取决于计算的坐标原点位置,当坐标原点为井口时,井底处记为井深H,重力项前面符号为正。当采用分段往井底计算时,已算出的节点为输入数据,采用式(24)进行计算。
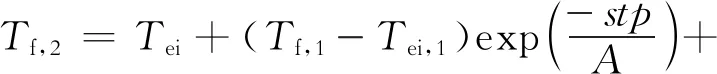
(24)
式(24)中:下标1、2表示相邻上下两节点。
2.3 泥线下井筒外部温度场和传热模型
在确定大气及海水段的外部温度场和传热模型后,需要建立泥线以下地层的传热模型。如果考虑泥线下具有恒温层的话,可引用地表恒温层深度的计算方法,但需要把风速等涉及大气变化的因素考虑为洋流等参数。实际上,泥线下的恒温层在莺歌海区块处较浅(不超过20 m),对计算结果影响较小,因此东方13-1气田高温高压气井井筒浅泥线以下的外部温度场可直接考虑为地温梯度,即
Tei=T泥线-gTH地层
(25)
式(25)中:Tei为地层温度,K;T泥线为泥线处的温度,K;H地层为以泥线为基准的深度,m。
同样,考虑为海水段一样的微元段处理和热量守恒原理来建立泥线以下的传热模型。油管到水泥环外缘的传热考虑为稳态传热,同式(10)。水泥环外缘向地层的传热考虑为不稳定径向传热,有
(26)
式(26)中:ke为地层传热系数,W/(m2·K);瞬态传热函数f(t)采用Remay函数[21]。
联立式(10)、(26)可得泥线以下地层油管内流体向地层的传热,其中总传热系数如式(27)。
(27)
地层传热段模型与大气、海水段传热模型的不同点主要为井筒流体与外部环境之间的总传热系数不同,因此可以直接参照海水段传热模型式(23)或式(24),此时井身水泥环外缘外部温度场用式(25)处理。
综上所述,本文将海上高温高压气井的外部温度场进行了更为详细的划分,并分别建立或筛选引用了最优的描述方法,获得了更为准确和精细的井筒外部温度场描述和传热描述,这是获得从井口到井底压力计算的高精度的基础之一。
3 温度-压力耦合计算
3.1 井筒水动力学方程
对流动气柱来讲,压力p一般采用式(28),静止气柱计算[22]采用式(29)。
(28)
(29)
考虑温度的影响及含水校正时,采用以下积分式[23]进行流压梯度的计算:
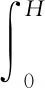
(30)
式(30)中:pwf为井底流压,ptf为井口流压,MPa;d为油管内径,m;Mg为气体相对分子质量;θ为井斜角,(°);Z为偏差因子;Fw为含水修正系数,其表达式如式(31)。
(31)
式(31)中:Qw为产水量,m3/d;Qg为产气量,m3/d。
设
(32)
(33)
借助于Cullender-Smith的计算方法[21],可以据式(30)、(33)得到每段的迭代关系式为
(34)
对于井筒静气柱计算方法而言,只需将式(30)或式(32)、(33)内的流体体积流量设为0即可。
3.2 井筒温度压力剖面计算步骤
1) 以井口为起点逐步向下计算,首先输入必要参数:井深、井口温度和压力、气体相对密度、外部温度场以及组分数据等,将整个井筒分成若干段,每段步长Δz。
2) 根据井口温度和压力以及上一时刻初始数据,假设每段上下节点温度压力值相等。
4) 利用段内平均温度、压力计算段内相关参数(偏差因子、密度、黏度等)。
5) 利用上一节点、段内参数和上一时刻初始值计算下一节点的温度值T1和压力值p1。
6) 返回步骤3),比较两次计算得到的下一节点温度压力值,若满足精度要求,则进入下一段温压计算,直至计算至井底。
4 实例计算分析
为验证本文所建模型的可靠性,采用东方13-1气田X井进行产能测试和压力恢复测试2个阶段的实例计算。该井为定向井,基本参数如表2所示,水深约63 m(相对海图水深基准面),补心海拔为40 m。

表2 东方13-1气田X井基本参数Table 2 Basic parameters of Well X in DF13-1 gas field
4.1 模型验证
东方13-1气田X井产能测试井底压力计算与实测数据如图6所示,可以看出考虑海水温度变化的一维预报方程耦合井筒温度、压力的计算模型精度较高。

图6 东方13-1气田X井产能测试井底压力计算值与实测值对比图Fig.6 Comparison between calculated and measured bottom-hole pressure of well productivity test of Well X in DF13-1 gas field
东方13-1气田X井压力恢复过程中井底压力计算与实测结果如图7所示,可以看出计算值与实测值基本吻合,本文计算模型精度高。根据本文井底压力计算得到的产能测试二项式曲线如图8所示,可以看出本文计算模型解决了产能测试二项式曲线斜率为负的问题。
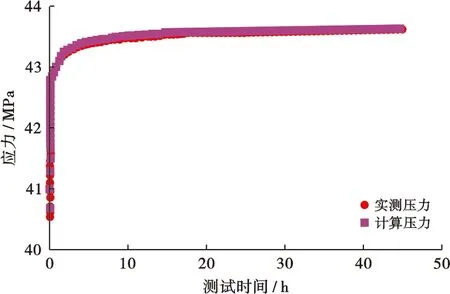
图7 东方13-1气田X井压力恢复过程计算压力与实测压力对比图Fig.7 Comparison between calculated and measured pressure in well pressure recovery process of Well X in DF13-1 gas field

图8 东方13-1气田X井产能测试二项式曲线Fig.8 Binomial curve of well productivity test of Well X in DF13-1 gas field
4.2 高温高压气井井底压力计算影响因素分析
为了更清晰表现细分外部温度场的效果,在参考已有的计算模型和方法基础上[23],结合式(20)、(21)及(26),分别对本文考虑所有因素、不考虑井口装置传热(从油管挂位置处进行计算)、不考虑井口装置传热与海水温度梯度(海平面以下环境温度场为线性分布)、不同因素叠加对压力剖面的影响、不考虑井口装置传热与大气和海水温度梯度(油管挂以下环境温度场为线性分布)、不考虑外部温度场细分和参数优化等5种条件下的井底压力计算误差进行了对比,结果见表3。表3中前4种情况采用DAK方法计算,第5种情况采用HY方法(主要考虑在中等压力、较高温度下,DAK的计算方法误差最小[24])。从表3可以看出,本文建立的计算模型精度最高、误差最小,不考虑井口装置传热对计算结果的影响最大。因此,对于深水气井本文方法中关于考虑海水温度层细分和洋流等对井底压力计算结果的影响将更加显著。

表3 考虑不同因素井底压力的计算误差Table 3 Calculating errors for different considerations
5 结论
1) 考虑井口装置和井筒隔水管外部温度场的影响,用实测数据回归获得的莺歌海地区海水温度随四季的变化曲线,结合考虑垂向涡动传热的一维海水预报模型可准确给出测试阶段的井筒外部温度场,温度预测相对误差绝对值最大值为1.6 ℃,平均误差为1.15 ℃,可大大降低隔水管段井筒传热引起的井底压力计算误差。
2) 在建立大气段、海水段、地层段传热模型的基础上,给出了计算敏感性较为显著的对流换热系数确定方法,采用传热-压力模型进行耦合计算可显著提高海上大斜度井的井底压力计算精度,实例验证流压计算误差在5‰以内,压力恢复计算平均相对误差为0.617‰。
3) 采用文中方法可有效解决东方13-1气田高温高压气井二项式产能测试曲线为负的异常问题,同时可克服关井恢复时温度场变化引起的井口压力下降的问题,利用关井井口压力计算的井底恢复压力能满足试井解释的精度需求。
——以嘉兴市为例

