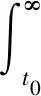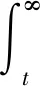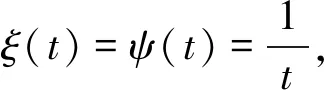时间尺度上二阶半线性时滞阻尼动力方程的振动性
李继猛,杨甲山
(1. 邵阳学院理学院, 湖南 邵阳 422004; 2. 梧州学院大数据与软件工程学院, 广西 梧州 543002)
本文研究时间尺度T上一类具阻尼项的二阶半线性时滞动力方程[1]
[a(t)|xΔ(t)|λ-1xΔ(t)]Δ+
b(t)|xΔ(t)|λ-1xΔ(t)+p(t)|
x(δ(t))|λ-1x(δ(t))=0,t∈T
(1)
的振动性,其中常数λ≥1为两个正奇数之商。 方程(1)的解及其振动性的定义, 可参见文[1-2]。 本文总假设:
(H1):T为任意时间尺度,且supT=∞。设t0∈T且t0>0,则[t0,∞)T=[t0,∞)∩T为时间尺度区间。
(H2): 时滞函数δ:T→T严格递增且可微,并且满足
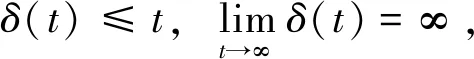
δ(T)=T。
(H3): 函数a,b,p∈Crd(T,(0,∞)),即它们均是正的实值rd-连续函数,且满足-b/a∈R+。
最近,关于时间尺度上动力方程的振动性的研究出现了很多成果[1-18]。如文[1-3,5]分别在条件
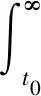
(C1)
和
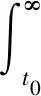
(C2)
下对方程(1)的振动性作了非常细致的研究,得到了一系列非常有价值的研究成果。主要结论如下:
定理A[1]假设条件(H1)~(H3)及(C1)成立,如果有一个正的可微函数φ:T→R使得
φ(s)Δs=∞
(C3)
则方程(1)在[t0,∞)T上是振动的。
定理B[1]假设条件(H1)~(H3)及(C2)成立, 并且
(C4)
如果有一个正的可微函数φ:T→R使得条件(C3)也成立,则在[t0,∞)T上方程(1)的每一个解x(t)或者振动或者收敛于0。

定理C[5]假设条件(H1)~(H3)及(C2)成立, 并且
(C5)

这是文[5]的定理4.3,由此条件(C5)就可得到方程(1)在条件(C2)成立时的其它种种类型的振动准则[3,5]。但值得注意的是,对于Euler(欧拉)方程
(t2x′(t))′+p0x(t)=0,t≥1
(E)

基于以上的研究和考虑,我们将在方程为非正则情形即在(C2)成立的条件下建立方程(1)振动的新准则, 推广、改进并完善现有文献中的一系列结果。
1 主要结果及证明
引理1(Keller连锁法则)[6]若f:R→R是连续可微的,g:T→R是Δ可导的, 则f∘g:T→R是Δ可导的, 且

由此引理可得, 当x(t)是Δ-可微的且最终为正或最终为负, 则有下式成立:

(2)
这也是Keller连锁法则的一个推论。
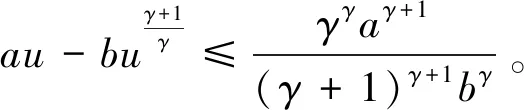
引理3[15]设γ≥1是2个正奇数之商,a和b是实数且ab≥0,则

(3)
其中函数θ(t),Φ(t)及Θ(t)的定义如下:
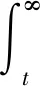
Φ(t)=p(t)-[ξ(t)a(t)]Δ-
则方程(1)在[t0,∞)T上是振动的。
证明不失一般性, 反设方程(1)在[t0,∞)T上有一个最终正解x(t)(若x(t)为最终负解时类似可证), 则存在t1∈[t0,∞)T, 使得x(t)>0及x(δ(t))>0(t∈[t1,∞)T)。于是,由方程(1)知,当t∈[t1,∞)T时
(a(t)|xΔ(t)|λ-1xΔ(t))Δ+
b(t)|xΔ(t)|λ-1xΔ(t)=
-p(t)xλ(δ(t))<0
(4)
情形(i):xΔ(t)>0(t∈[t1,+∞)T)。这种情形完全和文[1]中定理4.1的证明相同,得到一个与条件(C3)矛盾的结果。
情形(ii):xΔ(t)<0(t∈[t1,+∞)T)。令
(5)
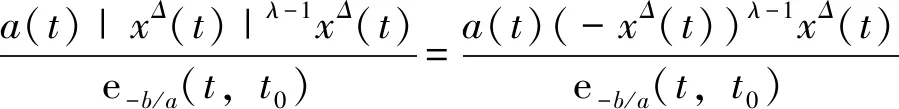
(6)

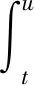
令u→∞,得
(7)
由于0 (8) 由式(2)及xΔ(t)<0, 容易推得 (9) 进一步, 由式(8)得 xλ(t)≥a(t)(-xΔ(t))λθλ(t) 注意到λ≥1为两个正奇数之商,故上式进一步可写成 (10) 令 t∈[t1,+∞)T (11) 则根据式(10),不难看出v(t)≥0(t∈[t1,+∞)T)。分别注意到式(4), 式(9)的第1个式子, 式(10)及xΔ(t)<0,由式(11), 就有 [ξ(t)a(t)]Δ-p(t)ψ(σ(t))- [ξ(t)a(t)]Δ-p(t)ψ(σ(t))+ (12) 将引理3中的不等式改成 (13) 注意到θΔ(t)=-[a-1(t)e-b/a(t,t0)]1/λ, 所以利用式(7),就有 现将上式及式(13)代入式(12), 并考虑到函数Φ(t)和Θ(t)的定义,就有 ψ(σ(t))a(t)ξ(λ+1)/λ(t)+ -ψ(σ(t))Φ(t)+Θ(t)v(t)- (14) 将引理2用于式(14),得 于是 -v(t)+v(t1)≤v(t1) 与条件(3)矛盾。定理证毕。 现记D0={(t,s):t>s≥t0,t,s∈T},D={(t,s):t≥s≥t0,t,s∈T}, 若函数H(t,s)∈Crd(D,R), 使得 (i)H(t,t)=0,t≥t0;H(t,s)>0,(t,s)∈D0; (ii)H(t,s)在D0上对s有连续且非正的偏导数, 即HΔs(t,s)∈Crd且HΔs(t,s)≤0, 则称函数H(t,s)属于集合Ω,记为H∈Ω。 (15) 其中常数t1≥t0, 函数θ(t),Φ(t)和Θ(t)的定义如定理1, 则方程(1)在[t0,∞)T上是振动的。 证明不失一般性, 反设方程(1)在[t0,∞)T上有一个最终正解x(t)(若x(t)为最终负解时类似可证), 则存在t1∈[t0,∞)T, 使得x(t)>0及x(δ(t))>0(t∈[t1,∞)T)。由定理1的证明知, 只有下列两种情形: (i)xΔ(t)>0,t∈[t1,∞)T;(ii)xΔ(t)<0,t∈[t1,∞)T 情形(i):xΔ(t)>0(t∈[t1,+∞)T)。这种情形完全和文[1]中定理4.1的证明相同,得到一个与条件(C3)矛盾的结果。 情形(ii):xΔ(t)<0(t∈[t1,+∞)T)。此时由定理1证明得式(14),将式(14)两边同乘以H(t,σ(s))后再积分,并利用时间尺度上的分部积分公式及引理2,可得 H(t,t1)v(t1)+ 整理,得 H(t,t1)v(t1)≤H(t,t0)v(t1) 即 这与条件(15)矛盾。定理证毕。 例1考虑二阶Euler微分方程(E): (t2x′(t))′+p0x(t)=0,t≥1 (E) 其中常数p0>0。 令a(t)=t2,b(t)≡0,p(t)=p0,δ(t)=t,λ=1,显然条件(H1)~(H3)及(C2)都满足。 注意到T=R,则 取φ(t)=1,则 即条件(C3)是满足的。 另一方面, 若取 则容易求得 于是当p0>1/4时,有 因此定理2的条件全部满足, 于是当p0>1/4时方程(E)振动。 注1我们也可以用定理1来判别方程(E)的振动性,所得结论是一样的,而且计算更简单。 例2考虑下列动力方程(二阶2-差分方程): t∈T=2z,t≥2 (16) 其中常数α>0。 显然,这相当于方程(1)中的 λ=1,t0=2。由于e-b/a(t,t0)=1,所以 令φ(t)=1,则有 因此条件(H1)~(H3)及(C2)和(C3)显然都满足。 另一方面,由于σ(t)=2t,且 于是由定理1知,当α>1/8时方程(16)是振动的。 注3显然,若用文[1-16]中的定理,则要么条件不满足,要么得到的结果不理想。因此,本文定理改进且丰富了现有文献中的结果。
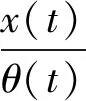


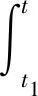
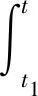
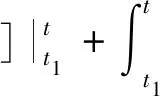
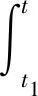
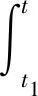
2 例子分析