基于载波相位差分的形变监测高精度定位算法

陈凯 孙希延 纪元法 王守华 陈紫强

摘 要：传统载波相位差分算法在形变监测领域适用性不足，实时动态定位（RTK）精度难以满足要求，而载波双差静态相对定位连续解算时形变跟踪性能较低等。针对这些问题，在对动静态算法深入研究的基础上，提出一种基于载波相位差分的动静态自适应融合算法。通过方差变化法实时判断定位结果是否收敛，自适应调节扩展卡尔曼滤波（EKF）状态先验估计过程。在收敛时刻增大位置参数的先验估计误差的协方差值，使EKF后验估计过程倾向于信赖测量值;未收敛时刻通过EKF迭代，使EKF后验估计过程倾向于信赖状态预测值。实验结果表明：相比传统RTK新算法精度有明显提高，水平达±2mm内，高程达到±4mm内;相比静态定位则缩减了观测周期，提高了微小形变跟踪性能。

关键词：形变监测;实时动态定位;静态定位;方差变化;定位精度

中图分类号：TN967.1

文献标志码：A

文章编号：1001-9081（2019）04-1234-06

Abstract： Traditional carrier phase difference algorithm is not suitable for deformation monitoring， the accuracy of Real-Time Kinematic （RTK） positioning cannot meet requirements and static relative positioning based on carrier double-differential phase has poor deformation tracking performance with continuous calculations. To solve these problems， based on the deep research of dynamic and static algorithms， a dynamic and static adaptive fusion algorithm based on carrier phase difference was proposed. The convergence of positioning results was judged by variance-change method in real time， then the state priori estimation process of Extended Kalman Filter （EKF） was adaptively adjusted. In the process， the covariance value of priori estimation error of position parameters was increased at the convergence time， so that the posteriori process of EKF tended to trust measured value. EKF iteration was used at the non-convergence time， so that the posteriori process of EKF tended to trust state predicted value. The experimental results show that compared with traditional RTK， the accuracy of the new algorithm is improved， with horizontal accuracy of ±2mm， and altitudinal accuracy of ±4mm. Compared with static positioning， the observation period is reduced， and the tracking performance of micro-deformation is improved.

Key words： deformation monitoring; Real-Time Kinematic （RTK） positioning; static positioning; variance-change; positioning accuracy

0 引言

全球衛星导航系统（Global Navigation Satellite System， GNSS）定位技术在形变监测领域具备自动化程度高、可同时测定三维位移及全天候等优势，已经广泛应用在如建筑物、桥梁、大坝和滑坡等监测领域。在实际工程应用中，当形变监测精度要求较高时（例如大坝、船闸监测的精度要求毫米级），或者在沉降监测领域，传统定位算法很难满足监测需要[1]。

目前，形变监测常用的GNSS定位算法有实时动态定位（Real-Time Kinematic positioning， RTK）[2]和载波双差静态相对定位（简称静态定位）[3]两种。传统RTK算法实时性和形变跟踪性能较高，但是受限于厘米级精度水平[2，4];静态定位精度可达毫米级，但实际工程应用中需周期性反复采集观测数据进行处理分析，且连续解算缺乏较好的形变跟踪能力，

文献[5]给出了相应的分析，并采用周期为10h的静态算法监测地面沉降。

针对传统算法的不足，张小红等[1]认为微小形变对双差观测值的影响远小于一周，在数据处理时可绕开周跳探测及整周模糊度确定问题;但是该方法依然会受到其他观测误差的影响，精度提高有限。文献[6]提出单双频接收机混合监测模式，通过利用双频接收机数据建立区域电离层模型，提高单频机的在沉降领域的监测精度;但是该方法因使用双频接收机导致布设成本高，且不适用于小区域监测，应用领域受限。文献[7]探讨了精密单点定位（Precise Point Positioning， PPP）算法在地面沉降、缓变性地质灾害监测中适用性问题，虽然采取精细误差修正模型改正，但精度依然难以满足毫米级要求。文献[8]构建的观测值域内的多路径误差模型实时改正观测值中的多路径误差后，三维位置精度可提高约30%。

针对传统算法在工程應用中的不足，本文提出了基于载波相位差分的动静态自适应融合算法。该算法采用方差变化法实时检测解算结果是否达到收敛状态，在非收敛时刻根据静态算法的扩展卡尔曼滤波（Extended Kalman Filter， EKF）策略不断迭代处理，提升其定位精度水平，而在收敛时刻根据实时动态算法的EKF策略自适应调节位置状态参数及其协方差值，改善其形变跟踪性能。

1 载波相位差分定位数学模型

监测站接收机r和基准站接收机b基于共视卫星i的载波相位观测值φ（i）r和φ（i）b分别为：

2 方差变化法

检测出静态定位结果的收敛时刻能有效提高新算法的形变跟踪性能。静态定位结果时间序列具有由非平稳逐渐收敛到平稳的特点，确定收敛时间，只需要判断该时间序列中非平稳部分和平稳部分的过渡点。若判断出时间序列收敛点，根据该收敛点的观测历元就可以得到快速静态定位收敛时间[10]。

非平稳序列的方差值较大，波动也较大;而平稳序列的方差值接近零，波动比较小。因此，本文采用方差变化法，从方差的角度判断出序列收敛点。

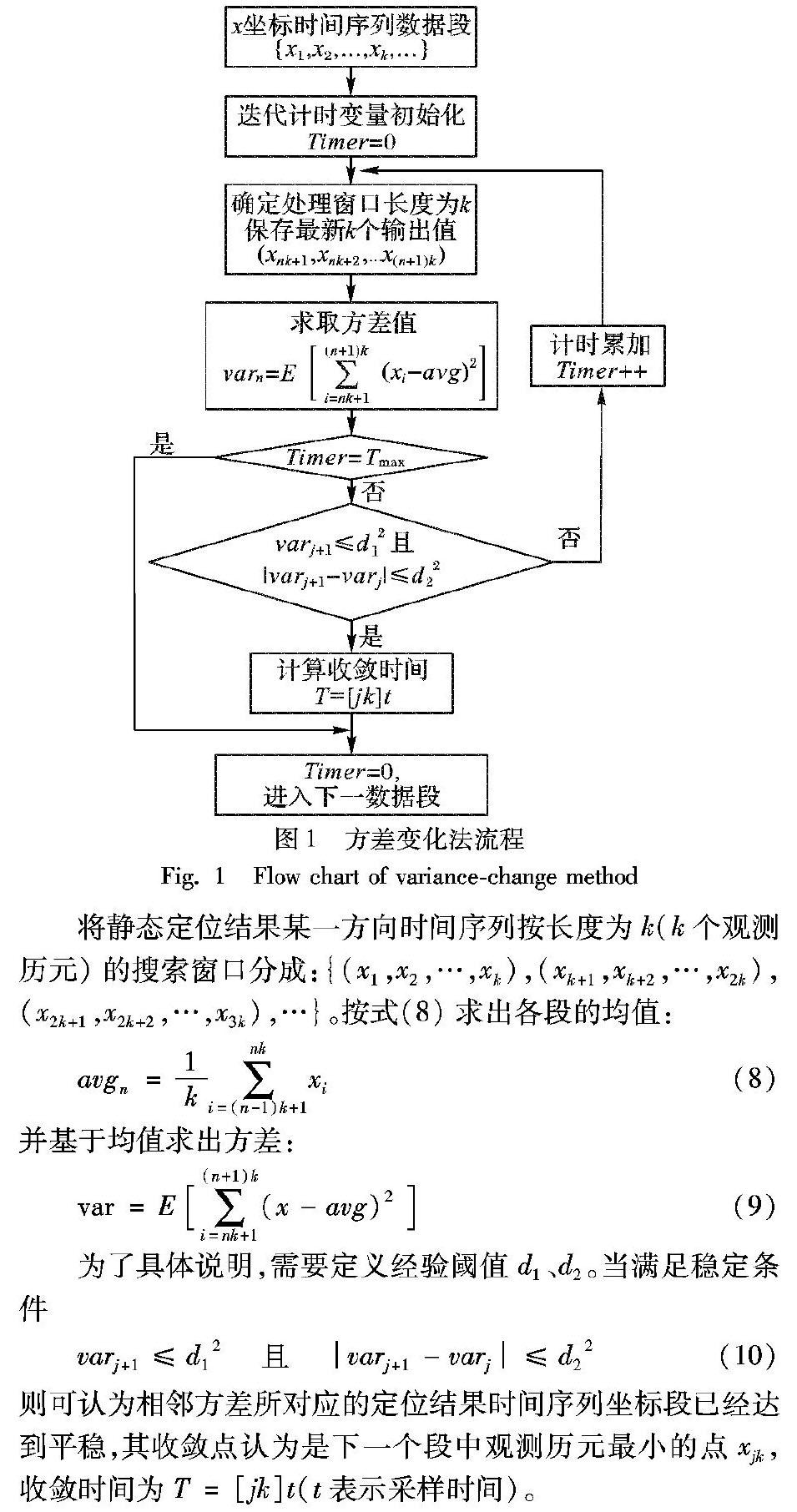
方差变化法的流程如图1所示。

为了具体说明，需要定义经验阈值d1、d2。当满足稳定条件则可认为相邻方差所对应的定位结果时间序列坐标段已经达到平稳，其收敛点认为是下一个段中观测历元最小的点xjk，收敛时间为T=[jk]t（t表示采样时间）。

经实验，当监测区域观测环境较好时，静态定位能较快达到收敛要求，且发散概率很小。但是恶劣环境下，受到多路径和周跳等观测误差影响，会在某时段造成静态定位收敛时间较长，甚至出现发散的情况，从而导致方差变化法在经验阈值下不能得到收敛时间。考虑到现场环境且在满足GNSS技术监测要求条件下，方差变化法必须满足以下条件：

1）定义数据段迭代时间限值Tmax，取较好观测环境下数据段迭代收敛时间的最大值。如果迭代时间超过该值还未收敛，则停止迭代并进入下一数据段处理。

2）阈值d1、d2根据监测环境选取经验值，但要满足在Tmax下有85%以上的数据段可收敛。

3 动静态自适应融合载波相位差分算法

3.1 载波相位差分定位算法

在定位算法中，采用最小二乘法（Least Squares， LS）的处理结果通常会受到误差与噪声的影响，显得既粗糙又杂乱，而EKF能有效降低、分离信号中所含的噪声量，得到平滑、准确的定位结果[11]。

其中：D为整周模糊度单差转双差矩阵;X为状态向量，包括监测站位置三维坐标、三维速度、三维加速度参数和单差整周模糊度参数，但是在形变精密监测领域中，载体不会发生高动态运动，因此状态矩阵中通常会舍弃三维速度和三维加速度参数;xr、 yr、zr为监测站三维位置参数;Nirb是基于共视卫星i的站间单差整周模糊度参数，为了避免参考星的变换对双差整周模糊度固定的影响，在对双差整周模糊度搜索处理前才将Nirb转换为双差形式。

在载波相位差分定位中，当前位置参数利用前一步的预测值确定，如果不发生周跳，认为双差整周模糊度参数是连续的[9]，因此给出状态方程及预测值的方差阵：

其中：X^k-1表示k-1历元的状态后验估计向量;A表示状态转移矩阵;X-k表示k历元的状态先验估计向量（状态预测向量）;P^k-1表示k-1历元的后验估计误差协方差矩阵;P-k表示先验估计误差的协方差矩阵;Q表示过程噪声向量的协方差矩阵。

其中：R表示观测误差协方差矩阵;yk表示观测值向量。

实现载波差分定位的核心问题之一是解算整周模糊度的整数解[2]。双差载波相位方程组（5）中包含监测站位置和双差整周模糊度未知参量，对于实时动态和静态定位系统，希望尽可能地快速、简单而又可靠地完成整周模糊度的求解。

是常用的双差整周模糊快速求解算法，可在少数历元下确定双差整周模糊度的最优值。由式（24）可得到三维坐标固定解：

其中：为三维坐标浮点解;为三维坐标固定解;为整周模糊度固定解向量;为整周模糊度浮点解向量;Q是坐标参数和整周模糊度参数的协方差阵;Q-1是整周模糊度协方差的逆矩阵。

3.2 RTK算法中的EKF先验估计过程

在RTK定位算法中，如果不发生周跳，认为双差整周模糊度参数是连续的，在状态矩阵先验估计过程中不需要对其进行处理。又因为状态矩阵中不包含三维速度和三维加速度参数，根据式（18），在EKF的状态先验估计过程中，基于当前历元k的状态转移矩阵可设计为：

其中：I为单位矩阵;n为两站间共视的卫星颗数。为了保证RTK算法的实时动态性，对基于式（18）的EKF状态矩阵先验估计过程进行了调整。分为两种情况：

可以看出，在RTK算法的EKF先验估计过程中，在每一历元均基于当前历元的单点坐标更新状态矩阵的位置参数部分，并将相应的先验估计误差的方差数值设置为900。增大先验估计误差的方差，说明当前预测状态矩阵中三维位置相对不可靠或者测量值相对准确，会使式（20）得到的增益值倾向于信任测量值yk而减少对预测值的依赖[11]。该过程能有效保证算法的实时动态性，在实际监测中，可及时反映出监测体的形变。

3.3 静态定位中的EKF先验估计过程

静态定位中采用了和RTK同样的状态转移矩阵A，为了提高定位的精度，在EKF先验估计过程中，采用了不同于RTK的处理方式。静态定位过程中先验估计状态矩阵及其协方差矩阵更新为：

静态定位不同于动态定位，它在非首历元没有对状态矩阵及其协方差矩阵进行更新和初始化，而是通过不断迭代收敛过程，达到高精度。随着不断迭代，其先验估计误差的协方差会逐渐变小，说明当前状态先验矩阵中三维位置相对可靠或者测量值相对不准确，会使式（20）得到的增益值倾向于信任预测值而减少对测量值的依赖，导致定位结果不断趋于稳定，精度不断提高。但是，该算法收敛到稳定状态时，由于先验方差值较小，将无法及时反映出监测体形变[14]。

3.4 動静态自适应融合算法

实际工程应用中，定位精度和形变跟踪能力是算法性能的两个重要指标。新算法在基于动静态算法研究的基础上，通过方差变化法对收敛时间的判断，自适应融合动静态算法EKF的状态先验估计过程，使其在满足精度的同时提高形变跟踪性能。动静态自适应融合算法的具体步骤如下：第1步 建立载波相位双差方程组，如式（5）。针对方程组的非线性，进行线性化得到式（14）。

第2步 对式（14）采用EKF的先验估计过程进行处理，该过程分为3种情况：1）若当前历元为首历元，则先验估计状态矩阵及其协方差矩阵根据式（27）～（28）进行更新。

2）若当前历元为非首历元，且基于第5步，根据方差变化法判断当前历元未满足收敛要求，则将先验估计状态矩阵及其协方差矩阵按照式（31）～（32）进行更新。

3）若当前历元为非首历元，且基于第5步，根据方差变化法判断当前历元满足收敛要求，则将先验估计状态矩阵及其协方差矩阵按照式（29）～（30）进行更新。

第3步 对式（14）进行EKF的状态更新过程（状态矩阵的后验估计过程），如式（20）～（22）。

第4步 采用LAMBDA/MLAMBDA搜索整周模糊度，通过式（24）得到当前历元的三维位置固定解。

第5步 保存解算结果，对解算结果形成的时间序列通过方差变化法进行收敛性判断。若当前历元判断收敛，则输出收敛结果;否则，进入下一历元解算。

4 算例与分析

为了验证动静态自适应融合算法的有效性并比较RTK、静态定位和本文算法在精密形变监测领域中的实际效果，做了如下3个实验：1）检验方差变化法的有效性;2）基于静态数据处理实验，比较动静自适应融合算法和传统算法的精度;3）模拟微小形变实验，检验动静自适应融合算法的形变跟踪性能。

4.1 方差变化法有效性检验

实验1的是用来检验方差变化法的有效性，先构建原始观测时间序列如下：

式（33）是一个Matlab函数，生成满足C～N（0，0.005），时间序列长度为1000的随机数，并采用卡尔曼滤波（Kalman Filter， KF）算法对该序列进行滤波处理，处理结果作为方差变化法输入的时间序列，最后通过方差变化法对该时间序列进行收敛性分析。实验中，方差变化法的搜索窗口、收敛阈值和迭代时间限值分别设置为：k=10，d1=5×10-4、d2=1×10-4，Tmax=400s。如图2所示，实验分别得到随机时间序列曲线（原始观测数据曲线）、KF滤波结果曲线、序列段方差曲线和方差变化曲线。

根据图2，在历元达到200s后，方差曲线和方差变化曲线趋于平稳，其中，方差曲线还呈收敛趋势。通过数据分析，在满足序列段方差值小于d12，且方差变化值小于d22时，序列收敛时间在210s处。基于KF滤波曲线可以看出，达到收敛时间后，滤波曲线波动明显变小，已经达到平稳状态。

基于式（39），随机生成8组时间序列，分别通过方差变化法处理后得到收敛时间，结果如表1所示。

根据表1，不同随机时间序列得到的收敛时间之间差异很大，说明不同序列收敛快慢可能不一致。在序列收敛较快时能及时检测出收敛时间，可有效提高新算法的形变跟踪能力。

4.2 解算精度分析

实验2在某大学图书馆楼顶进行，基准站和监测站均采用ublox M8T型兼容美国全球卫星定位系统（Global Positioning System， GPS）和中国北斗卫星系统（BeiDou System， BDS）的双模单频接收机采集数据。两站均保持固定不动，距离约为64m，且已知的精确的坐标采用精密星历并基于GAMIT软件处理得到。

数据采集时间为2018年6月20日至21日，观测86400个历元，数据采样间隔为30s，卫星高度截止角为15°，接收到的BDS卫星有9～11颗，GPS卫星有6～10颗，如图3所示。

实时数据分别采用RTK算法、静态算法和动静态自适应融合算法处理。如图4～6，分别为基于不同算法处理后的坐标与已知精确坐标的差值三维曲线图。其中，动静态自适应融合算法中方差变化法的搜索窗口长度、收敛阈值和最长迭代时间分别取经验值：k=60s，d1=d2=0.001m，Tmax=3600s，实验过程未出现数据段迭代时间超过Tmax值的情况。

通过将处理得到的定位结果和已知的移动站精确坐标进行比较，可求得各个算法定位结果的外符合精度。表2是基于不同算法下定位结果和已知精确坐标绝对差值的2Sigma统计。

根据图4～6和表2中的结果可以看出，RTK、静态定位（24h）和动静态自适应融合算法的南北向外符合精度MN分别为：±4.2mm、±0.14mm、±1.5mm，东西向外符合精度ME分别为：±4.6mm、±0.26mm、±1.2mm，高程MU外符合精度分别为：±10.2mm、±1.4mm、±3.6mm，其中静态定位外符合精度与迭代时间成正比。动静态自适应融合算法水平外符合精度达到±2mm内，高程外符合精度达到±4mm内，较RTK算法有了显著提高。

4.3 形变跟踪性能分析

为模拟实际监测环境，实验3将监测站天线放置到观测环境较差的教学楼顶，基准站位置不变，两站之间距离约521m。其中，监测天线北侧受到移动公司基站机房遮挡，南侧受到树木影响。实验中将监测站天线放置到模拟形变的可移动平台上，该平台可在相互垂直的三个方向移动，测微器可精确测定移动量，精确至0.01mm，故可视为已知值，未移动前的精确坐标可基于实验2通过GAMIT软件得到。

实验在2018年6月25日至26日进行。开始时间为25日10时，从实验开始至26日10时保持监测天线固定不动，以后每隔1h在南北向移动0.5mm，在高程方向移动1mm，共移动10h。观测172800个历元，数据采样间隔为30s，卫星高度截止角为25°，以减小低仰角卫星的影响，接收到的BDS卫星有7～10颗，GPS卫星有5～8颗。

实时数据分别由RTK、静态定位、动静态自适应融合算法处理，其中动静态自适应融合算法中方差变化法的搜索窗口长度k、收敛限值和迭代时间限值分别设置为：k=60s，d1=d2=0.0025m，Tmax=3600s，相比实验2，由于为保证恶劣环境下收敛，增大收敛阈值，处理过程中未出现收敛时间超出Tmax值的情况。

如图7～8所示，为不同算法处理结果偏移量和实际偏移量在南北和高程方向的比较。根据表3和图7～8，RTK、静态定位（24～48h）和动静态自适应融合算法的南北向外符合精度MN分别为：±5.1mm、-3.3mm、±1.8mm，高程外符合精度MU分别为：±18.3mm、-7.8mm、±3.9mm。其中，RTK算法外符合精度大于微小形变量，处理结果无法直观反映出微小形变;监测天线移动后，静态定位算法外符合精度明显下降，说明其连续解算时形变跟踪性能较差;动静态自适应融合算法不管在水平方向还是高程方向形变跟踪性能均优于其他两种算法。

5 结语

本文介绍了RTK和静态算法基于EKF滤波过程的不同对精度和形变跟踪性能的影响，提出了一种适用于精密形变监测领域的动静态自适应融合新算法。从实验结果可看出，与RTK算法相比，新算法精度显著提高，符合精密形变领域的监测精度要求;相比静态定位和RTK算法，其微小形变跟踪性能较好。这表明新算法融合了高精度和微小形变跟踪性能的优势，有利于GNSS技术在精密形变监测领域的应用。

参考文献（References）

[1] 张小红， 李征航， 徐绍铨.高精度GPS形变监测的新方法及模型研究[J]. 武汉大学学报（信息科学版）， 2001， 26（5）： 451-454. （ZHANG X H， LI Z H， XU S Q. A new method for high accuracy deformation monitor with GPS[J]. Geomatics and Information Science of Wuhan University， 2001， 26（5）： 451-454.）

[2] 王世进， 秘金钟， 李得海， 等.GPS/BDS的RTK定位算法研究[J]. 武汉大学学报（信息科學版）， 2014， 39（5）： 621-625. （WANG S J， BEI J Z， LI D H， et al. Real-time kinematic positioning algorithm of GPS/BDS[J]. Geomatics and Information Science of Wuhan University， 2014， 39（5）： 621-625.）

[3] 袁本银， 鲍志雄， 潘国富.GPS/BD静态相对定位解算研究与实现[J]. 测绘， 2012， 35（6）： 247-250. （YUAN B Y， BAO Z X， PAN G F. Research and realization of GPS/BD static relative positioning solution[J]. Surveying Mapping， 2012， 35（6）： 247-250.）

[4] HE H B， LI J L， YANG Y X， et al. Performance assessment of single- and dual-frequency BeiDou/GPS single-epoch kinematic positioning[J]. GPS Solutions， 2014， 18（3）： 393-403.

[5] 王利， 张勤， 范丽红， 等. 北斗/GPS融合静态相对定位用于高精度地面沉降监测的试验与结果分析[J]. 工程地质学报， 2015， 23（1）： 119-125. （WANG L， ZHANG Q， FAN L H， et al. Experiment and results of high precision land subsidence monitoring using fused BDS/GPS data and static relative positioning[J]. Journal of Engineering Geology， 2015， 23（1）： 119-125.）

[6] 张超， 戴吾蛟， 石强， 等. 电离层延迟对单频GPS点的影响及改正方法研究[J]. 武汉大学学报（信息科学版）， 2018， 43（3）： 471-477. （ZHANG C， DAI W J， SHI Q， et， al. Influence of ionosphere delay on single frequency GPS point and its correction method[J]. Geomatics and Information Science of Wuhan University， 2018， 43（3）： 471-477.）

[7] 王利. 地质灾害高精度GPS监测关键技术研究[J]. 测绘学报， 2015， 44（7）： 826-826. （WANG L. A study on key technology of high precision GPS monitoring for geological hazard[J]. Acta Geodaetica et Cartographica Sinica， 2015， 44（7）： 826-826.）

[8] 易清根， 刘心龙， 刘万科. 基于EMD和小波的GPS/BDS变形监测中的多路径误差削弱方法[J]. 大地测量与地球动力学， 2017， 37（5）： 462-466. （YI Q G， LIU X L， LIU W K. Multipath mitigation method by combined EMD and wavelet in GPS/BDS deformation monitoring[J]. Journal of Geodesy and Geodynamics， 2017， 37（5）： 462-466.）

[9] 王趁香， 葛茂荣， 祝会忠， 等.BDS/GPS组合静态相对定位算法探讨[J]. 导航定位学报， 2017， 5（2）： 93-97， 102. （WANG C X， GE M R， ZHU H Z， et al. Discussion on static relation positioning algorithm of combined BDS/GPS[J]. Journal of Navigation and Positioning， 2017， 5（2）： 93-97， 102.）

[10] 葛春蕾.时间序列的变点估计的相合性和收敛速度[D]. 合肥： 合肥工业大学， 2007： 25-29. （GE C L. The consistency and convergence rate of the change-point estimation of rime series[D]. Hefei： Heifei Institute of Technology， 2007： 25-29.）

[11] 謝钢.GPS原理与接收机设计[M]. 北京： 电子工业出版社， 2009： 126-131. （XIE G. Principles of GPS and Receiver Design[M]. Beijing： Publishing House of Electronic Industry， 2009： 126-131.）

[12] TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment： a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy，1995，70（2）：65-82.

[13] CHANG X W， YANG X， ZHOU T. MLAMBDA： a modified LAMBDA method for integer least-squares estimation[J]. Journal of Geodesy， 2005， 79（9）： 552-565.

[14] 陈鹏.基于单历元解算的实时变形监测技术的研究与算法实现[D].沈阳：东北大学，2014：1-24.（CHEN P. Research and algorithm development of real-time deformation monitoring technology based on GPS single epoch calculation. Shenyang： Northeastern University， 2014： 1-24.