基于TOPSIS-灰色关联方法的水资源配置评价模型研究

孙国营，陕振沛，孙新杰，张文林

(六盘水师范学院 数学与信息工程学院，贵州 六盘水 553004)

水资源是人们不可或缺的资源，人们每一天都离不开水，水对人们日常生活、工业生产以及经济发展都有着举足轻重的作用。虽然水是可再生资源，但是随着人口的增加、环境的破坏、用水量的增加等等原因，水资源在某些国家和地区已经变成了稀缺资源。为了合理利用水资源，必须选取最优的水资源配置方案。关于水资源配置方法的评价已经有很多的研究，如陈晓楠[1]的基于粒子群的大系统优化模型在灌区水资源优化配置中的应用；郭宗楼[2]的灌溉水资源最优分配的DP-DP法；李志新[3]的基于模式识别神经网络的水资源配置评价模型研究；宏瑾靓[4]的改进物元可拓法在水资源优化配置方案评估中的应用；桑学锋[5]的面向总量闭合的水资源配置模型与应用；韩雁贾[6]的柴达木盆地水资源供需配置规划；孙博文[7]的不确定条件下农用水资源配置与多元利用研究；刘彬沙[8]的基于区域用水户用水安全的水资源配置方法研究。关于水资源配置评价的文献远不止本文所列出的这些。从前期的研究成果来看，对水资源配置评价的研究方法主要有层次分析法、熵权法、TOPSIS算法、灰色关联算法等等，这些算法可以在一定程度上实现水资源配置评价研究，但是也有一定的局限，主要体现在以下方面：一是在计算权重时对一些特殊数据难以处理；二是评价方法比较单一，评价结果不甚理想；三是即使有一些评价方法使用了多个算法的组合，但是组合方式过于简单，缺少创新性。本文在总结现有研究方法的基础上，首先通过改进熵值法确定权重，然后分别对TOPSIS方法和灰色关联决策方法进行改进，共同用于求解不同水资源配置方案的相对贴近度，按相对贴近度的数值大小进行排序，选取最优配置方案。最后将该模型应用到某市4个水资源配置方案的评价中，得到的评价结果和实际情况基本相同。

1 改进的TOPSIS-灰色关联模型

基于熵值的改进TOPSIS-灰色关联方法的基本原理为：首先对原始矩阵进行标准化处理，得到标准化决策矩阵；然后通过改进熵值法求解权重；将TOPSIS方法进行改进后得到新的决策矩阵中各方案到新的负理想解的欧式距离以及到新的正理想解的欧式距离，将灰色关联算法进行改进后得到各方案与新的负理想解以及新的正理想解的灰色关联度，综合上述四个值得到各个方案的相对贴近度。

1.1 基本假设及指标预处理

假设有m个方案，每个方案包含n个指标，mij(i=1,2,…,m，j=1,2,…,n)为第i个方案第j指标下的原始数据，则初始矩阵为：

(1)

因初始矩阵中不同指标的量纲和数量级可能不同，为消除它们带来的影响，必须对原始数据进行标准化处理，使之无量纲化和归一化。

对越大越好的效益型指标，标准化处理的公式为[9]：

(2)

对越小越好的成本型指标，标准化处理的公式为[9]：

(3)

1.2 改进熵值法确定权重

熵是系统无序程度的一个度量，指标提供的信息量和熵值呈反比，熵值越大，指标提供的信息量越小，权重就越小。使用传统的熵值法求解权重有一定的弊端，例如：如果mij=0，在计算mijlnmij时不能保证对数函数内的值大于零，会出现计算公式没有意义的情况。为了克服这些弊端，本文对熵值法进行改进，具体步骤如下：

(1)第j个指标的熵值Nj的计算公式如下[10]：

(5)

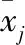
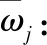
(6)

(7)

(3)得到指标权重向量W：

(8)

1.3 利用改进TOPSIS-灰色关联算法确定理想解

TOPSIS方法可以对有多个属性的指标进行综合评价，判断其优劣。灰色关联算法可以根据不同指标的多个属性与最差样本和最佳样本之间的关联度判断样本优劣。两种算法都可以实现判断多属性指标优劣的功能，将两种算法结合起来实现水资源配置方案的评价，求解结果更加合理，和实际情况更贴切。

将通过改进熵值法计算得到的权重向量W与标准化决策矩阵相乘，得到加权标准化矩阵Z：

(9)

式中：zij为加权标准化矩阵Z中第i行第j列的数值。

确定各个方案的初始负理想解Z0和初始正理想解Z1：

(10)

(11)

计算zij到初始负理想解Z0以及初始正理想解Z1关于第j个指标的灰色关联系数pi(j)和hi(j)分别为：

(12)

(13)

式中：ρ的取值范围在0～1之间，通常取ρ=0.5样本。

通过式(12)可以求出各方案与初始负理想解Z0的灰色关联系数矩阵P，通过式(13)可以求出各方案与初始正理想解Z1的灰色关联系数矩阵H为：

(14)

(15)

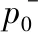
(16)

(17)

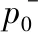
(18)

(19)

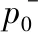
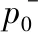
(20)

(21)

(22)

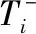
(23)

式中：α和β均属于[0,1]且α+β=1，通常情况下，取α=β=0.5。

将求得的相对贴近度Ci按数值进行排序，Ci越大，表明方案越好，Ci越小，表明方案越差。

2 实例应用

下面以文献[11]中某市各水资源配置方案评价指标值为例，选取资源效益、社会效益、生态效益和经济效益4个方面进行评价，建立包含人均用水量、渠系水利用系数、水资源开发利用率等15个比较典型的指标进行研究，建立如表1所示的某市各水资源配置方案评价指标表。

通过公式(2)、(3)对该市4个方案的原始数据进行标准化处理，标准化后的数据如表2所示。

表1 某市各水资源配置方案评价指标表

表2 某市各水资源配置方案标准化处理后的数据

利用公式(4)～(7)改进熵值法得到各评价指标的权重：

W=(0.08,0.03,0.05,0.03,0.03,0.06,0.04,0.08,0.08,

0.04,0.09,0.08,0.04,0.07,0.20)T

根据式(9)求得加权标准化矩阵Z：

由公式(10)、(11)分别求出不同方案各个评价指标的初始负理想解Z0和初始正理想解Z1：

Z0=(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)

Z1=(0.08,0.03,0.05,0.03,0.03,0.06,0.04,0.08,

0.08,0.04,0.09,0.08,0.04,0.07,0.20)

根据公式(12)、(13)确定灰色关联系数矩阵P和H：

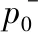
0.56,0.56,0.71,0.53,0.56,0.71,0.59,0.33)

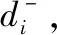
由式(23)计算每个方案的相对贴近度Ci，并由大到小进行排序，最终结果如表4所示。

从表4可以看出4个方案按优劣排序为：方案4>方案1>方案2>方案3。这4个方案中方案4最优，其次是方案1，方案3是最差的，因此应该选择方案4来实施。本文结果与文献[11]的实际情况相符，说明此方法是有效的，能够运用到求解水资源配置最优方案的实际应用中。

3 结 语

本文旨在为求解水资源配置最优方案提供一种的新的评价方法，所用方法的优越性主要体现在以下3个方面：

(1)针对传统熵值法存在的缺陷，将传统熵值法进行改进后求解权重，避免了计算权重的过程中经常性的出现的ln 0的情况，扩展了熵值法的应用范围，并使求解的结果更加合理。

(2)将TOPSIS方法进行改进后得到新的决策矩阵中各方案到新的负理想解的欧式距离以及到新的正理想解的欧式距离，将灰色关联算法进行改进后得到各方案与新的负理想解以及新的正理想解的灰色关联度，综合上述4个值得到各个方案的相对贴近度。改进后的算法更加优越，计算结果更加合理，和实际情况更加相符。

(3)本方法可扩展性强，不但可以应用到求解水资源配置最优方案中，还可以应用到节水灌溉效益最优、最佳物流供应商选择等多个领域的实际问题求解中。