农产品期货期权定价的有效性研究——以我国豆粕期货期权为例

马庆华,郭 倩

(广东外语外贸大学 金融学院,广州 510006)

期权定价主要包括三种方法：B-S模型，二叉树模型以及蒙特卡洛模拟。Barone-Adesi和Whaley提出的美式期权近似解模型(BAW模型)将美式期权的解分为两部分，一部分是同等欧式期权的解，另一部分是由于合约提前实施条款而需要增付的权利金，并认为美式期权价格和欧式期权价格都满足Black-schole方程，所以提前实施的权利金也符合B-S方程[1]；Cox Ross和Rubinstein的二叉树模型既适合于欧式期权又适合于美式期权，且方法简单易懂，之后被投资者们广泛运用，其缺点就是当步长增加时，计算耗时增大[2]；Longstaff和Schwartz提出的最小二乘蒙特卡洛模拟(LSM)被广泛用来当作美式期权定价的标准[3]。

关于期权定价的对比分析大都是基于两种模型或者是基于外国期权产品的实证研究，没有结合三种模型且基于本国期权产品的实证研究。刁博珏等用Microsoft的股票期权作为样本，使用Matlab和Excel并运用二叉树模型以及蒙特卡洛模拟法对股票期权进行了理论定价研究，并将两种方法的定价结果同实际的期权价格进行了比较[4]；方艳等分别运用B-S-M模型和蒙特卡洛模拟方法对上证50ETF的定价进行了实证研究，认为两种方法都能比较精准地对上证50ETF进行定价，还用平均绝对误差(MAE)、均方比例误差(MSPE)、平均绝对比例误差(MAPE)来检验模型定价的稳健性[5]。

对农产品期权定价的研究，或是根据外国期权市场的数据，或是通过对我国的订单农业进行摸索而进行模拟定价。Foster 和Whiteman加入数值贝叶斯技术建立了标的资产价格的预测密度，以芝加哥期货交易所交易的大豆期货期权为例，探讨B-S模型、Stutzer模型以及经改进后的贝叶斯技术模型哪一种模型更接近实际期权价格[6]；黄亚林根据芝加哥期货交易所的玉米、大豆和小麦期权的数据，从农产品价格风险规避的视角对其期权定价进行研究[7]；田贵良等提出用虚拟水期权来规避粮食安全和农业生产的风险，构建了一个适合虚拟水产品的“扩散-跳跃”模型,并用郑商所的小麦作为实证得出小麦虚拟水期权的价格[8]。

2016年12月16日，证监会批准郑商所和大商所分别开展白糖和豆粕期货期权交易，这意味着国内首个场内农产品期权落地。在2017年3月31日豆粕期货期权挂牌首日共成交了46066手，持仓量为32056手。总体而言，市场交易比较理性，成交平稳。从其期权合约设计来看，它反映了服务实体的特征，严格控制了市场风险。而豆粕期货期权自从上市以后，大商所不断放宽其限仓标准，从刚开始的300手到2017年9月的2000手，再到2018年5月的1万手，接着2019年2月放宽到3万手。这说明了我国豆粕期权的快速发展和投资者的需求日渐增加，这也更有利于投资者们充分利用豆粕期权的丰富的交易策略，更好地满足他们自身的风险管理需求。豆粕期货期权是由大连商品交易所制定的。

鉴于我国农产品期权市场起步较晚，关于农产品期权定价的研究大多数仅限于理论研究阶段。就上述我国的两种农产品而言，其期权品种是美式期权，虽然已有文献中有关于美式期权定价对比分析方面的研究，但大都没有经过实际价格的检验，更没有基于我国农产品期权实际数据而进行的研究。本文通过比较B-S期权定价模型、二叉树定价模型以及蒙特卡洛模拟这三种方法，以我国新上市的豆粕期货期权为例，对我国农产品的期货期权的定价进行比较，并比较不同的参数选取方式对定价效果的影响，再通过与真实交易数据做比较，得出相对而言适合我国农产品期货期权的定价模型。

1 本文使用的期权定价的原理与模型

本文的期权定价模型主要分为三个。其共同点是都融入了期货保证金(m1)和期权手续费(m2)这两个因素。因为在实际的期货交易市场中，期货的购买并不是单纯的信用交易，作为合约的担保必须缴纳一定的保证金才能进行期货交易，而每个交易所都会有一定的标准来确定其保证金，也就是保证金率m1，且保证金在持仓者交割或者平仓后会返还给交易者，并且交易者再需支付一定的期权交易和行权手续费，即m2。因此，交易者也就损失了这个保证金的货币时间价值。而下面这3个模型融入了期货保证金和期权手续费，即将m1和m2融入模型中。

1.1 改进后的BAW模型

B-S模型的一大缺点就是不能很好地给美式期权定价，所以本文以Barone-Adesi和Whaley的BAW模型为基础，在BAW模型的欧式期权部分融入保证金率和行权手续费的因素。在BAW模型中，模型的解由两部分构成，一是同等B-S模型求出来的解，二是可提前行权而多支付的权利金。

对于第一部分，我们在求解B-S模型时所构造的资产组合的变化为：

(式1)

加入期货保证金之后，就相当于损失了保证金这一部分的利息，所以资产组合变为：

(式2)

原始B-S的偏微分方程为：

(式3)

在改进后的模型中融入了期货保证金这个因素，根据文章第二部分可得伊藤定理：

(式4)

结合伊藤定理，代入式3，得到改进后的偏微分方程：

(式5)

以C表示欧式买入期权的价值、P表示欧式卖出期权的价值、S为原生资产的价格、K为期权的执行价格、β为便利损失率、m1为保证金率，欧式期权定价的求解问题变为了以下方程：

(式6)

最后的看涨欧式期权部分定价模型变为：

C=e-(r-βm1)(T-t)SN(d1)-e-r(T-t)(K+m2)N(d2)

(式7)

根据期权的平价公式以及累计正态分布的性质，N(d)+N(-d)=1，可得出看跌欧式期权定价模型：

(式8)

对于第二部分可提前行权应多支付的权利金，因为：

VA(S,t)=VE(S,t)+e(S,t)

(式9)

所以，对于权利金e也需满足偏微分方程：

(式10)

而美式看涨和欧式看涨都满足：

VA(S,T)=max(S-K-m2，0)=VE(S,T)

(式11)

所以，e(S,t)必须满足：

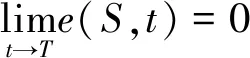
(式12)

当X(1-X)=0时，可以得到期权价格的精确值；当X(1-X)≠0时，上式则会变成:

(式13)

以上类似于一个常微分方程，其解的形式为aSρ，可得：

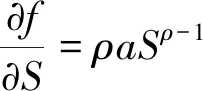
(式14)

(式15)

将式14和式15代入式13可得：

(式16)

解得：

(式17)

(式18)

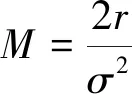
对于美式看涨期权来说，CA(S)满足如下公式：

(式19)

对于美式看跌期权来说，PA(S)满足如下公式：

(式20)

其中：

在以上CA(S)和PA(S)两个模型中，cE(S*)和PE(S**)是同等条件下欧式期权的解，A2和A1是美式期权比欧式期权需要多支付的那一部分权利金，S*和S**是期权执行的股价临界点。

1.2 改进后的二叉树模型

二叉树模型的一个优势就是既可以给欧式期权定价又可以给美式期权定价。步数越长，结果越精确。首先是单步二叉树的情形，期权的执行价格为K，若期货价格上涨，期权的价值为：fu=max(uS-K-m2，0)；若期货价格下跌，期权的价值为：fd=max(dS-K-m2，0)。构造一个组合，用Δ份的期货和无风险资产B来复制期权的价值，Δ和B都必须满足以下条件：

fu=Δus+rB-βm1

(式21)

fd=Δds+rB-βm1

(式22)

通过式21和式22可得：

Δ=(fu-fd)/(us-ds)

(式23)

Δs-f=e-rt(Δus-fu-βm1)

(式24)

(式25)

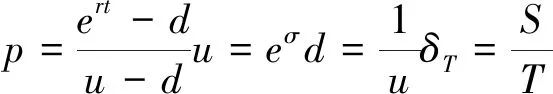
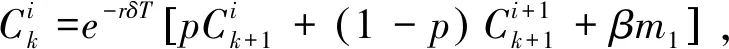
n步二叉模型的看涨期权公式为：

(式26)

n步二叉树模型看跌期权公式为:

(式27)

1.3改进后的LSM模型

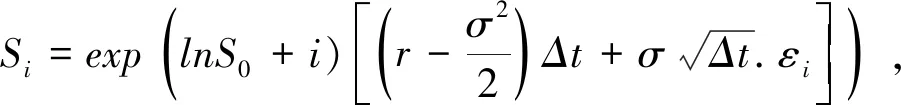
(式28)

2 实证分析

豆粕期货期权上市于2017年3月31日。本文以豆粕期货期权M1807-C等7个系列作为标的资产，分别为M1807-C2400、C2450、C2500、C2550、C2600、C2650、C2700。选取了2018年4月18日至2018年5月17日的数据作为样本数据。因虚值期权在进行模拟定价时不稳定，本文只选取了实值期权。根据期权代码可得，所选取数据合约月份为1807，C后面的数字为执行价格。

2.1 M1807豆粕期货的市场价格S

选取2018年4月18至2018年5月17日期间每个交易日的豆粕期货收盘价作为标的资产的价格S。例如，2018年4月18日交易代码为M1807的豆粕期货收盘价为3194。详情如表1所示。

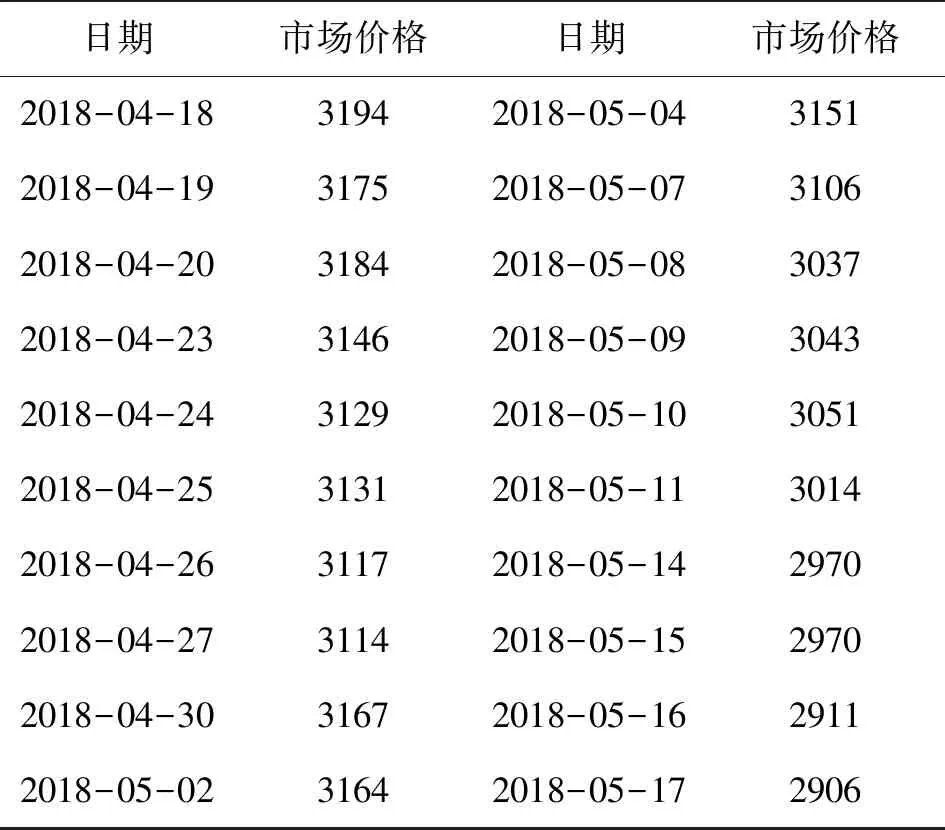
表1 豆粕期货2018-04-18至2018-05-17市场价格

2.2 M1807豆粕期货期权的执行价格K

根据以上期权的代码，可得所选数据的执行价格依次为2400、2450、2500、2550、2600、2650、2700这7个系列。

2.3 M1807豆粕期货期权的时间间隔T-t

所选取豆粕期货的数据月份为7个月，所以时间间隔T-t=07/12。

2.4 M1807豆粕期货的波动率σ

一般在波动率的选取上会考虑历史波动率和隐含波动率，因隐含波动率反映了投资者对未来波动率的预期，所以在本部分先选取隐含波动率。其数据在wind以及大连商品交易所可以直接获得。具体数据如表2所示。

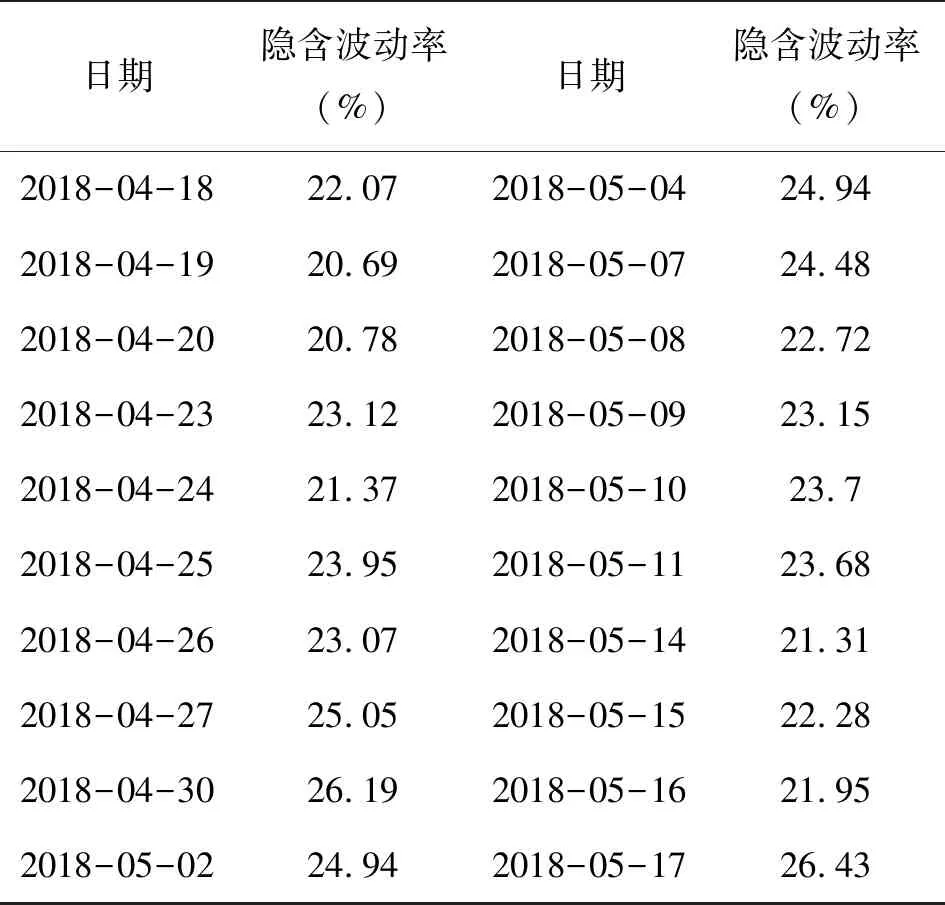
表2 豆粕期货期权2018-04-18至2018-05-17隐含波动率

2.5 M1807豆粕期货的无风险利率r

在计算中选用一年期定期存款利率1.5%，所以本文将1.5%作为无风险利率。

2.6 期货保证金率m1以及手续费m2的选取

期权交易手续费都可以通过大商所平台得到。2018年8月份之前交易手续费标准为1元/手，行权(履约)手续费也是1元/手；保证金的影响用便利损失率β*m1来表示(β一般情况下等于国债流动性损失，此处等于无风险利率1.5%，m1为保证金率，大连商品交易所规定豆粕的保证金率为7%)。

3 期权定价模型结果的比较分析

根据式10、式12以及式14这3个模型，利用Matlab编程可得到模型的预测价格，用Excel统计并绘制了对比图(见图1—图7)。每个图表示一种执行价格的豆粕期权的实际收盘价和模型拟合价格的折线图。

图1 M1807-C-2400真实价格与模拟价格走势

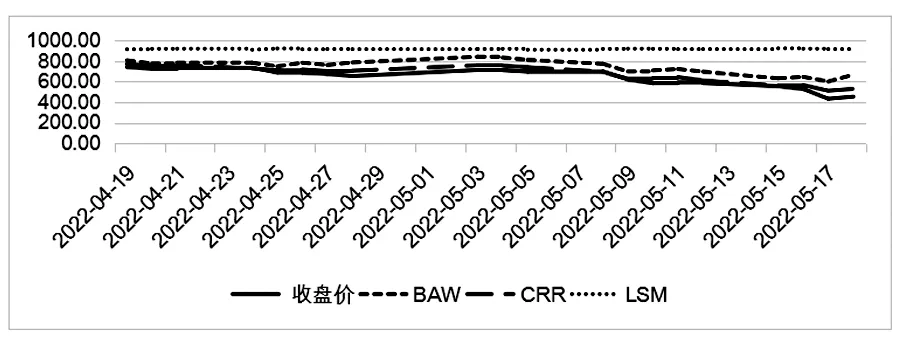
图2 M1807-C-2450真实价格与模拟价格走势

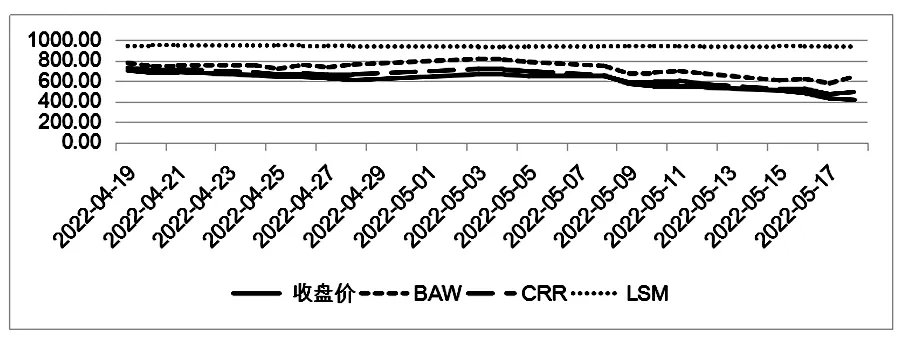
图3 M1807-C-2500真实价格与模拟价格走势

图4 M1807-C-2550真实价格与模拟价格走势

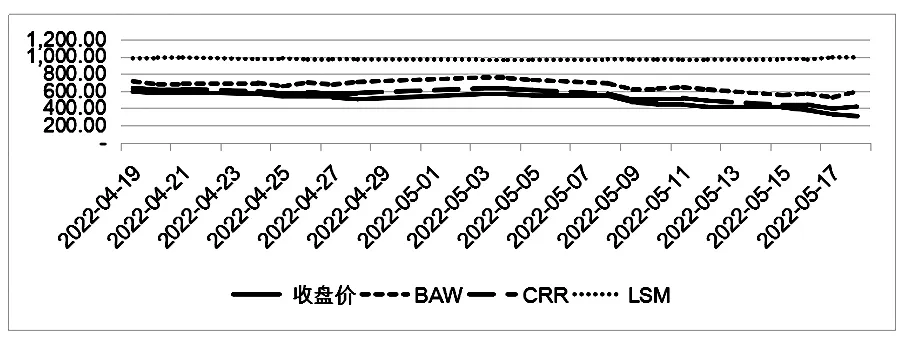
图5 M1807-C-2600真实价格与模拟价格走势

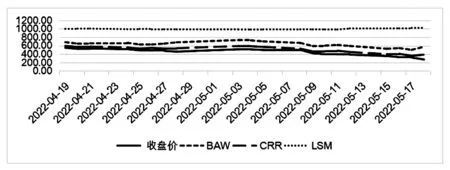
图6 M1807-C-2650真实价格与模拟价格走势

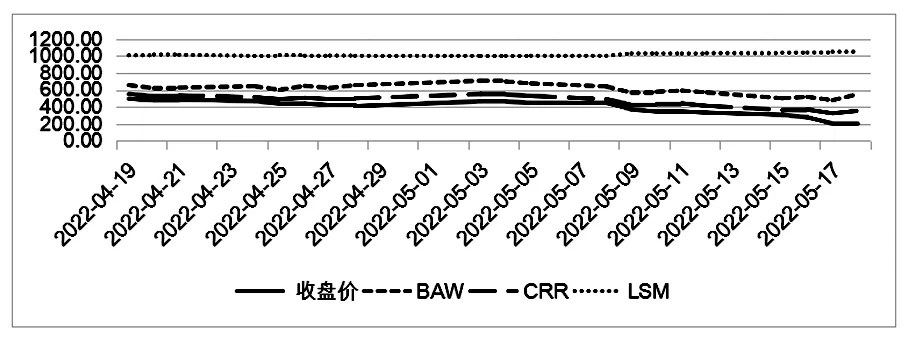
图7 M1807-C-2700真实价格与模拟价格走势

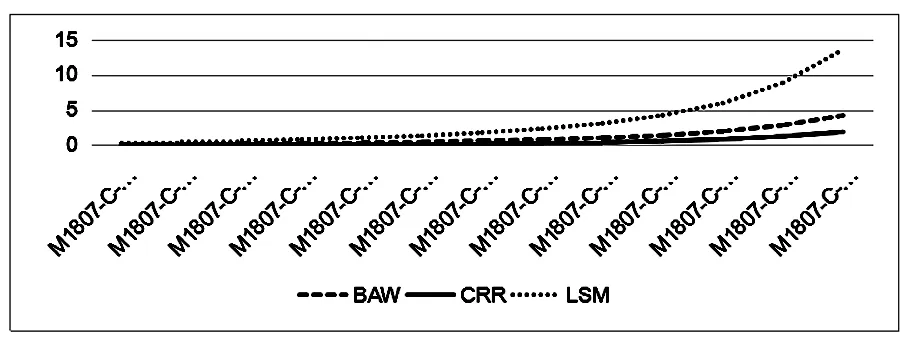
图8 不同期权定价方法的拟合精度比较

在比较定价结果时，为了进行定量分析，本文采用平均绝对比例误差(MAPE)来进行分析，Yabs，t表示实际收盘价格，Ypred，t表示用模型预测出来的价格：值越小，意味着模型模拟较好；值越大，说明模拟较差。其定义为：

由图1—图7可知：(1)期权每一日的收盘价随着执行价格的上升而上升，BAW和CRR的这种趋势与收盘价是一致的，而LSM的趋势与收盘价相反；(2)随着执行价格的提高，LSM与真实价格之间的距离越来越远，严重高估了豆粕期货期权的价格，说明LSM的定价误差越来越大。根据不同期权定价方法的拟合精度比较(见图8)可知，BAW与CRR的定价误差较小，总体呈高估的态势，几乎接近于真实价格，但是也会随着执行价格的升高误差而有所增加，这说明CRR更接近于我国豆粕期货期权的真实价格。

4 结语

考虑到豆粕期权的手续费和保证金的因素，其模型比一般的模型在假设条件上要有所放宽,且融入保证金和手续费因素的模型比改进之前的美式期权模型的误差要小;在使用工具上，使用Matlab编程来进行模型的求解，所以在模拟价格的获取上更加简单，并且在进行结果统计部分使用Excel，其使用比较普遍，操作起来更加容易；通过对比三个模型的模拟价格与实际价格发现，CRR与BAW模型与实际价格变化趋势一致，误差控制在10%左右，差异可以接受。