智能制造中RFID区域碰撞问题的研究与改进

王 琪，王 涛，朱 青，邢 燕，陈金环

（山东建筑大学 信息与电气工程学院，济南 250101）

0 引言

智能制造（Intelligent Manufacturing，IM）是由智能机器和人类专家共同组成的人机一体化智能系统。大力发展智能制造产业既符合我国制造业发展的内在要求，也是重塑我国制造业新优势、实现转型升级的必然选择。

智能制造的显著特点是柔性制造和高效生产，这就需要对设备和原材料等数据的准确高效提取。目前国内大多数制造企业采用条形码采集相关数据，识别效率不高，已无法满足当前制造业的需求。而RFID技术的出现大大地提高了识别效率使该问题得到了解决。

所谓RFID，指的是射频识别技术（Radio Frequency IDentification），它通过空间耦合的方式识别电子标签内的信息，实现阅读器与电子标签的数据交换。工业现场作业量大、流动性强，在同一阅读器的识别范围内，常会出现多个标签同时向阅读器发送信息的情形，这就是标签碰撞，此时数据信息间相互干扰，标签数据无法被正确读取。

现有的RFID标签防碰撞算法中性能较好的是动态帧时隙ALOHA算法，它在一定程度上提高了系统的识别效率，但该算法仍存在较大的随机性，存在标签饥饿问题。此外，以二进制搜索算法为代表的确定性防碰撞算法虽然解决了标签饥饿的问题，但却以系统复杂度高为代价，不适用于高实时性要求的工业现场。针对上述问题，本文提出了一种改进型分组动态帧时隙ALOHA算法，有效提高了系统吞吐率的同时，节约了系统成本，可用于智能制造工业生产线中。

1 传统ALOHA算法

ALOHA算法是根据RFID系统的特点不断改进形成的算法体系，它的本质是分离标签应答的时间[1]，即当标签进入阅读器的读取区域后，在不同时间响应阅读器的命令。若同时有多个标签响应阅读器的命令，会发生标签碰撞，标签碰撞分为两种情况：一种是部分碰撞，另一种是完全碰撞，如图1所示。

图1 标签碰撞示意图

发生碰撞了的标签都无法被阅读器识别，此时阅读器会发送命令让这些标签转入待命状态，随机等待一段时间后再重新发送应答信号。

1.1 纯ALOHA算法

纯ALOHA算法是指标签在发送应答信号时可以任意选择响应时间，不需要同步各个标签的响应时间。这种算法简单易行，但随着电子标签数目的增多，发生标签碰撞的可能性增大，系统识别效率不高，近年来工业生产线中已渐渐淘汰这种算法。

1.2 帧时隙ALOHA算法

帧时隙ALOHA（Framed Slotted ALOHA，简称FSA）算法是对纯ALOHA算法的一种改进，其核心思想是将数据帧离散成若干个帧时隙，待识别的标签随机选择帧中一个时隙响应阅读器的命令，以数据帧为周期进行数据交换。

若一个时隙仅被唯一标签选中，则此标签被成功识别；若一个时隙被多于一个的标签选中，就会产生标签碰撞现象。碰撞的标签将在下一个帧中随机地选择一个时隙重新发送信息，整个算法过程都会如此循环，直到所有的标签均被识别。FSA算法工作过程如图2所示。

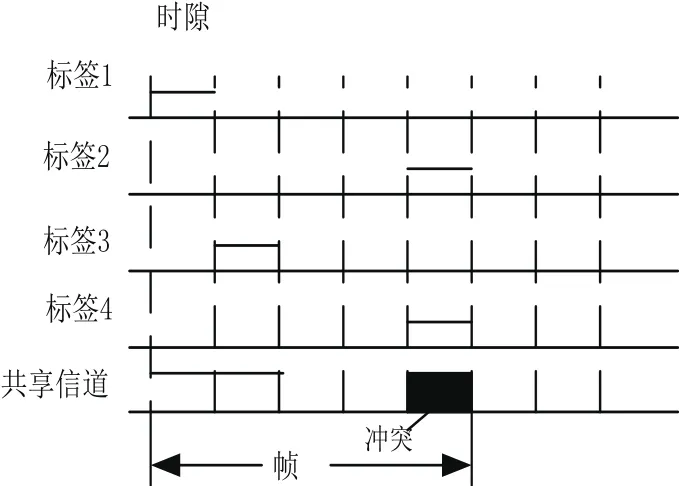
图2 帧时隙ALOHA算法工作过程示意图

设数据帧有N个时隙，待识别标签个数为n，同时有r个标签选择同一时隙的概率服从二项式分布定理[1]：

由式(1)知，一个时隙仅被一个标签选中的概率，即标签被成功读取的概率为：

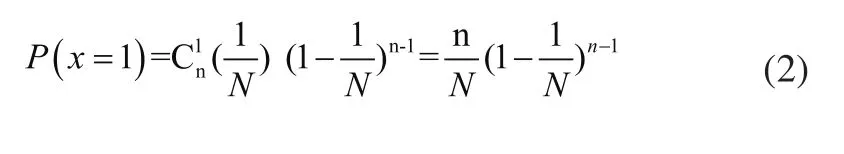
由此可以推算，一个数据帧内成功读取标签的时隙数为：

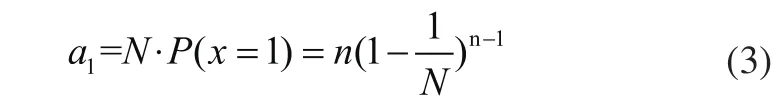
此时系统的吞吐率（识别效率）为：

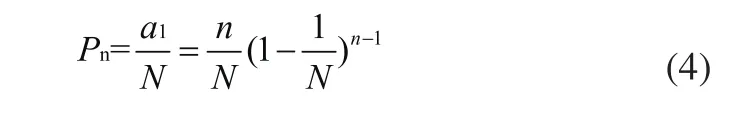
为使系统获得最优性能，对式(4)求导：

可以得出：

将上式进行变换：

当n很大时，将上式做泰勒级数展开：

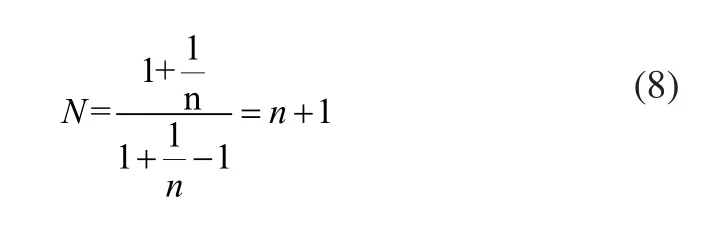
上述推导表明：标签数目与数据帧长度大致相等时，系统取得最优性能。当标签数目远大于数据帧长度时，发生标签碰撞的可能性增加；当标签数目远小于数据帧长度时，造成时隙浪费。因此希望阅读器能够根据标签数量动态调整数据帧的长度，提高RFID识别系统的稳定性。

1.3 动态帧时隙ALOHA算法

动态帧时隙ALOHA（Dynamic Frame Slotted ALOHA，简称DFSA）算法能够动态改变数据帧的长度，使之始终与待识别的标签数目大致相同，使系统具备最优性能 。但是，工业现场作业量大，肯定会出现标签数目远大于数据帧长度的情况。由于硬件条件的约束，数据帧的长度不可能无限增大（最大长度为Mmax=256）[2]。针对这一问题，本文提出将工业现场待识别的标签分组，每次阅读器仅对一组标签进行识别的方案，同时根据每轮统计所得碰撞时隙数动态改变数据帧的长度，使系统具备最优性能。

2 改进型算法性能分析

本文采用的算法延续了DFSA算法的优点，并根据将待识别标签数量估算值进行分组；此外，同时开始四个时隙接收信号，根据统计所得碰撞时隙数来动态改变数据帧的长度。

2.1 待识别标签数目估算与分组

系统获得最优性能时，数据帧中一个时隙中发生标签碰撞的概率为ε=0.4180[3]，则一个时隙中发生标签碰撞的标签的个数为：

在正式进行标签识别前，系统首先要对标签进行一轮快速识别，统计本轮识别中碰撞时隙数为C0，则待识别的标签总数为：

求得的待识别标签总数n后，考虑是否对电子标签进行分组，限制每次参与应答的标签的数量，使之与当前数据帧的长度相匹配。

根据式(4)，将两条吞吐率曲线交点处的标签数量，作为阅读器调整帧长的临界值[4]。即：

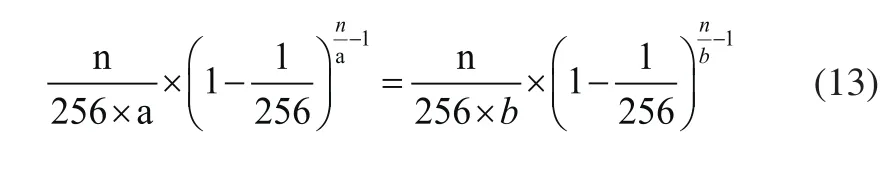
其中，a，b为标签的分组数，设a取1，b取2，代入式(13)得：

可以求得标签数目分组的临界值为：

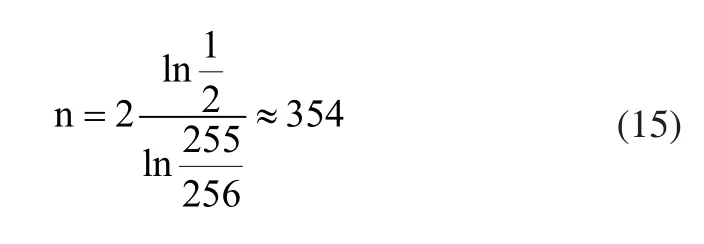
若已知待识别标签数目为n，当n＜354时，不对标签进行分组；当354＜n＜610时，将标签分为两组：一组包含256个标签，另一组为剩余标签；当610＜n＜866，则将标签分为三组：其中两组的标签数为256，另一组为剩余标签；以此类推。

另一方面，阅读器设定的数据帧长度一般为二的幂次方，如16、32、64、128、256。故不同范围的标签数目n相对应的帧长度如表1所示。

表1 不同标签个数对应的帧长度和分组情况

2.2 改进型算法过程描述

本文所采用的算法中，阅读器首先选定一组标签为当前组，并根据该组标签的数目，决定初始时隙范围参数Q（取值范围为0～15）的值，随后生成长度为2Q的数据帧。选定的初始时隙范围参数Q应满足使当前数据帧长度与当前组待识别标签数目大致相同。

随后，阅读器向所有当前组标签发送带有参数Q的请求响应命令Query（Q），标签收到Query命令后做出响应，由标签自带的随机数生成器T生成一个[0，2Q-1]范围内的随机数作为时隙值并储存在自身的随机数储存器S中。

然后，阅读器发送一条包含时隙请求参数R（R=0）的命令开启第R 组时隙接收信号[5]。

时隙值在[4×R，4×R+3] 范围内的标签响应此命令，返回一个16位的随机数N16；若当前时隙只有一个标签响应，阅读器成功与标签建立通信，向标签发送确认命令，被正确识别的标签将自身的EPC数据发送给阅读器；若当前时隙有多个标签响应，阅读器收到多个标签发送的随机数发生信息碰撞，则将该时隙标记为碰撞时隙；若当前时隙无标签响应，则标记为空闲时隙。

阅读器识别完一组时隙后，自动将R值加一，跳转到下一组时隙的识别过程，继续发送请求响应命令，如此循环。识别完当前组所有标签后，阅读器统计本轮识别过程中空闲时隙、成功时隙和碰撞时隙的数量，分别记为C0、C1和C2；根据统计结果动态调整当前组下一轮识别过程的帧时隙数。设当前帧时隙数为M=2Q，调整方法如下：

1）如果C2≥0.7M，则将下一轮识别过程的帧时隙数调整为2M=2Q+1，即随机数Q的值加1；

2）如果C2＜0.7M，则下一轮识别过程的帧时隙数依然为M=2Q，即随机数Q的值不变；

3）如果C2≈0，则将参与下一轮识别过程的帧时隙数调整为0.5M=2Q-1，即随机数Q的值减1。

根据上述1）、2）、3）方法动态调整当前组数据帧的长度，直至某次识别过程中没有一个标签被识别，则认为当前组所有标签具备识别，系统跳转到下一组的识别过程。

3 仿真分析

取标签个数n的范围为0～1000，通过对比标签个数为不同值时所需要的总时隙数和吞吐率，比较FSA算法、DFSA算法与本文提出的算法的性能优劣。其中，FSA算法中帧长取定值为256，DFSA算法的帧长度选取原则如表1所示。本文进行了100次仿真取其平均值。

由图3可以看出，当标签数目0～256的范围内时，3种算法的所需的时隙数大致相同，而随着标签个数的增加，FSA算法和DFSA算法所需的时隙数呈指数增加，本文算法所需的时隙数呈线性增长。主要原因是当标签数量巨大时，本文算法能根据碰撞时隙的数目动态的改变数据帧的长度。可见本文提出的算法能够显著减少识别所需的总时隙数，从而减少识别总耗时，提高系统的识别效率。

图3 标签个数为不同值时需要的总时隙数对比

由图4可以看出FSA算法与DFSA算法的吞吐率都不高，不超过百分之三十五，而本文提出的算法的吞吐率稳定在百分之四十五，可见本文算法有效地提高了系统的吞吐率；此外，当标签数目超过一定限值时，FSA算法和DFSA算法的吞吐率急剧下降，而本文算法的吞吐率能基本保持稳定，从而保证了系统性能的稳定。

仿真结果表明，本文提出的算法系统吞吐率最高可达48%，提高了干扰环境下多标签系统的读取效率，本算法可以有效运用于工业现场的RFID系统中。

4 结束语

即根据待识别标签数目的估算值选择初始时隙参数Q的大小，同时开启四个时隙接收信号，并根据每轮统计所得碰撞时隙数有针对性地改变下一轮数据帧的长度。仿真结果表明，本算法吞吐率最高可达48%，且当标签数目逐渐增多时，本算法性能较稳定，可以有效运用于智能制造工业现场的RFID系统中。

本文在DFSA算法的基础上提出一种改进型算法，

图4 标签个数为不同值时系统的吞吐率对比