基于优化模拟退火算法的航天薄壁结构件车间布局优化

彭劼扬，王家海，沈 斌

（1.同济大学 机械学院，上海 201804；2.同济大学 中德学院，上海 201804）

0 引言

航天产品加工过程复杂，大多数加工生产都是根据工艺人员的经验进行设施规划和加工，生产效率低下。在提高生产效率的方面，设施布置设计被视为提高车间生产力的关键[1]。研究表明，20%～50%的操作费用是用于原料运输费用中。而工厂布局属于NP问题，使用数值计算方法很难高效地解决，目前大都使用启发式算法[2]或使用计算机软件仿真进行求解。

对于布局问题，国外最早于1961年由Richard Muther研究出系统布置设计SLP方法，首次提出对于相互作用的生产单元之间的关系表示法，对后续相关研究打下坚实的基础[3]。随着科技的发展，SLP的缺点渐渐凸现出来，科研人员开始使用启发式算法和SLP相结合的方式，衍生出改进法[4]。Ravi Kothari和Diptesh Ghosh[5]提出使用两个禁忌算法对单行设施布局进行实现的策略，其中一个禁忌算法是穷举搜索的2-opt邻域，而另一个涉及插入邻域的穷尽搜索，能够加快两个邻域的搜索。齐继阳和竺长安[6]使用改进型模拟退火算法，使用禁忌表的手段，增加了退火算法的记忆能力。庞峰[7]将改进SA算法应用到板式家具问题上，使材料利用率普遍高于95%。

基于以上研究，本文主要对对设备布局算法进行研究，提出了混合算法的一般设计原则。通过对比分析，发现将模拟退火思想应用到遗传算法中能提升算法的收敛性，减少迭代次数。并在此基础上，应用Plant Simulation仿真软件对某航天大型零件车间布局进行仿真，验证了混合算法的优越性。

1 数学模型

本文是对块状工位进行研究，对于块状的工位，需要考虑到一个设备所需的运维面积及该工位所需的工位面积。给定长×宽的时候，进行布局，则每一行的宽度由该行中最大宽度设备块决定。布置过程如图1所示，其中单行布置可以看成多行布置的特殊形式。

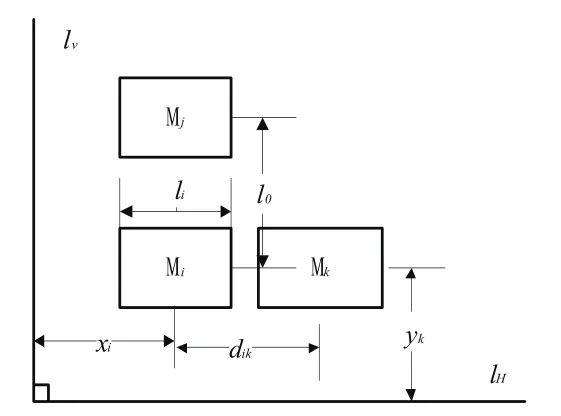
图1 设备布局

而相应的数学模型可以表示如下：

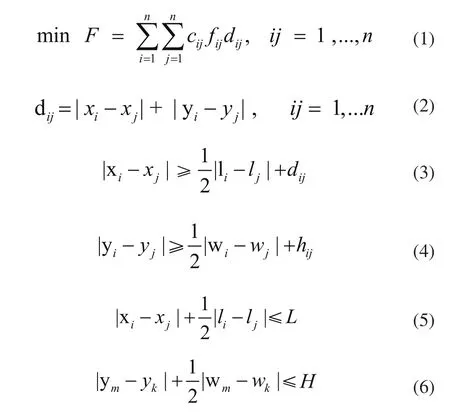
其中：F是目标函数值；Cij为物料运输费用；fij为物料运输量；dij为两个设备之间的距离；xixj为两个设备之间x坐标值；yiyj为两个设备之间y坐标值；lilj为设备i，j的长度；wiwj为设备i，j的宽度；L，H分别为车间的总长度和总宽度。

式(1)中，以物流量为优化目标，能够很大程度上达到对车间的布局优化；式(2)中，dij作为两个设备之间的距离，设备之间通常不能直接接触的，距离的大小是通过两个设备块中心之间的直线距离进行衡量的；式(3)中主要是对同一行中两台设备在X轴方向进行限定，保证两台设备不交；式(4)中则是不同行相邻设备之间在Y方向上不能交叉；式(5)是对车间长度方向的约束，不能超过车间规定的总长；式(6)是在车间宽度方向进行的限制，不能超差。基于以上公式的约束可以保证建模的合理性。

2 混合算法的设计

算法间存在多种结合方式，但是并不是所有的结合方式都能使新算法优于单个算法，因此对于两个算法的结合应遵循以下原则进行：1）算法优缺点结合原则：相结合的两个算法能够优缺点互补，如此混合算法将优于独立算法。或者尽量减少两个算法缺点的相同部分，从而减小了对混合算法在该部分的进一步弱化；2）解形式一致原则：在算法结合过程中，注意解的联系，两个算法的结合部分注意解的形式的变换，如：遗传算法中采用的是编码的方式进行计算的，但是在粒子群算法中采用的是粒子的方式，在形式上有所区别。3）遵循适用原则：在处理具体问题的时候，有些算法不适合解决该问题的时候，就不能再使用该算法与其他算法进行结合来解决问题。

本文对于模拟退火遗传算法进行的结合能够同时满足以上原则，能够进行算法融合，混合算法流程如图2所示。

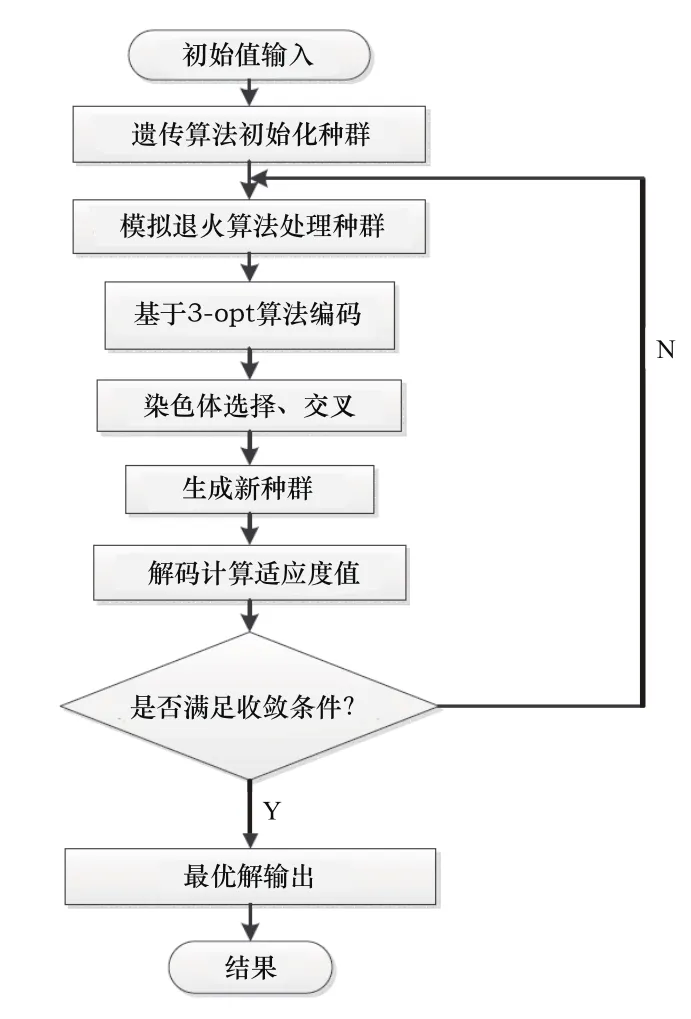
图2 混合算法流程

算法描述如下：

1）首先设置参数，种群数量，迭代次数，交叉率，变异率，初始温度等；

2）采用退火原理对初代进行处理；

3）使用遗传算法进行选择、交叉、变异，方式如上文所述；

4）计算适应度值，进行比较，产生下一代种群；

5）产生子代后，若满足收敛条件则输出最优解，否则继续进行迭代操作直到找出最优解。

3 混合算法的实例验证

多行布局中在进行坐标求解时，按中心点的X坐标和Y坐标进行表示每个设备的位置。本算例采用文献[8]中某机械加工企业，车间内设备的摆放方式是以机群为主。而且在其中生产的产品的质量较大，因此车间物流量相对较大。该车间是一个长为20m的正方形形状车间，进行产品加工的设备有10台，物流成本如下所示：

设备长度：{4.3，4.3，4.65，2，5，3.5，1.8，3.85，5，5}；

设备宽度：{5.6，3.7，7.75，4，4.2，5，2，4，4，4}。

单位成本矩阵如表1所示。

表1 费用矩阵

车间的初始布局为{1，2，3；4，5，6；7，8，9，10}，此时车间运输成本为3748.8元。本文选取算法种群大小为10，子代数目为8的情况下，最大代数迭代到100，交叉率为0.8，变异率为0.2。

表为三种算法运行结果对比如表2所示。

表2 算法结果对比

多行布局平均值收敛曲线如图3所示，其中横坐标为迭代次数，纵坐标为物流运输当量值，即是前文所述目标函数值。

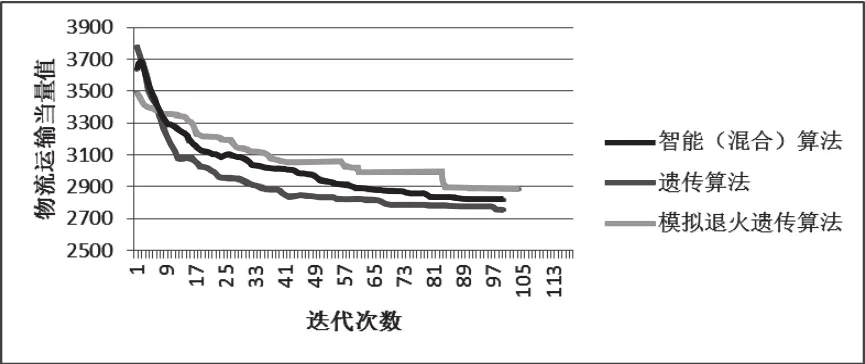
图3 10次平均值迭代曲线

收敛曲线如图4所示。

求解结果分析：

1）图4中可知，10次混合算法平均解的收敛速度明显高于遗传算法和模拟退火算法。混合算法的10次解中只有第四次和第五次的解比遗传算法稍差，其他的解均优于遗传算法，而混合算法十次解中均优于模拟退火算法的解。

2）根据图3中对比可以看出，混合算法的结果明显优于其他另外两种方式，混合算法在30代左右收敛到最好结果，而其他两个算法在40代以后得到最终结果，且最优解相比混合算法较差，因此，混合算法的收敛特性和最优解均优于单独算法。

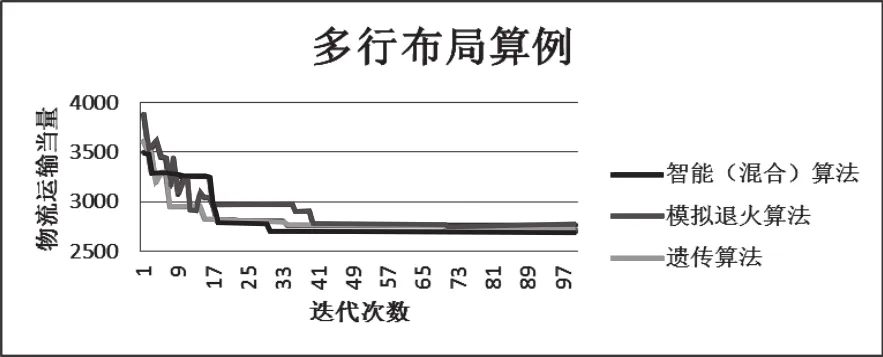
图4 最优解收敛曲线

4 基于Plant Simulation的布局算法仿真

航天薄壁结构件生产车间的情况较为复杂，涉及多品种小批量的混流生产，本文验证的车间生产两种型号的火箭储箱，其中产品A是由6个筒段和2个箱底组成，而产品B是由6个筒段和2个箱底组成，年产量为12个贮箱。

使用Plantsimulation仿真软件进行二维仿真，由混合算法得出的结果得出布局方案，如图5所示，优化后的布局为（1，2，3；5，16，4，9，13，7，15，12；14，10，8，11，6），在Plant Simulation构建二维及三维仿真模型如图5所示：

图5 车间二维、三维布局图

图6 仿真运行结果

由仿真结果可知，生产相同产品的情况下，经过布局优化后的车间加工时间大大缩短，图5所示经过改进后的仿真运行结果：

由图6可知，在生产同样零件个数的情况下，加工时间由365天缩短到204天左右，生产效率极大的提高了。

5 结束语

本文主要对现有航天产品车间进行改造，通过对布局算法的研究，分析遗传算法和模拟退火算法从而设计出混合算法，并进行了算法验证，得出了算法的有效性。通过混合算法对车间布局进行求解，获得了车间布局优化方案。仿真结果表明：该混合算法具有很好的收敛特性，同时能够得出较为理想的结果。