二极管钳位式三电平逆变器功率管开路故障诊断

王福忠，曹 斌，韩素敏，冯文成

（河南理工大学 电气工程及其自动化学院，焦作 454000）

0 引言

二极管钳位式（neutral-point-clamped，NPC）三电平逆变器因输出容量大、输出电压高、电流谐波含量小等优点而广泛应用。相比于传统的两电平逆变器，NPC三电平逆变器每一桥臂由更多的功率管和二极管组成，结构更加复杂，这使得功率管发生故障的概率增加。功率管的开路故障一方面是由于过流烧毁导致开路，另一方面是由于驱动连接不良、线路断裂引起的驱动信号开路[1]。文献[2,3]取故障相电压的大小作为故障特征，定位出故障开关管，但选取单一的故障相电压特征只能诊断出单管故障，对于复杂的多管故障无法诊断，可靠性不高。文献[4～6]采用专家规则方法对单管故障诊断，神经网络方法对双管故障诊断，在实际中并无法提前得知逆变器具体的故障类型，因此单管故障与双管故障分开诊断的方法并不可靠。文献[7]用BP神经网络的方法仅对一相功率管故障进行诊断，而且BP神经网络具有收敛速度慢，易陷入局部最优等缺点。文献[8]意识到BP神经网络的缺点正是粒子群算法的优点，采用了改进粒子群算法对三电平逆变器两只功率管故障进行了诊断，但是对于单个功率管的故障无法诊断。为了提高NPC三电平逆变器故障诊断的可靠性，本文提出了一种基于杂交粒子群算法优化BP神经网络的故障诊断模型，该模型能够同时诊断NPC三电平逆变器的单个功率管开路与两个功率管开路的故障，同时利用杂交粒子群算法优化BP神经网络，提高故障诊断的精度。

1 NPC三电平逆变器的开路故障分析

NPC三电平逆变器主电路由直流电压电源、三相三电平桥臂及负载组成，拓扑结构如图1所示。

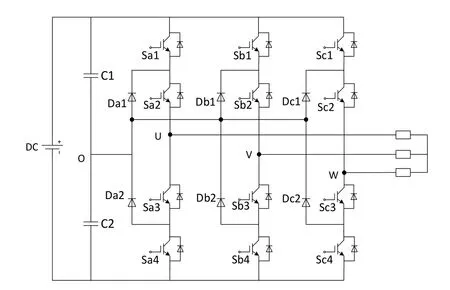
图1 NPC三电平逆变器拓扑结构图

鉴于电路的对称性，以A相为例，当三电平逆变器工作在正常情况时，A相的输出电流波形如图2所示。

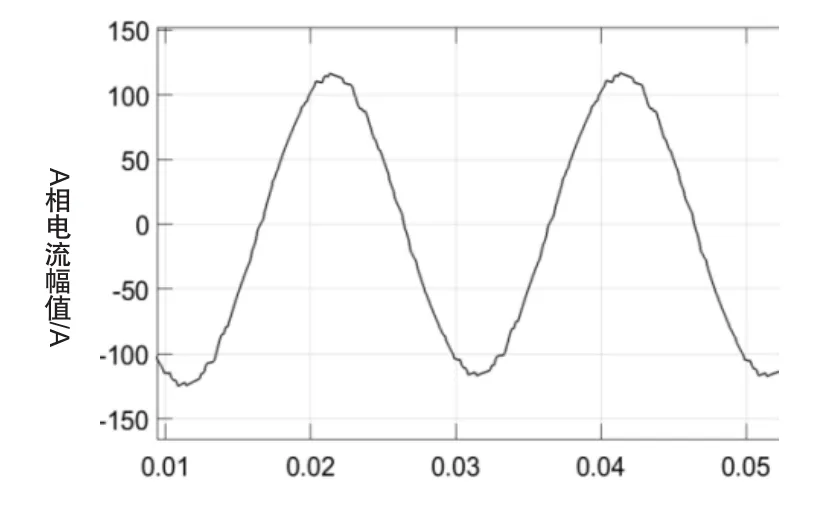
图2 无故障时A相输出的电流波形

NPC三电平逆变器故障组合数目众多，故障情况比较复杂。由于实际中多个功率管同时发生故障的几率很小，所以本文假设最多有两个功率管同时开路。所有的故障类型如表1所示。前两类称为单相故障，共计30种；第三类称为两相故障，共计48种，所有故障共计78种。

表1 NPC三电平逆变器开路故障分析

1.1 NPC三电平逆变器单相故障

发生单相故障时，故障相输出电流有明显畸变。以A相为例，当Sa1发生开路时，输出相电流波形如图3所示。负半周幅值不变，正半周幅值为正常值的1/2。

图3 Sa1开路时输出电流波形

当Sa4发生开路时，正半周幅值不变，负半周幅值为正常值的1/2，波形与Sa1发生故障时的波形关于0轴对称，相位相差180°。当Sa2发生故障时，输出相电流波形如图4所示。负半周幅值不变，正半周幅值基本为零。Sa3发生开路时，正半周幅值不变，负半周幅值几乎为零，波形与Sa2发生故障时的波形关于0轴对称，相位相差180°。

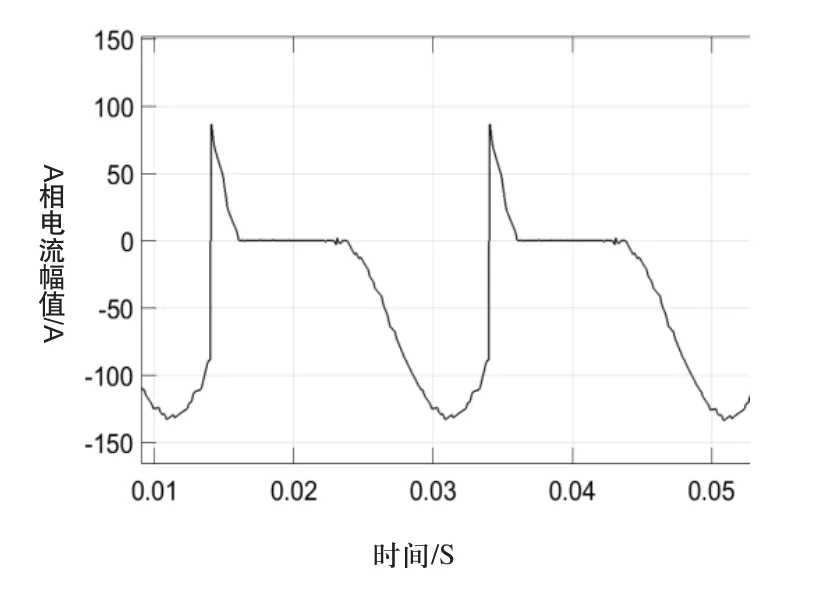
图4 Sa2开路时输出电流波形

仿真时发现，Sa2单独开路与Sa1和Sa2同时开路具有相同的输出波形。同样Sa3单独开路与Sa3和Sa4同时开路具有相同的输出波形。此时先按单管发生故障处理，在更换新的功率管后再判断Sa1或Sa4是否发生了故障。

1.2 NPC三电平逆变器两相故障

两相故障是指不同桥臂上两只开关管故障，即Sim与Sjn共同发生故障，其中i，j=a，b，c，（i≠j）。m，n=1，2，3，4。

共有48种情况。首先，将采样三相电流输出波形，然后利用d-q变换对其降维处理，变换公式如式(1)所示：

NPC逆变器中输出信号具有周期性，可以运用傅立叶变换对Id和Iq进行分析，将时域中的故障波形变换到频域，以突出故障特征。图5为Sa1与Sb2同时发生开路时Id的波形，图6为使用MATLAB中的FFT函数对Id进行分析得到的频谱图，得到各次谐波的幅值和相角。

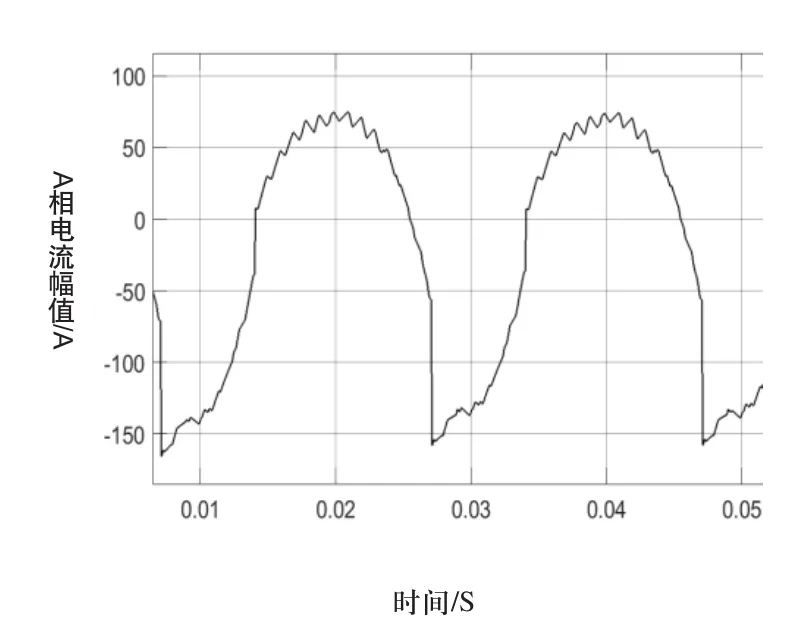
图5 Sa1和Sb2开路时的Id波形

图6 Sa1和Sb2开路时的频谱图

由图6可知，Id和Iq采集信号的直流分量及前两次谐波的幅值和相位基本上就包含了进行故障时别的各种信息。因此，分别对Id和Iq的波形进行傅里叶变换，取各自的直流分量、基波幅值、基波相位和二次谐波相位这八个参数作为故障特征信号。此外，当发生对称故障时，即Sa4和Sb3开路时，Id的波形如图7所示。图5与图7波形沿0轴对称，相位相差180°，数学关系如式(2)所示：

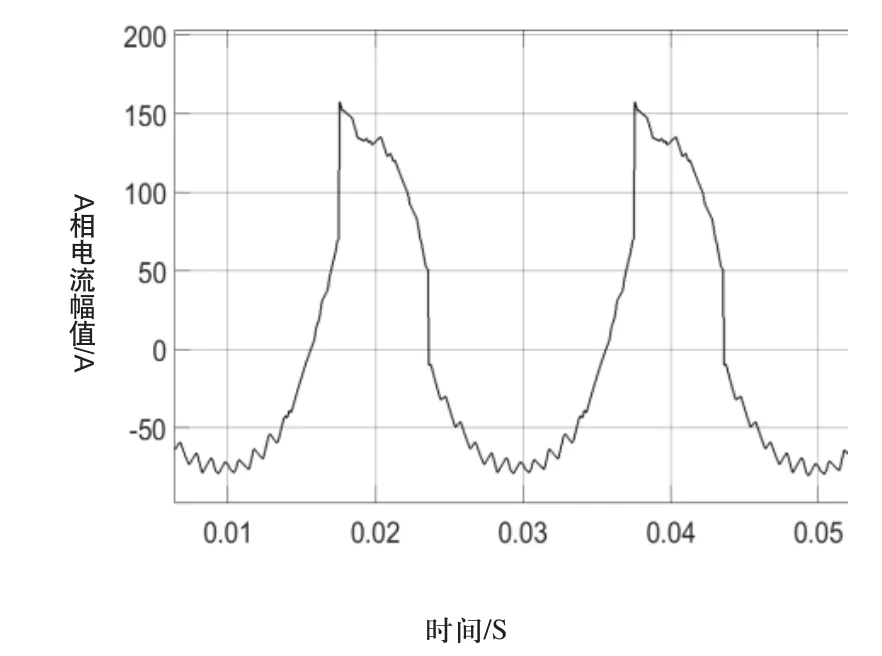
图7 Sa4和Sb3开路时的Id波形

文献[9]已作出数学证明，发生对称故障时奇次谐波相位相等，偶次谐波相位相差，各次谐波幅值相等，总的谐波畸变率（THD）相等。

2 基于BP神经网络的NPC三电平逆变器故障诊断模型

2.1 故障特征表的建立

利用七位二进制数Y7Y6Y5Y4Y3Y2Y1对三电平逆变器故障的所有情况进行编码。Y7为0时表示逆变器发生了单管故障，为1时表示发生了两管故障。Y6、Y5、Y4分别代表A、B、C三相，为1表示该相有功率管发生开路故障，为0时表示该相无故障。为了减少神经网络对样本学习的复杂性、提高诊断的正确性，对称故障的Y6Y5Y4Y3Y2编码相同，Y1用0和1来区分。表2为输入电压为400V，负载功率为40kW时的故障特征向量表，由于篇幅所限，仅列出故障特征表的一部分。从表2中可以看出，发生对称故障时奇次谐波相位相等，偶次谐波相位相差，各次谐波幅值相等，从而验证了仿真结果的正确性。

2.2 神经网络的设计

NPC三电平逆变器输出的电流经傅里叶变换后构造的特征向量与故障编码之间存在非线性逻辑关系，很难建立它的精确数学模型。通过神经网络可以建立故障特征向量和故障类型之间的对应关系，是目前用于故障诊断时一种十分有潜力的方法。

对BP神经网络设计时，首先要选择网络层数。输入向量为Id和Iq的直流分量、基波幅值、基波相位以及二次谐波作为神经网络输入，故输入层个数为8。输入层和隐含层之间的神经元采用tansig函数。隐含层个数没有明确规定，利用经验式(3)来确定：

其中，m为隐含层个数，n为输入层个数，则隐含层个数为17。输出为七位二进制，因此输出层节点数为7，输出层和隐含层之间的神经元采用Sigmoid函数。BP神经网络的结构如图8所示。

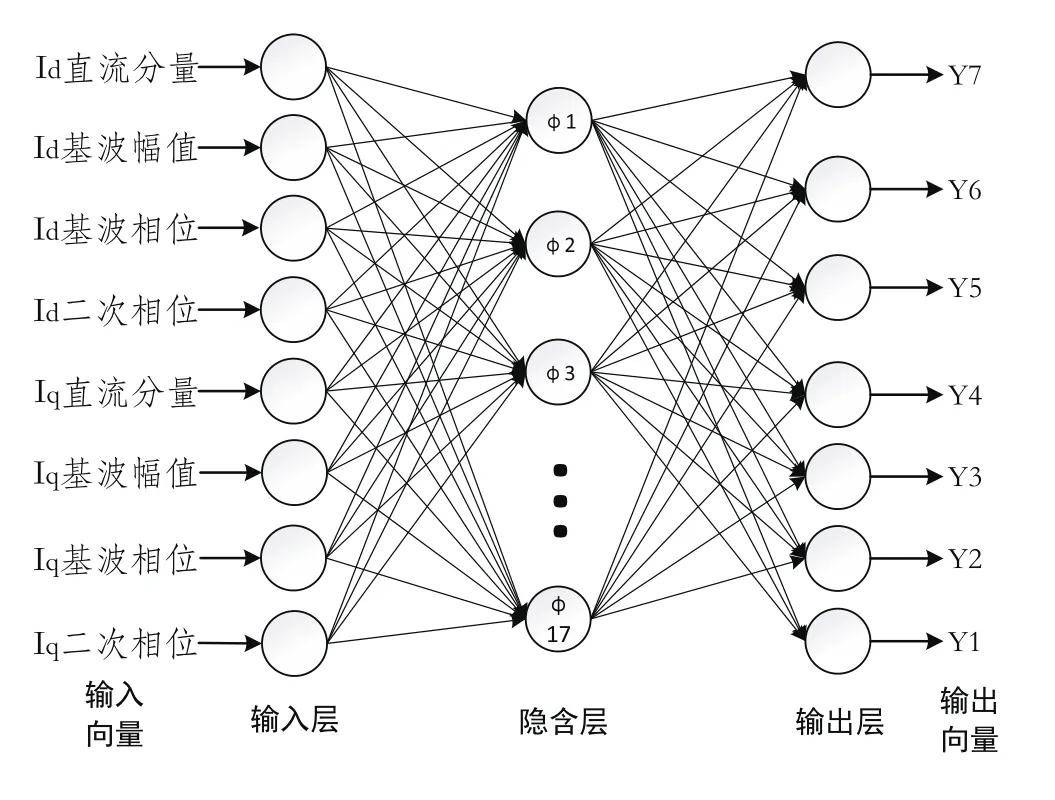
图8 BP神经网络的结构图

3 BP神经网络的优化

BP神经网络具有良好的泛化能力，可以逼近任意的非线性映射关系，但缺点是易陷入某些局部最小值，或者在这些点之间振荡。这种情况下无论进行多少次迭代，系统都存在很大误差，因此需要对神经网络进行优化，跳出局部最小值。

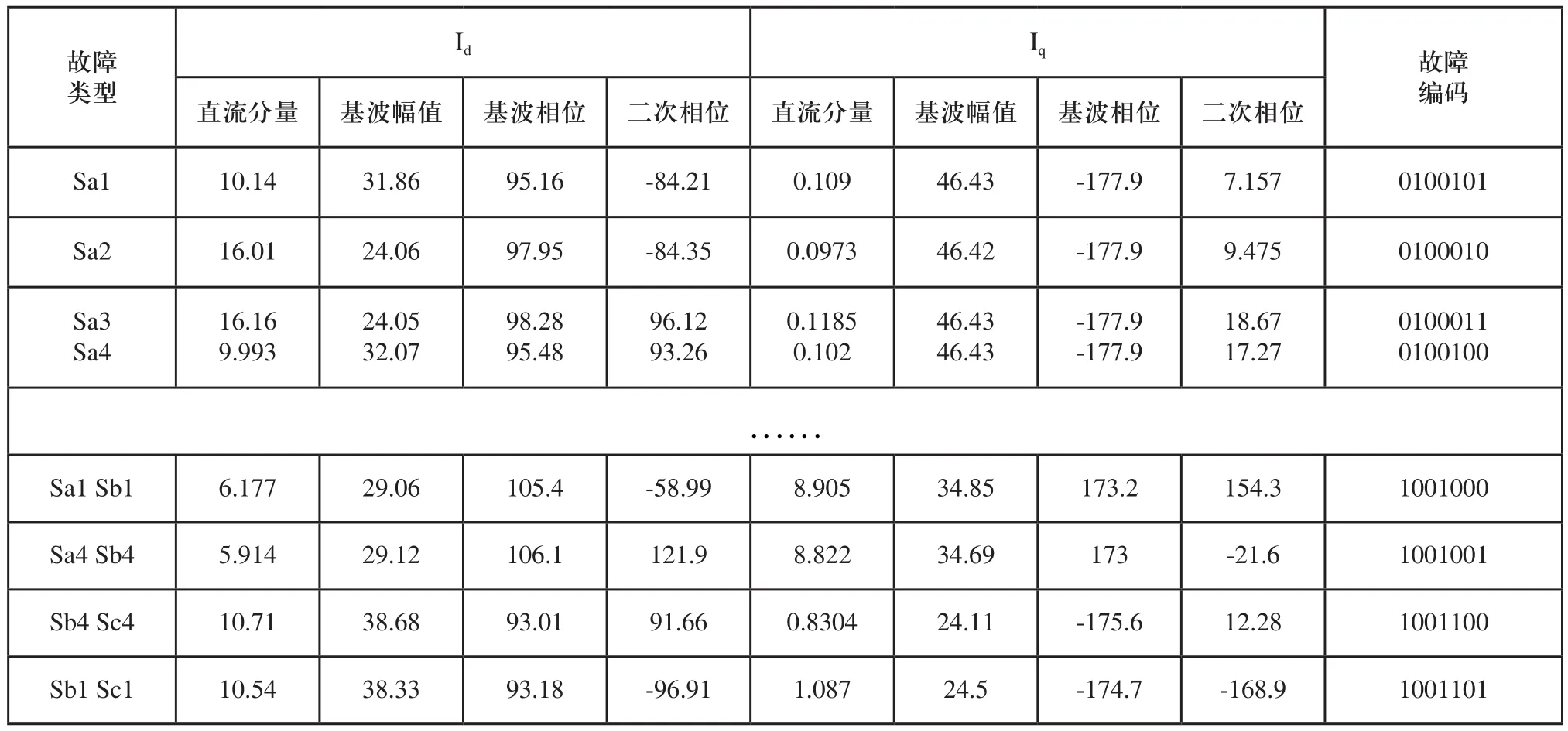
表2 故障特征向量及其编码

3.1 基本粒子群算法

粒子群算法（PSO）是一种基于群体的优化算法，基本思想是随机初始化一群没有体积、没有质量的粒子，每个粒子视为优化问题的一个可行解，粒子的好坏由适应度函数来确定。每个粒子将在可行解空间中运动，并由一个速度变量决定方向和距离。通常粒子追随当前的最优粒子，通过迭代找到最优解。用pbesti表示粒子个体历史最优位置，gbest表示种群历史最优位置。每一次迭代中粒子通过跟踪这两个极值来更新自己。假设有M个粒子在D维搜索空间中以一定的速度飞行。每一个粒子的位置在t时刻的位置可以表示成D维向量，同样该粒子的速度也是一个D维粒子在t+1时刻的位置通过式(4)和式(5)更新获得：

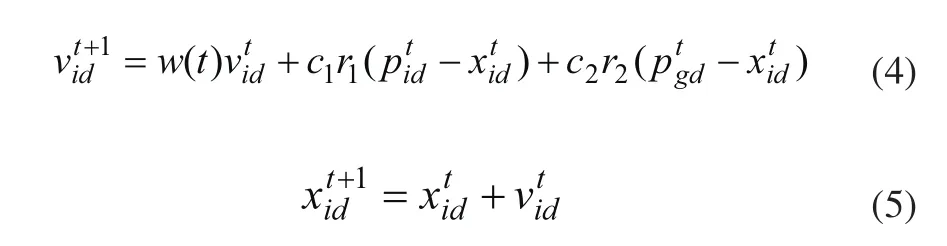
式(4)中，c1，c2为学习因子，通常取[0,4]之间的随机数作为其值。r1和r2为均匀分布在[0,1]区间上的随机数；t的值为当前迭代的次数；w(t)为惯性权重，是粒子群算法中最重要的参数。文献[10]通过实验证明，采用线性权重递减法能显著提高算法的性能，具体计算公式如式(6)所示：

其中，wmax表示惯性权重最大值，取0.9；wmin表示惯性权重最小值，取0.4；t表示当前迭代次数。

3.2 杂交粒子群算法

基本PSO算法在进化过程中会出现早熟收敛的现象，使所有的粒子聚集在某几个特定位置，导致收敛精度的降低。为了避免此类现象的发生，将遗传算法中的杂交思想引入到PSO算法中[11]。在每次迭代中，根据一定的概率pc选取一定数量的粒子随机地两两交叉，产生同样数目的子代粒子，并用子代粒子代替父代粒子。引入交叉有可能使陷入局部最优的粒子跳出来，能提高种群的全局搜索能力。子代粒子位置可由式(7)得出。

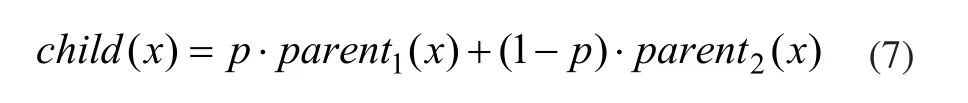
其中，p服从均匀分布且在[0,1]上值，parent1(x)和parent2(x)为亲代粒子位置。子代粒子速度child(v)的计算公式如式(8)所示。

其中，parent1(v)和parent2(v)为亲代粒子速度。当局部最优的两个粒子杂交时，往往可以消除局部最优，从而获得改进的搜索结果。

表3 神经网络测试结果

4 故障诊断仿真过程

4.1 仿真实验

选取NPC三电平逆变器输入电压分别为400V、450V、500V，负载功率分别为40、45、50kW情况下的故障数据，作为样本共计9组数据，取其中8组数据作为神经网络测试样本，剩下1组（输入电压450V、负载功率45kW）作为测试数据。粒子个数设为N=40，惯性权重w(t)采用线性递减的策略，wmax=0.9，迭代至最大次数时的惯性权重wmin=0.4，学习因子c1=c2=2，交叉概率pc采用自适应调整，取值范围为0.75～0.95，最大迭代次数设为tmax=200，误差收敛精度设为0.001，输出编码为1～7。选取网络学习样本的误差作为适应度函数，误差式如(9)所示。

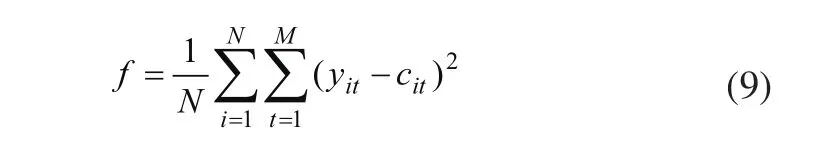
式(9)中，N为训练样本总数，M为BP网络输出神经元的个数，yit为节点的理想输出，cit为节点的实际输出。

4.2 诊断结果

把测试数据输入到经过杂交粒子群优化后的神经网络中进行验证，输出结果如表3所示。从表3可以看到，对神经网络的实际输出进行四舍五入后，与网络的期望输出（故障编码）一致，正确率为100%，误差非常小。由此可见本文提出的方法是切实可行的。

为了进一步地验证该算法在逆变器功率管故障诊断上的准确性，构造3组相同结构的BP神经网络，分别用BP神经网络、基本PSO-BP神经网络及本文采用的杂交PSO-BP神经网络对样本进行训练。图9为分别用三种诊断方法的系统误差变化图。从图9可以看出，在前期的迭代中，基本粒子群算法优化的BP神经网络和杂交粒子群算法优化的BP神经网络在NPC逆变器功率管开路故障诊断的误差收敛的过程中速度都比单一BP神经网络有了明显提高。但基本粒子群优化的BP神经网络在迭代收敛过程中存在长时间的误差停顿现象，而杂交粒子群BP神经网络模型在第76次迭代时就达到了相应的误差条件，说明杂交粒子群算法在NPC三电平逆变器开路故障诊断效果方面优于其他两种算法。

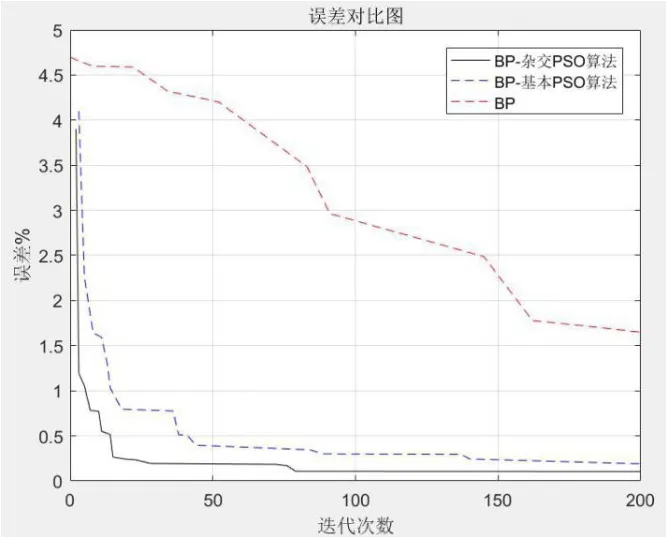
图9 误差-迭代次数变化曲线

5 结论

1）本文提出了一种基于杂交粒子群算法优化BP神经网络的NPC三电平逆变器故障诊断模型。对所有故障进行编码建立故障特征表，能够同时诊断单管开路故障与双管开路故障，精准定位到具体的故障功率管。

2）针对BP神经网络和基本粒子群算法在故障诊断时易误诊和陷入局部最小的缺陷，本文采用杂交粒子群算法优化BP神经网络，避免陷入局部最小，对故障准确识别，有效地避免了误诊断。