公交线网下公交车跳站停靠设置方法研究

李 磊

（重庆交通大学交通运输学院，重庆 400074）

关键字：公交规划；通行能力；跳站停靠；层次分析法

1 研究背景

热门公交站点公交排队与大量乘客等候公交的现象普遍存在，导致乘客与公共汽车的需求矛盾加剧。此外，公交车排队进站过程中，车辆在站台泊车范围不明，乘客无法确定公交车停靠位置，随公交车移动，影响他人乘车；公交车进出站时，极易与当前道路行驶机动车发生冲突，使得公交进出站和乘客乘车效率大大降低，延长乘客出行时间，降低道路通行效率。本文考虑采用跳站停靠的方式来避免列车化现象的产生，对重复系数大，通行能力不能满足需求的公交线路进行简化，提高公交运行效率。

2 研究现状

目前，部分公交站点处交通拥堵严重，公交车运行效率下降。这是因为高峰期间的公交流量超过了站点的服务能力，传统公交运行方法无法满足不断增长的公交停靠需求。而公交跳站停靠策略能够减少部分交通站点的停靠车辆数，同时提升公交运行效率。早在20世纪，在欧美等发达国家的大城市中就已开始采用公交跳站运行策略，我国部分特大城市也开始研究这一策略，其中，吉林大学的孙锋等人通过分析跳站运行对乘客出行时间的影响，建立乘客总出行时间最小的公交跳站运行方法。但在实际运用中，由于缺少实验成果，实际运行效果不佳，出现公交站点利用率低、乘客换乘难等问题，公交服务水平没有显著提高。

3 跳站停靠的设置基础

（1） 一次完整的公交出行要经历四个阶段：①到达公交站点的时间；②乘客等待公交的时间；③公交载客运行时间；④最终抵达目的地的时间。

（2） 路网中只存在公交车和小汽车。

（3） 乘客随机分布在站点周围，且乘客上下车不受其他干扰因素的影响。

（4） 某公交路线在站点i实行跳站停靠后，所有受跳站停靠影响的乘客可以在重复站点换乘其他公交线路来到达目的地。

4 跳站停靠的需求模型

（1） 查询所有待调整线路的站点，并将位于地图上最左端的站点定义为1，然后依次将站点定义为1到n；

（2） 针对所有线路，构建n阶的矩阵，对该矩阵中的元素xij（i，j∈n且i≠j） 定义如下：

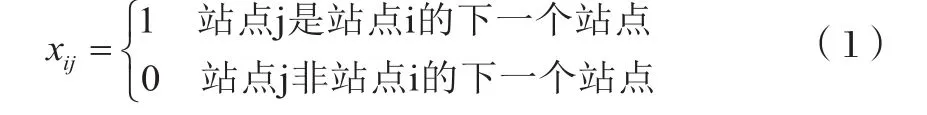
定义该矩阵对角线上的元素xii均为0，由此得到每一条公交线路所对应的矩阵；

（3） 将步骤二得到的任意两个矩阵A和B进行点乘，得到一个新的n阶矩阵Y，则有：

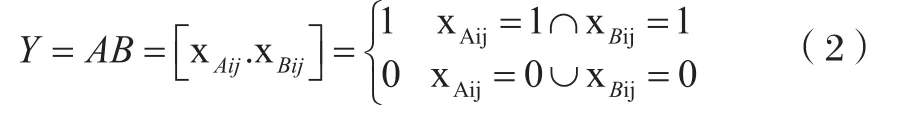
即Yij=1则站点i与站点j为公交线路A和B上的重复站点，反之则不是。

（4） 对所有点乘得到的矩阵进行分析，由站点数字推导出可以设置跳站停靠的站点，以及与之对应的公交路线。

5 跳站停靠的优化模型

5.1 跳站停靠的站点选择

对可以设置跳站停靠的站点进行公交运行分析，将公交线路重复系数大，通行能力不能满足需求的站点作为跳站停靠的优选目标。

5.2 跳站停靠的线路优化模型

（1） 确定一个目标层，将各影响因素 （本方案为各客运线路小时客流量、汽车班数、站点停靠时间） 作为指标层，根据实际调查情况给出各影响因素对于目标层的影响程度，将途径重复站点的线路依次罗列到方案层，并根据实际情况给出每条线路对于指标层各因素的影响程度。

（2） 根据步骤一可以得到n+1个比较矩阵，求解指标层对目标层比较矩阵和方案层对指标层比较矩阵的特征值以及特征向量的求解，并进行一致性验证，然后将特征向量合并得到方案层对指标层的权重矩阵，最后将权重矩阵相乘，则可得到方案层对目标层的权重，而可以从方案层中选出目标线路。

5.3 优化模型的求解

根据实地调查的数据资料构建出指标层对目标层的判断矩阵以及方案层对指标层各指标的判断矩阵B1、B2、B3，然后对待选择的公交站点数据进行分析，将指标层客流量、汽车班次及停靠时间之间两两比较得到三个指标之间的重要程度，从而得到三个指标的判断矩阵A，再将各条线路的客流量、汽车班次以及停靠时间进行汇总整理，则可得相关指标的数据表格，数据内容为：

通过关联矩阵，得到方案层各线路对于各指标的影响程度矩阵B。在此基础之上，通过matlab编程，从而求解出各判断矩阵最大特征值所对应的特征向量，即指标层对目标层的权向量w1，方案层对各指标的权向量w2、w3…wm。现令矩阵将矩阵C和矩阵D相乘即可得到方案层中各方案对于目标层的影响程度wa。通过权向量可得某站点具体是哪条公交线路对该站点的影响最小，则为优化路线。

6 实例分析

本文以重庆市301、313、475三条公交线路为样本，采用上述模型进行分析。由于篇幅问题，涉及的公交站点仅考虑了该三条线路的通过站点。

6.1 跳站停靠的站点选择

根据实际调查，并统计筛选三条公交线路站点，得到一共40个不同的站点，即n=40。根据这40个站点在重庆市内的具体位置，对这40个站点进行赋值，则每一条公交线路都可用一个40阶的矩阵来表示，其中301线路对应矩阵A，313线路对应矩阵B，475线路对应矩阵C。

采用公式 （2），线路A和线路B的点矩阵为YAB，其中YAB（1，2） =1等13个元素的值都为1，即这13个元素所代表的公交站点为301与313这两条线路的重复站点。对这13个元素进行分析，得到不同的数字一共有16个，即共有16个重复站点。

进行比对，得到301和313这两条线路的具体重复站点为磁器街，中兴路等16个站。同理，矩阵YAB点乘矩阵C得到矩阵YABC，求得线路A，B，C的重复站点为四公里，五公里，六公里，七公里。

6.2 跳站停靠的线路选择

将六公里作为跳站停靠线路优化中的目标层，选择301路、313路、475路公交作为方案层。通过数据分析，影响程度大小依次为客流量，汽车班数，站点停靠时间从而可以得到这三个指标的判断矩阵A：

根据相关线路的具体数据可以得到方案层中三条公交线路对于指标层的矩阵B1，B2，B3。指标层对目标层的权向量w1，方案层对各指标的权向量w2、w3、w4。令矩阵C=w1，矩阵，则有：

最终，将矩阵C和矩阵D相乘即可得到方案层中各方案对于目标层的影响程度，本文通过对程序的运行后得到最终的权向量为：

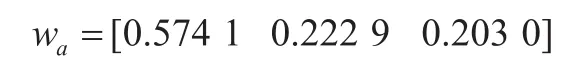
通过该权向量可以得出，在六公里站点301路公交车的影响程度最大，313路影响程度次之，475路公交车影响程度最小，故应该对475路公交进行跳站运行。

6.3 vissim现状仿真分析

采用vissim对该路段的现状及方案进行模拟，同时输出两个主要的评价指标——排队时间和通过数据检测点的瞬时速度，评价指标见表1。

表1 跳站运行前后的运行状态对比

通过仿真前后的运行数据进行对比可以发现：采用跳站停靠后的公交线路的总排队时间减少了51.90%，运行速度提高了23.21%。

7 结语

本文在分析公交跳站停靠的运行策略和公交路网中公交站点运行情况的基础上，建立公交车跳站停靠的优化模型，对城市高峰期拥堵频发的公交线路进行优化。利用vissim对路段优化前后分析可得，在高峰时期设置公交跳站停靠，可以有效地减少公交站点的车流交织，提高站点及其关联路段的通行效率，提升公交线网服务水平，降低城市道路拥挤程度。