基于空心板梁桥的钢波纹板—混凝土拱加固体系简化计算方法研究

赵 洁,袁良东,宋福春

(1.郑州市交通规划勘察设计研究院 郑州市 450000; 2.沈阳建筑大学 交通工程学院 沈阳市 110168)

1 工程概况

车家小三号桥位于京哈高速公路盘锦段K568+040处，建成于1999年。该桥分为左右幅，桥梁全长18m，跨径布置为1×10m，桥面净宽2×15m，该桥上部结构为预应力混凝土空心板，采用桩基础，交角为117°。

近年来，因高速公路交通量不断增长，重载和超载车辆日益增多，该桥现已出现了严重的病害。尤其在我国东北存在多年冻土地区的桥涵工程中，由于桥涵下冻土的上限变化沿桥涵轴线呈现“拱”的形式，故在冻土融化时，若发生融沉现象，则在桥涵的进出口处会产生比路中相对较大的沉降变形；同样当融土冻结时若发生冻胀，则桥涵的进出口处的冻胀翘起变形也比路中大。这样，在桥涵的两端，会相应地产生一定的变形(位移)，同时在涵身产生一定的拉、压应力。由于受资金和气候等条件的限制，这些低等级的桥梁不可能全部拆除重建，只能投资较少的资金进行加固。采用钢波纹板-混凝土拱的结构形式进行加固是一种简单合理且经济快捷的方法[1]。从此意义上讲，在多年冻土地区应用钢波纹板结构桥涵，发挥其优良的变形能力和钢材抗拉性能及抗疲劳性能较好的特点，对预防或彻底解决桥涵因融沉和冻胀而导致破坏较为有效[2]。

2 钢波纹板—混凝土组合加固结构桥梁分析简化

2.1 钢波纹板截面特性换算方法

钢波纹板结构为几何正交异性结构[3-4]，进行相关的三维实体计算和有限元建模分析的时候要考虑其结构特殊性和复杂性。对此，把几何正交异性的三维钢波纹结构简化成三维平板结构，确定误差范围，然后把三维平板结构，进一步简化成二维平面结构，这样在对三维钢波纹板实体结构进行计算和分析时提供了很大的方便[5]。

对以钢波纹板为对象简化为二维结构进行研究，取一个波长的截面进行分析，建立坐标系，其中x轴通过波纹中性轴截面，y轴为垂直x轴向上。

图1 钢波纹板截面特性计算图

通过计算得：

惯性矩：

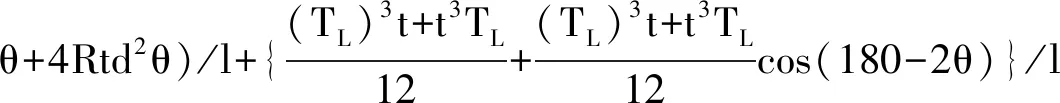
(1)

面积：

A=[4(R+t/2)θ+2TL]t/l

(2)

截面模量：

(3)

回转半径：

(4)

式中：L—波长；

h—波高；

TL—直线段长度；

R—波峰波谷半径；

θ—圆曲线段弧角度(弧度)；

d—圆心偏离X轴距离；

t—板厚。

表1 简化计算值与规范对比

由表1可知，应用上述公式计算值与规范值对比误差在可控范围内，故可以通过该公式来简化钢波纹板截面系数的计算，为后续的分析研究提供基础[5]。

2.2 钢板波纹板拱向平板拱的转化分析

用ANSYS分析三维钢波纹板受混凝土压力，考虑钢波纹板截面受力情况。建立简单模型，采用钢波纹板拱截面形式。以波形380×140×5mm建立直径6m的钢波纹板拱进行受力分析。钢波纹板采用she1193壳单元，在此分析时不考虑混凝土填料本构模型，只考虑钢波纹板受力情况，考虑重力作用下钢波纹板截面应力，如表2所示。

表2 钢波纹板截面应力

将上述计算值汇成图如图2所示：

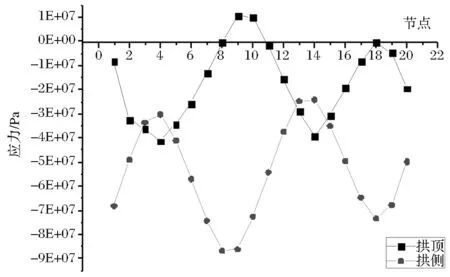
图2 钢波纹管截面应力图

由图2钢波纹板拱截面应力分析可知，钢波纹板中性轴位置对应于平均应力，而波峰与波谷分别对应于最大和最小应力。由材料力学知识推知钢波纹板中性轴截面所受为轴力，而波峰与波谷处最大和最小应力是由于弯矩引起的[6]。

如材料力学中的公式一样：

(5)

由此计算得出拱顶截面：

N=83kN

拱侧截面：

N=260kN

式中：σ2—壳单元最大应力与截面平均应力的差值。

2.3 空间实体模型向平面模型的简化分析

由式(5)计算得知三维钢波纹板管受力时截面受力可以用材料力学平截面假定来分析，由此可以将三维模型简化为二维模型，这将大大简化以后建模和分析。

同样采用上述规格的钢波纹板建立跨径6m的钢波纹形拱，钢波纹板采用beam3模拟，混凝土采用solid95单元模拟。各材料参数与三维模型采用一致，对钢波纹板结构梁单元进行等效尺寸转换：

B·H=A

(6)

B·H3=12Ix

(7)

建立模型求得计算结果与三维模型结果进行对比，见表3。

从对比数据中可以看出，弯矩的吻合较好，仅是轴力存在些许不同，误差不超过9%。因此，可以用平面模型代替钢波纹板三维模型。

表3 三维与二维钢波纹板模拟计算结果对比

3 钢波纹板—混凝土拱加固的实用计算方法理论

3.1 组合截面拱简化模型分析

以前，对各类拱桥进行简化计算时，把拱看作是承受拱上全部荷载的承重结构，同时把拱上结构当作传递荷载至拱上的传力构件。由于忽略考虑拱上结构与拱的联合承载的相互作用能力，计算出来的结果与实际情况往往有很大的出入。

就钢波纹板—混凝土组合拱桥来说，拱上混凝土结构与钢波纹板拱联合形成复杂的超静定受力体系[48]，目前的结构受力计算非常困难。钢波纹板拱上浇注混凝土，所以可视为钢波纹板—混凝土组合结构，对于钢—混组合拱桥简化计算的处理方法：当计算主拱时，按照拱顶混凝土厚度考虑联合作用，计算结果偏安全；当计算拱上结构时，按联合作用考虑，计算结果偏安全。

3.2 钢波纹板—混凝土拱加固实用计算方法

对于钢波纹板—混凝土组合拱结构，采用有限元软件ANSYS对其进行受力分析，图3为钢波纹板—混凝土加固桥梁断面主压应力图，从图中可以看到，拱上混凝土以受压为主，受力区域集中分布在拱顶混凝土高度的拱形区间，钢波纹板与拱上混凝土形成一个近似的拱形联合受力结构，拱上混凝土压力值在靠近拱脚时逐渐减小。

图3 钢波纹板—混凝土加固桥梁断面主压应力图

图4 断面应力迹线图

从图4的主应力迹线中也可以看出，压应力主要沿着钢波纹拱轴线方向传播，在拱脚区域发生一定扩散，拱肩区域受力较小，在混凝土区域形成一个自然的受力拱肋。

根据以上的相关理论和计算分析结果以及加固结构的断面主压应力图和断面应力迹线图可以将钢波纹板—混凝土拱加固结构进行结构简化计算研究分析。整体简化思路如下：

首先，对钢波纹板拱等效成平板拱。根据钢波纹板的具体规格尺寸和截面特性可以计算出钢波纹板等效平板厚度，计算见式(1)～式(7)。钢波纹板拱等效钢板拱的截面，如图5所示。

图5 钢波纹板拱等效钢板拱

其次，对钢波纹板拱上填筑混凝土材料进行等效简化。由于钢波纹板上浇注混凝土之后，混凝土和钢波纹板形成一个整体，协同工作，共同受力，同时混凝土生成一定强度之后为刚性体，我们可以把填筑在钢波纹板拱之上的混凝土结构等效简化为等截面拱圈结构，其截面厚度取其拱顶厚度，其余混凝土可以根据自重等效恒载施加在拱圈上，保证等效结构的自重荷载不变。拱上填筑混凝土结构的简化如图6所示。

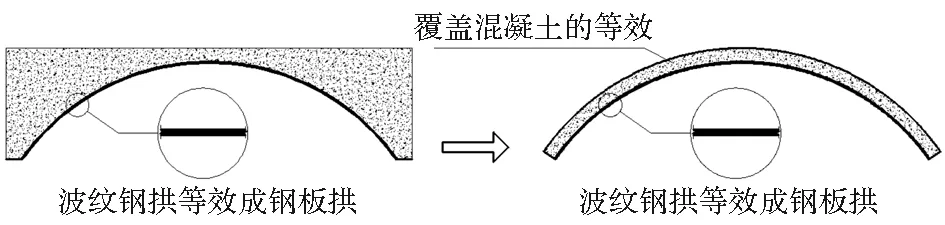
图6 拱上混凝土结构截面的简化

对钢波纹板—混凝土加固结构进行等效简化之后，加固结构的截面即简化为如图7所示。

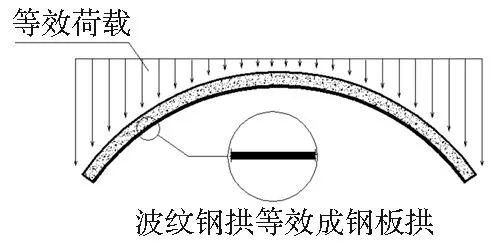
图7 加固结构的截面简化图

钢波纹板—混凝土加固结构的等效简化是在满足材料截面特性误差范围内以及结构合理的受力形式的前提下进行的，简化后的形式既方便我们对结构进行有限元模型的建立和分析，避免了建立复杂的三维空间实体模型，同时在三维计算和建模分析的时候因结构的特殊复杂性带来了困难和不便，甚至导致结果的不准确性，对复杂的三维空间实体模型的分析对计算的要求也很高，给研究也带来了不便。等效简化后的计算模型，不仅可以使一般水平的研究人员对此类结构进行有限元分析，而且节省了建模时间和分析计算时间，提高了工作效率。

4 简化计算流程和方法

在此基础上通过材料力学公式把三维结构的钢波纹板拱—混凝土加固桥梁简化为二维平面结构。由此钢波纹板—混凝土拱组合可以总结为以下计算流程图(见图8)。根据简化流程图可以更清晰地了解简化思路，为我们此类加固方法提供了参考，也方便相关的研究人员更快捷、高效地进行研究。

图8 简化计算流程图

5 结语

本文主要依据有限元结构软件来分析钢波纹板混凝土拱桥梁加固体系的结构受力、变形等特性。结合钢波纹板的力学特性和变形特性在加固工程中具有较强的适应能力，对钢波纹板的桥梁结构分析简化，在三维计算和建模分析的时候，由于结构的特殊性，这里把三维空间结构简化成二维平面结构，通过理论公式的计算和建立有限元模型分析的计算对比之后，发现误差很小，满足简化要求，进而推出钢波纹板—混凝土组合拱桥的简化计算流程和方法，为我们以后进行此类结构的计算分析提供了参考。