制造企业零部件随机库存控制模型

马庆祥

(1.合肥工业大学管理学院，安徽合肥 230091；2.安徽城市管理职业学院，安徽合肥 230011)

0 引言

科学的控制原材料库存量，以规避存货不足带来的缺货损失以及库存过多所带来的库存成本压力已成为制造企业必须要解决的问题。库存在制造业物流成本中占有相当高的比例，以专业设备制造业为例，2012—2017年该行业存货指标一直呈增加趋势[1]。存货增长的一个主要原因是原材料库存控制不合理造成的。因此，科学合理的控制库存，可以有效降低生产成本，保证生产经营的高速运转，提高资金使用效率。

在随机型库存问题研究方面，何春敏等[2]根据存贮理论设计了关键零部件库存控制方法，并为满足实际需求和降低库存成本费用，结合实际计算核心零部件的库存控制值。戢守峰等[3]研究由零售商发起订货，但零售商不能控制订货间隔期的多周期库存优化问题，给出一种预期利润函数，该函数适合补货间隔期为一般分布的情况。施文武等[4]在采用(s，Q)(库存降至s时，生产量为Q)策略建立生产/库存模型的基础上，设计一种可以有效减少库存平均费用的生产控制方法。王雨等[5]运用Flexsim软件设计了仓储作业流程模型，为企业优化生产流程，合理控制库存提供理论依据。朱锦红[6]在前人研究的基础上构建基于供需双随机型的三级库存控制模型，对降低库存成本具有一定现实意义。赵靓[7]根据IT制造企业备件特点，构建了考虑库存成本与服务水平均衡的备件库存控制模型。万娜娜等[8]从3个不同库存策略角度对随机需求环境下供应链库存系统的可靠性进行研究，并验证了其有效性。张春晓等[9]在不确定随机变量的条件下引入机会理论，建立周期性订货优化模型，并给出当利润实现最大化时订货策略的最优解析解。陈素芬等[10]把有限期内企业的利润最大化作为目标函数，并假设随机变化的原材料采购价格服从布朗运动，分析了企业原料采购的最优库存策略。王安[11]通过库存量与服务质量的关系，拟合出安全库存与服务水平之间的关系。构建了库存成本优化模型。吴燕燕等[12]通过灵敏度分析认为在生产库存控制决策中应首先减小过程参数的变化区间与截尾方式上下限。刘峥等[13]研究双渠道供应链联合库存实施策略，认为通过库存共享，可以协调2个渠道的库存水平，减少缺货风险，达到降低供应链成本的目的。Xiao等[14]研究不确定装配能力的按订单装配问题，提出利润最大化模型，以此控制最佳库存。Chao等[15]研究具有随机供应能力的定期审查库存系统的补货和定价的联合优化问题。高聪等[16]根据产品之间的单向可替代性，提出一种满足用户需求的订货点确定策略，并为此采用模拟退火算法求解各产品的最高库存量。郭彩芬等[17]应用极大代数理论分析串行生产线离散事件动态系统的多周期生产过程，建立生产与库存控制模型，得出理想的在制品库存量应接近初始库存量的结论。邱若臻等[18]研究在需求概率不确定的情况下多周期库存鲁棒优化模型，通过对比发现该模型在库存订货策略方面具有很好的鲁棒性。林勇等[19]在比较研究单周期库存模型的基础上,构建了多周期的制造业通用件库存模型。吴鹏等[20]通过动态规划方法，研究需求未定条件下半成品存货的多周期生产决策问题，给出最优的多周期生产策略并分析了各参数对最优策略可能产生的影响。

以上研究策略或模型大多适用于所进货物用于直接销售的经营性企业，而对于制造企业来讲，进货是为了满足本企业的生产需要，并不直接用于销售。本文将从最小期望库存成本角度出发研究制造企业多周期随机库存的控制问题，以期得到理想的库存量，从而更好地解决制造业生产中需求的不确定性，减少零部件缺货损失。

1 离散型需求的多周期随机库存模型

在制造业日常库存系统中，每个生产周期对零部件的需求是一个不确定的随机变量，这个随机变量可能是离散的，也可能是连续的。首先建立需求为离散型随机变量的库存模型，然后在此基础上讨论需求为连续型随机变量的库存模型。

制造业零部件多周期随机型库存的需求是长期的、重复的，需要不断的补足存货，但由于需求是随机的，从订货至到货的时间间隔比较长，若在库存较充足的条件下就开始订货会增加存储、货物成本等方面的费用[21-22]。反之，若零部件库存不足，则会影响企业正常生产，进而影响企业交货周期，给企业造成很大的经济损失[23]。所以，适合采用的最优的库存策略就是找出最佳的库存量，从而在保障企业正常生产的情况下使得系统期望库存总成本最小。

1.1 模型基本假设

假定每个周期的费用结构是相同的，库存总成本由订购成本、货物成本、存储成本和缺货成本4部分构成[24]。可以选择其中某一个周期当做考察目标，各项费用假设如下。

1)订购成本e。e主要包含订单处理成本费、催货跟踪费、运输费和装卸费等,各周期e不变。

2)每个周期的最大库存R。期初库存为I,期初订购量为Q，R=I+Q。

3)货物单位成本h。h主要指货物本身的成本，包括货物的价格及搬运中的损耗费等。

4)单位货物的存储成本a。a主要包括货物的保管费、损耗费等。

5)单位货物的缺货成本b。缺货成本通常远大于货物自身的成本。

1.2 建立模型

借助文献[25]的研究方法，假定本期零部件需求为X，那么当X≤R时，库存零部件能够满足企业生产需要，剩余的零部件(R-X)留作下期的期初库存，忽略已使用部分的存储费用，本周期的存储费用为a(R-X)。

当X≤R时，系统的期望库存成本

(1)

当X>R时，生产需求没有完全得到满足，缺货量为(X-R)，缺货带来的损失为b(X-R)。相应的期望库存成本

(2)

由式(1)(2)得系统的总期望库存成本

(3)

由于X为离散随机变量，可以通过求解minE[C(R)]确定最佳库存量Rop。

1.3 模型的扩展分析

实际应用中要使系统总期望库存成本最小，必须确定Rop，可以通过边际分析法求解不等式确定Rop。

1)求解不等式E[C(R)]≤E[C(R+1)]

由式(3)得

(4)

则：

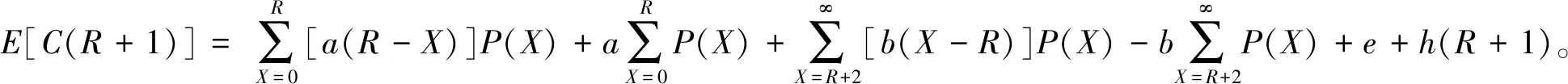
(5)

因为E[C(R)]≤E[C(R+1)]，由式(4)(5)得

(6)

由于

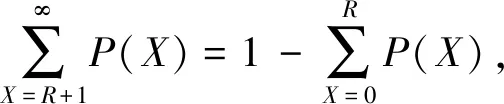
(7)

将式(7)带入式(6)并整理得

(8)

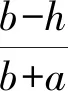
2)解不等式E[C(R)]≤E[C(R-1)]

同理解得

(9)

由式(8)(9)得：

(10)

即Rop由式(10)确定。

2 连续型需求的多周期随机库存模型

2.1 确定模型

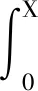
(11)

(12)

2.2 确定Rop

因为需求是随机的，并且有初期库存I，则在确定R后，是否订货取决于I，若不订货则可节省订购费用e。

当I≤R，且I非常靠近R时，订货可能是不经济的。若订购，该期总期望库存成本如式(11)所示。

若不订购，该期总期望库存成本

(13)

因为E[C(I)]≤E[C(R)]，由式(11)(13)得

(14)

由式(14)可知，存在不止一个I，使得不等式成立，应选择最小的I作为订货时Rop。因此不订货是经济合理的。

所以该模型的库存控制方法是每期初检查I，若I

3 实证分析

某制造企业生产某产品，2017年6月至2017年7月对零部件A的日需求量统计如表1所示，1 d统计1次，故表1中“时间”为零部件A的日需求量出现在相应区间的时间。

表1 某制造企业6、7月份A零部件日需求量统计

已知该零部件的进价为23元/件，缺货费用为60元/件,存储费用为3 元/件·d，每次定购费为300元，拟确定零部件A的最佳库存控制方案。

利用式(14)确定零部件A的最佳库存控制方案，需要确定其密度函数。在未知日需求量服从何种理论分布的情况下，对其分布提出假设，然后用已有数据通过皮尔逊检验来证实总体是否服从假设的分布。其步骤为：

1) 提出原假设H0，即日需求量总体的分布函数为F(Xmin，Xmax)；

2) 根据表1可知：Xmin=60，Xmax=300，日需求量总体的取值范围为6个互不重叠的小区间，即：(60，100]、(100，140]、(140，180]、(180，220]、(220，260]、(260，300)。实测频数(统计时间，1 d统计1次)n1～n6分别为10、8、10、12、10、11，则实际统计总频数n=n1+n2+n3+n4+n5+n6=61。

3)根据假设的总体分布理论，算出日需求量落入第i区间的概率pi，则npi为落入第i区间的样本值的理论频数。表1中共有6个区间，假设为均匀分布，那么日需求量落入区间(60,100]的概率p1=1/6，区间(60,100]的理论频数为np1=61/6。依次类推，可以计算日需求量落入另外5个区间的理论频数。

>name<-c("60-100","100-140","140-180","180-220","220-260","260-300")

>frequency<-c(10,8,10,12,10,11)

>data<-data frame(zone=name, frequency)

>set seed(1234)

>chisq.test(data[, 21], y=NULL, correct=TRUE,

+ p=rep(1/length (data[,41]), length (data[,41])), rescale. p=FALSE,

+ simulate p value= FALSE, B= 2000),

Chi-squared test for given probabilities

data: data[,2]

x-squared =0.868 85, df=5, p-value=0.972 4。

可知P=0.972 4，大于给定的显著水平α=0.05，差异不显著而接受原假设，即日需求量服从F(60，300)的均匀分布，由式(12)得零部件A的密度函数

(15)

以1 d为周期，已知：h=23元/件，b=60元/件，a=3元/件·d，e=300元/次。

由式(14)得：

解得：69.7≤I≤507.5。

则取Rop=70，即每天检查库存量I，若I<70件，则订货，订货量为(142-I)，否则不订货。

4 结语

本文参照制造业现有成本构成，改进传统模型中与现实生产脱节的弊端,综合考虑订购成本、货物成本、存储成本和缺货成本等因素,所建模型较传统模型更贴近实际。通过条件假设，首先给出需求为离散型的制造业多周期随机库存控制模型，然后用数学方法证明了确定最佳库存量时累计概率的存在并推导出计算公式。在此基础上，进一步给出需求为连续型的制造业多周期随机库存控制模型。通过分析，两种情况下的模型均能在保证系统总期望成本最低的情况下确定最佳库存量。