智能汽车横向运动控制关键技术及现状

李爱娟，葛庆英，赵晓丽，邱绪云，王希波，陈政宏

(山东交通学院汽车工程学院，山东济南 250357)

0 引言

智能汽车[1]作为智能交通[2](intelligent transportation systems，ITS)的重要组成部分，其良好的发展可以有效降低交通事故，节约能源，因此诸多企业、高校纷纷投入大量资源进行研发。智能汽车主要由环境感知、决策与规划、运动控制3部分组成[3]，运动控制部分是其中的关键技术之一。智能汽车的运动控制分为横向控制和纵向控制。横向控制是指通过对自动转向系统的控制，实现智能汽车的路径跟踪；纵向控制是指通过对油门和制动的协调，实现对期望车速的精确跟随[4]。本文主要研究智能汽车横向运动控制中的关键控制技术。

1 智能汽车运动控制概况

运动控制广泛涉及到各个领域，包括工业[5]、医疗[6-7]等。智能汽车运动控制仅仅是被细分的一个运用领域[8]。本文所涉及的横向运动控制最初是由美国通用汽车公司和美国无线电公司在20世纪50年代末合作开发的[9]，目的是为解决自动化公路系统 (automated highway system，AHS) 车辆自动驾驶问题[10]。从那时起，智能汽车运动控制问题便得到了学者们的广泛研究，从经典控制理论、现代控制理论，到如今的智能控制理论[11-12]研究，逐渐转型升级，衍生出众多的适应时代需求的控制方法。模糊控制方法不需要建立精确的数学模型，鲁棒性强，但需要不断切换输出比例因子，易引起算法震荡甚至收敛困难[13]；神经网络控制方法拥有较强的处理非线性系统的能力，鲁棒性强，但控制算法较为复杂，应用范围受到限制[14]；鲁棒控制方法稳定性好，但需要对系统进行精确建模，对于非线性系统来说，实现精确建模往往较为困难；最优控制方法是在一定的限制条件下实施控制，对于参数时变以及高度非线性系统，难以达到较好的控制效果[15]。因此，伴随着研究的深入，能够满足智能汽车行驶环境复杂、时滞性、高度非线性的衍生运动控制方法逐渐被人们所接受，主要包括基于比例-积分-微分(proportion integration differentiation，PID)控制的运动控制方法[16]、基于模型预测的运动控制方法[17]和基于滑模变结构的运动控制方法[18]。

2 智能汽车横向运动控制的关键技术

本文在部分已有研究的基础上，将智能汽车的横向运动控制方法主要分为基于PID控制、模型预测控制和滑模变结构控制，如图1所示。

图1横向运动控制方法分类

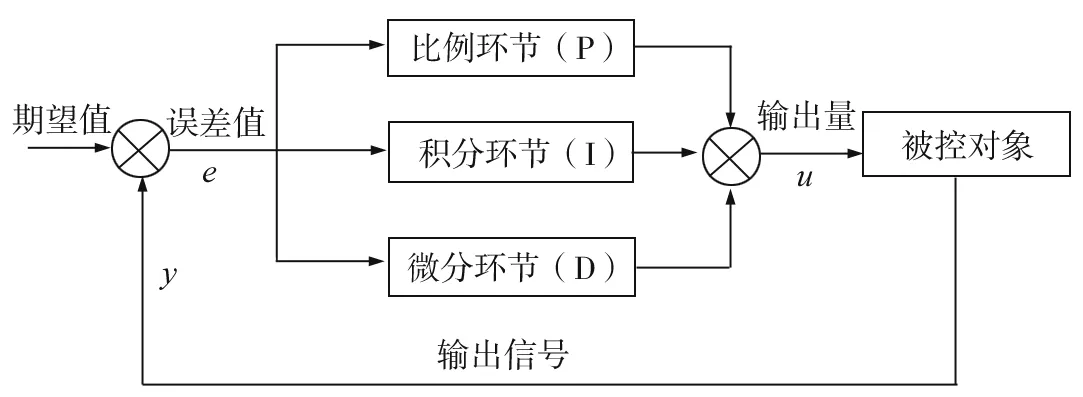
图2 PID反馈控制原理框图

2.1 PID控制

PID控制器以其结构简单、易实现且能达到较好的控制效果，广泛应用于控制领域[19]。经典的PID控制由比例单元P、积分单元I和微分单元D组成，其反馈控制原理如图2所示。

如图2所示，首先对输入误差e进行比例、积分、微分运算，运算后的叠加结果u作为输出量以控制被控对象，同时被控对象融合当时状态输出反馈信号y，再次与期望值进行比较，得到的误差e再次进行比例、积分、微分调节，如此循环进行，直至达到控制效果[20]。对于PID控制器的设计，关键问题是关于比例控制参数kP、积分控制参数kI以及微分控制参数kD的整定，参数超调、参数能否快速响应以及是否消除静态误差，都取决于参数的整定问题[21]。传统的参数整定依赖于经验试凑法，对于高度非线性、强耦合的智能汽车来说，不能很好的满足其控制要求，因此，近年来PID结合模糊控制、神经网络控制以及人工智能等对参数整定进行优化，对智能汽车进行融合控制，可以进一步提升控制效果。

文献[22]采用模糊PID控制算法，通过模糊规则进行推理决策，实现PID参数的实时优化，相较于传统的PID控制，具有响应时间短、适应性强、控制精度高的优点；为解决传统PID控制在智能汽车控制中的稳态误差和敏感性较大等问题，文献[23-24]引入BP神经网络与PID进行联合控制，最大特点是可以自动识别数学模型、进行自我训练和学习，能够使控制参数在线自我调节，可以有效提高控制精度；智能车辆运动控制的最终结果是达到与驾驶员的控制行为高度一致，文献[25]提出基于人工智能技术的PID控制，将粒子群算法、蚁群算法、萤火虫算法等进行比较，仿真结果表明采用独立分析仪来确定PID参数，能够将车辆的输出调整到期望的轨迹，保持车辆的稳定性，与PID控制器相比，具有速度快、精度高的优点。

传统PID控制方式算法简单，可对智能汽车进行横向控制，但因控制参数往往通过试凑法获得，难以实现对智能汽车的最优控制[26]。将传统PID控制与模糊控制、BP神经网络以及人工智能的有效结合进行控制，可以有效提高控制性能，实现控制参数的实时优化，但基于PID的控制器设计依然难以有效的应用于多变量、多约束的优化系统。

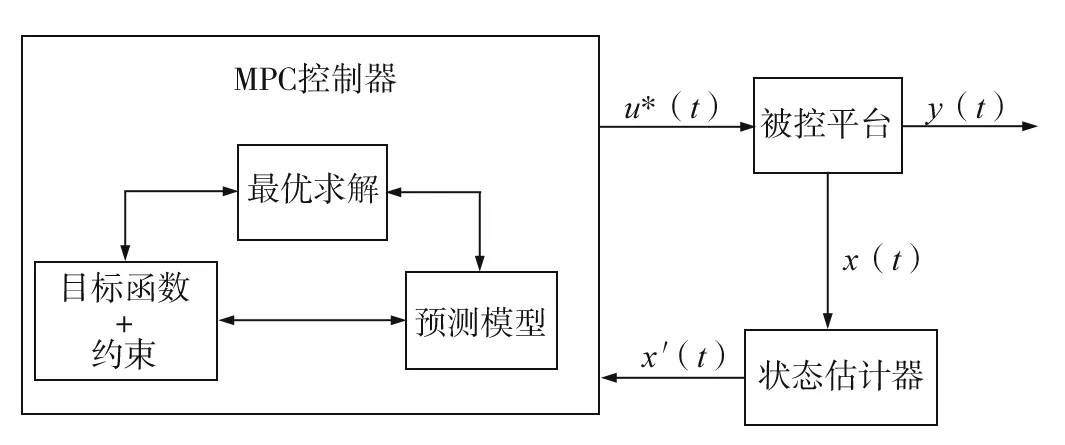
图3 模型预测控制原理框图

2.2 模型预测控制

模型预测控制(model predictive control,MPC)起源于工业界，意在解决PID控制不易解决的多变量、多约束的优化问题[27]，具有处理线性和非线性模型，同时观察系统约束和考虑未来行为的能力[28]，近年来广泛用于智能汽车路径跟踪控制[29]。MPC主要由预测模型、滚动优化和反馈调整3部分组成，基于MPC的控制器原理如图3所示。

如图3所示，MPC控制器结合预测模型、目标函数和约束条件进行最优化求解，得到当时的最优控制序列u*(t)，并将其输入被控平台，被控平台按照当前的控制量输出y(t)对被控对象进行控制，然后将当前的状态量观测值x(t)输入状态估计器，状态估计器对于无法通过传感器观测到或者观测成本过高的状态量进行估计，将估计的状态量x′(t)输入MPC控制器，再次进行最优化求解，如此循环，构成闭环反馈控制系统[30]。依据预测模型的形式将MPC分为线性时变模型预测控制和非线性模型预测控制两种。

2.2.1 线性时变模型预测控制

线性时变模型预测控制方法以线性时变模型作为预测模型，该方法的最大优点是计算较为简单，实时性好，因此广泛应用于智能汽车的运动控制中[31]。对于行驶在有限区域的智能汽车，通常以车辆运动学建模、以前轮转角为控制变量，结合车辆动力学、执行机构和状态约束进行控制器的设计[32]。为提高预测模型的匹配程度，文献[33]采用递归最小二乘法进行实时在线系统辨识，结果表明,此方法实时性较好，可以生成最优转向角控制指令进行车道保持控制；为提高车辆控制的稳定性，文献[34]以基于曲率的一阶和二阶空间导数的最小化为控制目标，同时添加约束以避免偏离参考路径，保证了良好的路径跟踪精度；文献[35]在传统的MPC控制基础上，将执行机构的动力学纳入控制设计，并应用二次规划方法计算转向的最优轨迹，实现转向系统的精确平滑跟踪。

2.2.2 非线性模型预测控制

严格意义上来说，线性系统是非线性系统近似或者是简化后的结果[36]。对于高速行驶的智能汽车以及非结构化的道路(一般是指城市非主干道、乡村街道等结构化程度较低的道路)行驶环境，往往需要更精准的控制以及实时避障[37]，此时需要运用非线性模型预测控制进行控制器的设计，即加入更多的控制变量、采用先进的优化方法以及考虑运动学和动力学进行综合建模等。文献[38]在面对高速和非结构化道路环境下，同时优化参考速度和转向角，控制车辆高速避障，其优点是不需要事先了解环境和参考轨迹；文献[39]在以车速和转向角为控制变量的基础上引入遗传算法进行优化求解，结果证明所用方法能够准确、稳定地控制车辆行驶；为充分描述车辆运动学和动力学特性，文献[40]建立了运动学和动力学综合模型，可以使车辆稳定行驶，不足之处是计算量较大，可以运用相应的数值优化工具和优化算法有效减少计算量[41]。

总之，模型预测控制可以进行实时滚动优化，在线处理建模误差和干扰约束等问题，有效应用于高速以及非结构化道路环境，可以使行驶车辆有较好的控制稳定性，与此同时在线冗余量较大，可以考虑加入终端约束和状态约束[42]、最小化横向偏差和方向误差[43]以及采用微分进化算法[44]等，进一步减小在线计算量，缩短反应时间。

2.3 滑模控制

滑模控制 (sliding mode control，SMC)本质是一类特殊的非线性变结构控制，是由前苏联学者Utkin等在20世纪50年代提出的[45]。其非线性表现为控制的不连续性，控制原理为根据系统所期望的动态特性来设计系统的切换超平面，通过滑动模态控制器使系统状态从超平面之外向切换超平面收束；系统一旦到达切换超平面，控制作用将保证系统沿切换超平面到达系统原点，这一沿切换超平面向原点滑动的过程称为滑模控制[46]。SMC对非线性系统以及未知干扰具有较强的鲁棒性，究其原因是系统存在抖振现象[47]。单一的SMC往往不能满足智能汽车控制的要求[48]，改进基于滑模变结构的运动控制方法成为研究重点，主要方向有融合比例-微分 (proportion differentiation，PD) 控制、自适应模糊控制[49]以及神经网络控制[50]的控制方法。文献[51]针对高速自主导航智能汽车的鲁棒性、精度高、时间限制严格的特点，设计了一种基于结构和运动模型的滑模控制器，通过对线速度和角速度的控制，能实现智能车辆对任意轨迹的跟踪,控制效果较好[52]。

2.3.1 结合PD的滑模控制

结合PD的滑模控制基本思想是利用PD控制的简单易设计和滑模控制的鲁棒性，提出一种新的控制律，避免两者固有的缺点，以此进行控制器的设计。文献[53]针对多自由度直线平移机器人系统的轨迹跟踪控制问题，提出滑模控制PD，其中PD控制用于控制被控系统，而SMC用于补偿干扰和不确定性，可以有效减少跟踪误差，仿真结果验证了该算法的有效性和鲁棒性。同样，文献[54]结合PD和SMC提供了一种无模型非线性反馈机制，并与stand PD和SMC控制方式进行比较，证明了所提出的混合控制方法的有效性。文献[55]在前者的基础上，采用自适应PD滑模控制算法，并基于李雅普诺夫理论进行稳定性分析，进一步提高了控制器的适应性和鲁棒性。

2.3.2 自适应模糊滑模控制

针对智能汽车高度非线性、强耦合、参数不确定性以及难以建立精确模型的特点，基于滑模控制并通过自适应模糊算法对不确定性和未知干扰进行补偿的控制策略可以有效降低跟踪误差，具有良好的控制性能。为获得车辆相对于参考路径的精确位置信息，文献[56]采用基于视觉算法的自适应滑模控制策略，用来抵消非线性和不确定性的影响，并基于李雅普诺夫理论进行稳定性分析，证明其具有良好的控制性能。文献[57]设计了基于输入输出线性化的自适应模糊滑模控制系统，仿真结果表明：即使外界因素发生变化，系统仍能准确的跟踪期望路径，横向偏差和方向偏差都快速趋于零，并且能有效降低车辆抖振，此方法车辆低速时控制效果较好。而对于高速行驶的智能汽车，文献[58]提出一种新的自适应模糊滑移控制系统，利用模糊系统对未知的非线性函数进行逼近，可以有效处理复杂的动态环境，并基于李雅普诺夫理论验证其稳定性。基于自适应模糊滑模的控制策略可以达到较好的控制效果[59]，所以此控制策略也被广泛应用于自主水下机器人的控制[60-62]。

2.3.3 结合神经网络的自适应滑模控制

针对智能汽车对于参数变化和未知的外部干扰，滑模控制方法可以获得满意的跟踪性能，但在基于模型的控制器设计中，由于模型简化过程中产生误差，使得控制质量下降，因此引入神经网络对各种不确定扰动进行建模和估计，以此进行动态控制器的设计。文献[63-64]采用一种具有双曲正切函数的特殊结构的自适应神经网络，仿真证明此控制器在保持滑模系统稳定性和鲁棒性的同时，对系统运行中所产生的故障具有良好的抑制能力；文献[65]采用模糊神经网络系统逼近传统的滑模控制律，并引入监控补偿器来消除近似误差，可以达到较好的控制效果；文献[66-67]采用具有逼近任意非线性函数的径向基函数(radial basis function,RBF)神经网络，能够有效提高系统对多角度旋转的全向车辆的控制性能，保证闭环系统的全局渐近稳定性，进一步提升控制效果；对于具有多角度旋转的全向车辆，文献[68]提出一种基于人工神经网络的自适应滑模控制，对各种不确定性扰动进行建模和估计，建立全向车辆的运动学和动力学模型，并与经典的SMC和PID控制进行比较，进一步验证其有效性和鲁棒性。

总之，基于滑模变结构的控制器设计，其自身特点导致控制系统存在抖振现象，同时又不能将抖振完全消除，正是因为抖振现象的存在，使得控制系统在参数不稳定以及外界干扰等条件下，仍然具有较强的鲁棒性和自适应性。在此基础上结合PD控制、模糊控制以及自适应神经网络控制，使得智能汽车在复杂行驶环境下，可以较大限度的提高系统的鲁棒性和控制精度。

3 发展趋势

对智能汽车的运动控制来说，如何将其他控制领域的先进技术，与自身的运动状态相互结合，切实优化自身的运动控制效果，将是未来研究的方向，智能汽车横向运动控制方式的发展趋势为：

1)深入、多层次地研究现有的控制方式。考虑更加全面的优化控制策略，秉承存在即合理的优化思想，针对复杂的道路环境，从控制结构、算法等多策略方面思考优化方向，设计更完善的控制方式，例如考虑混合模型多约束的优化控制策略等。

2)积极结合其它领域的优势控制方法。通过自然界中生物的一些特有的生理结构和生活习性，深入探讨能够运用到智能汽车的仿生运动控制方式，例如是否可以模仿蛇的生理结构开发一种适合智能车辆转弯工况的稳定控制器等。

3)与外部信息有效结合进行控制。基于智能网联、大数据等一些先进技术，打造基于互联网的车路协同控制，依据实时提供的道路信息及其他因素，对智能汽车进行有效合理控制。

4)高度人工智能控制。现阶段的人工智能依托庞大的数据库，以进行相应领域所谓的“人工智能”，相信随着未来科技的发展，拥有自身独立思想的人工智能汽车终将出现，实现真正意义上的无人驾驶。

4 结论

智能汽车属于高维的复杂系统，难以建立精确的数学模型，同时还面临着非线性、时滞性以及不确定性的干扰因素，难以实现最优控制。传统PID运动控制方式与神经网络和模糊控制的融合，弥补了PID参数整定的困扰；模型预测控制基于有效的模型和数值优化工具，广泛应用于多变量、多约束的系统状态，且控制效果良好；滑模控制结合PD、神经网络等，可以达到更好的车辆控制精度，提高运动控制的鲁棒性。实践证明，将一种或几种控制方式有效结合，可以进一步提高智能汽车的控制性能，为早日实现汽车的无人驾驶打下坚实的基础。