泥质岩土石料填筑体变形特性试验研究

文琪鑫， 邓荣贵， 孙 怡， 李凯甜

(西南交通大学土木工程学院， 四川成都 610031)

1 泥质岩土石料的使用与研究

高速公路、机场跑道及工厂等越来越多地在山区出现，挖填平场是不可避免的，由于运输条件限制，许多填方采用就近取材原则，以大块石作为填料进行土石方填筑，填筑体的变形是一项工程的控制因素，其变形规律对优化设计和工程安全至关重要。

土石填料的典型特点是颗粒级配和均匀性差，采用强夯工艺进行土石料填筑是目前较为主流的做法，块石填方地基强夯处理需注意填料粒径及级配、回填方法、分层厚度和检测与评价等施工要点[1]，填筑高度和压实度是影响沉降量的主要因素[2]，采取增大石料的含量与提高压实度方法可以减小土石混合料自重应力引起的瞬时压缩变形[3]。有学者提出土石混填路堤强夯加固深度需考虑强夯加固范围内各影响因素并给出了相应计算公式[4]。在进行高填方沉降预测时，通过反演计算模型的材料参数结合数值分析是一种较为准确且有效的办法[5]，也可以采用考虑初始压实度、初始含水率及土石比与所受荷载预测填筑土层强度和沉降量的算法[6-7]。有学者利用数值模拟研究了高填方边坡的沉降，提出了填筑层数对边坡沉降的影响[8]。岩石的流变性与绝大多数岩体工程的失稳和破坏有关，蠕变既是岩石的特性，也是土和碎石混合料的重要特性，是土和碎石混合料能否应用于高填方工程和预估高填方工后剩余沉降量的重要依据[9]。除了对一般土石的研究，也有很多对黄土、膨胀土等特殊土高填方的研究，如考虑地形和压实度因素对黄土高填路堤沉降量影响[10-11]，对膨胀土采用“芯土”及外包土用作路基填筑的方法，与外界水体隔离，有效防止弱膨胀土遇水失稳等各种病害[12]。但对于泥质岩这种也需要作为特殊土对待的岩体，鲜有从固体大颗粒角度，对土石料填筑体在荷载作用下的变形机理研究。本文采用土石料填筑体长期变形模拟试验装置，对某机场泥质岩填筑体进行了变形机理分析，建立了对数数学模型，对泥质岩开挖土石料填筑体变形机理进行了阐述。

2 泥质岩土石料试验概况

2.1 试验设备

本试验目的是研究岩石固体大颗粒填筑体的长期变形。而现有设备主要针对小颗粒，一般工程填筑体土石料原型设计级配的最大粒径可以达到800～1000 mm，考虑尺寸效应，设备大小必须是颗粒平均粒径的3～5倍以上，若将大颗粒缩尺太小，其变形规律可靠性偏低，且无法考虑温度、含水量变化对土石料风化影响，故现有设备无法满足试验需求。

本试验采用自主研制的土石料填筑体长期变形模拟试验装置，该试验系统包括支撑装置、水循环系统和风循环系统，支撑装置上设置有模型箱，支撑装置上固定安装有加载时，延伸至模型箱内、并对模型箱内的土石料填筑体施加竖向载荷的加载装置，加载装置上设置有采集土石料填筑体竖向压缩变形量的采集装置。该设备模型箱的尺寸为72.6 cm×75.6 cm×76 cm(长×宽×高)，可做最大尺寸160 mm，最大加载量油压表读数20 MPa，换算至试样顶面荷载为496 kPa，可以实现填筑体自然加载变形、风化变形、降雨软化变形、蠕变变形及多种因素耦合的综合变形试验等功能。本试验仅使用其自然加载变形功能(图1)，首先将试样用土石料按预想设计置入支撑装置，然后采用加载装置，即模型顶部由三个液压千斤顶依靠反力装置加载，传力路径为千斤顶、U型槽钢、传力板，土石料堆填试样顶面，侧向约束为四块双层1.5 cm厚有机玻璃板(聚甲基丙烯酸甲酯)外套U型槽钢约束，有机玻璃板拉伸强度为50～77 MPa，弯曲强度为90～130 MPa，断裂伸长率为2 %～3 %。随着加载变形试验的进行，读取采集装置数据，并统计试验后颗粒形态及级配参数，发现其规律，达到试验目的。

图1 土石料填筑体长期变形模拟试验装置

2.2 试验设计

由于土石料粒径较大，采用原型尺寸开展相应的室内试验难度较大，故需对原型土石料进行缩尺。本试验采用相似级配法，通常是全料的粒径皆被缩小, 使粗粒含量变小, 细粒含量增大, 导致试样性质发生变化，但此试验采用的是均匀大小颗粒，即均匀级配，故采用相似级配法可以保持颗粒级配几何相似、不均匀系数及曲率系数不变，且其能较好反映工程性质。试验终止标志为试样变形达试样总高的20 %，或试样明显破坏。本试验试样为红层泥质岩，取自四川某在建大型机场工程，岩体颗粒主要集中在140～160 mm之间，采用自由堆填方式，试验模型全貌图如图2。

图2 试样及试验设备

试验步骤如下：

(1)安装双层透明有机玻璃板模型箱。

(2)将拟选尺寸泥质岩大颗粒，随机、逐一轻放至模型箱内，在接近顶部时，选用形态粗糙度类似颗粒进行铺填，整体呈自由堆填。

(3)安装传力装置、加载装置和测量装置。

(4)按每级荷载油压表读数1 MPa加载，即试样顶面荷载为24.8 kPa加载，每级变形稳定后进行下一级加载，至油压表读数19 MPa，终止加载。期间观察颗粒破碎变化，记录加载板位移，即试样变形。

(5)采用筛分法统计试验后岩样颗粒级配特征。

载荷作用位移采用电子千分表测量，共计4个测点(图3)。

图3 位移测点布置

3 填筑土石料特征

3.1 填筑土石料形态特征及颗粒级配特征

本文随机选取20个泥质岩颗粒，利用计算机图像分析软件Image-Pro Plus6.0获取颗粒的轮廓，并用2种定量方法测量这些颗粒的IPP圆度和轮廓分维数，再结合鲍尔斯目标对比法对土石料颗粒形态特征进行说明(图4)。

图4 部分试验初始填料颗粒

每个颗粒形态各异，具有很强随机性。颗粒岩性均均匀，岩石表面自然状态下岩体手捻粉末感，湿岩手捻摸有滑腻感，当水分较大时，较为粘手，没有颗粒感存在。岩石主要吸收绿光和少量蓝光、黄绿光，其颜色主要表现为综红色，不透明；其为分子键矿物构成，对光的吸收程度小，反光能力较弱，光泽即弱，属土状光泽。测得IPP圆度和轮廓分维数如图5、图6所示。

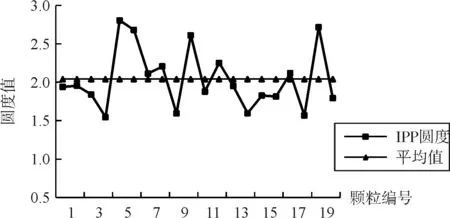
图5 IPP圆度

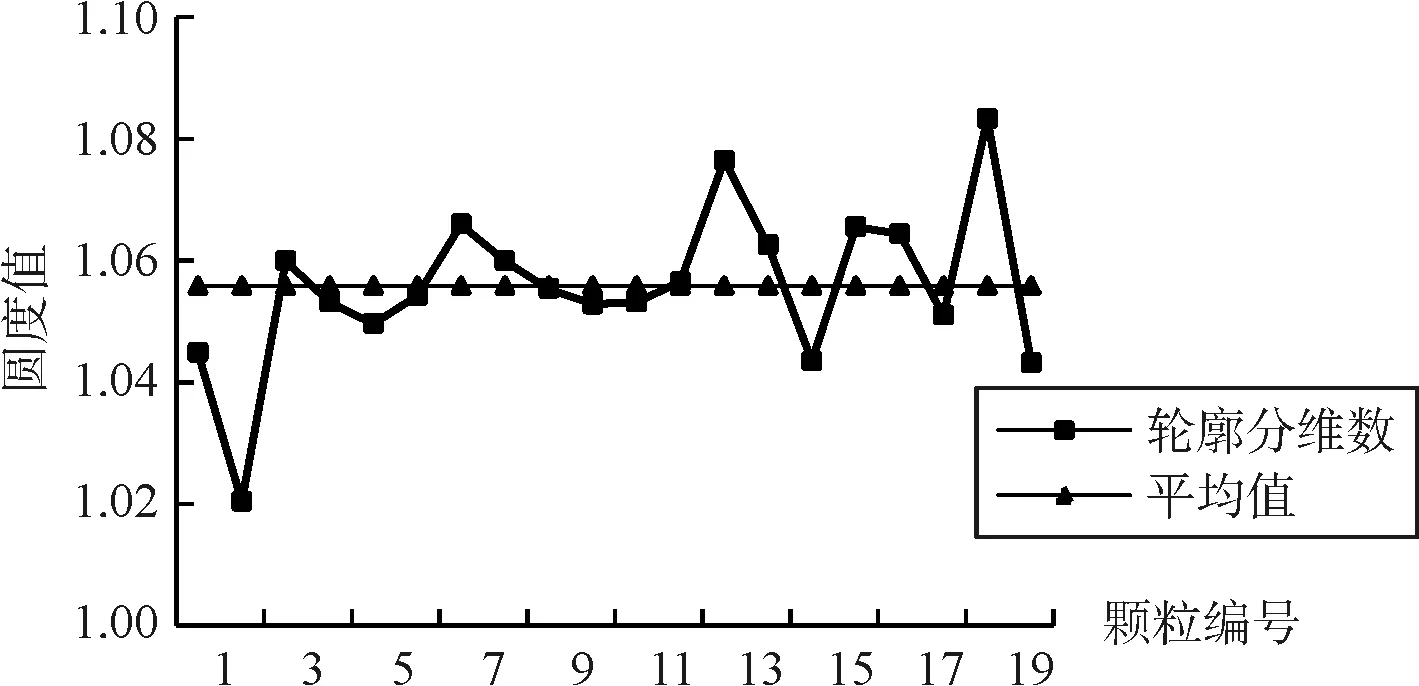
图6 轮廓分维数

IPP圆度是以偏离正圆面积来计算圆度，岩石圆度一般大于1，其值越大越不圆。此岩样颗粒IPP圆度均大于1.5，平均值为2.04。轮廓分维数是用一较小标尺长度去量测轮廓周长，直到标尺长度接近颗粒最小直径时停止，并经过系统计算所得到，其值越大颗粒轮廓越不规则。此岩样颗粒轮廓分维数均大于1.02，平均值为1.057。结合目估对比法，根据鲍尔斯圆度标准，所有颗粒均属于尖棱角状。

试验所用粒径主要集中在140～160 mm之间，质量在2.900～4.100 kg之间，为均匀级配，平均粒径为146 mm，颗粒级配曲线如图7。

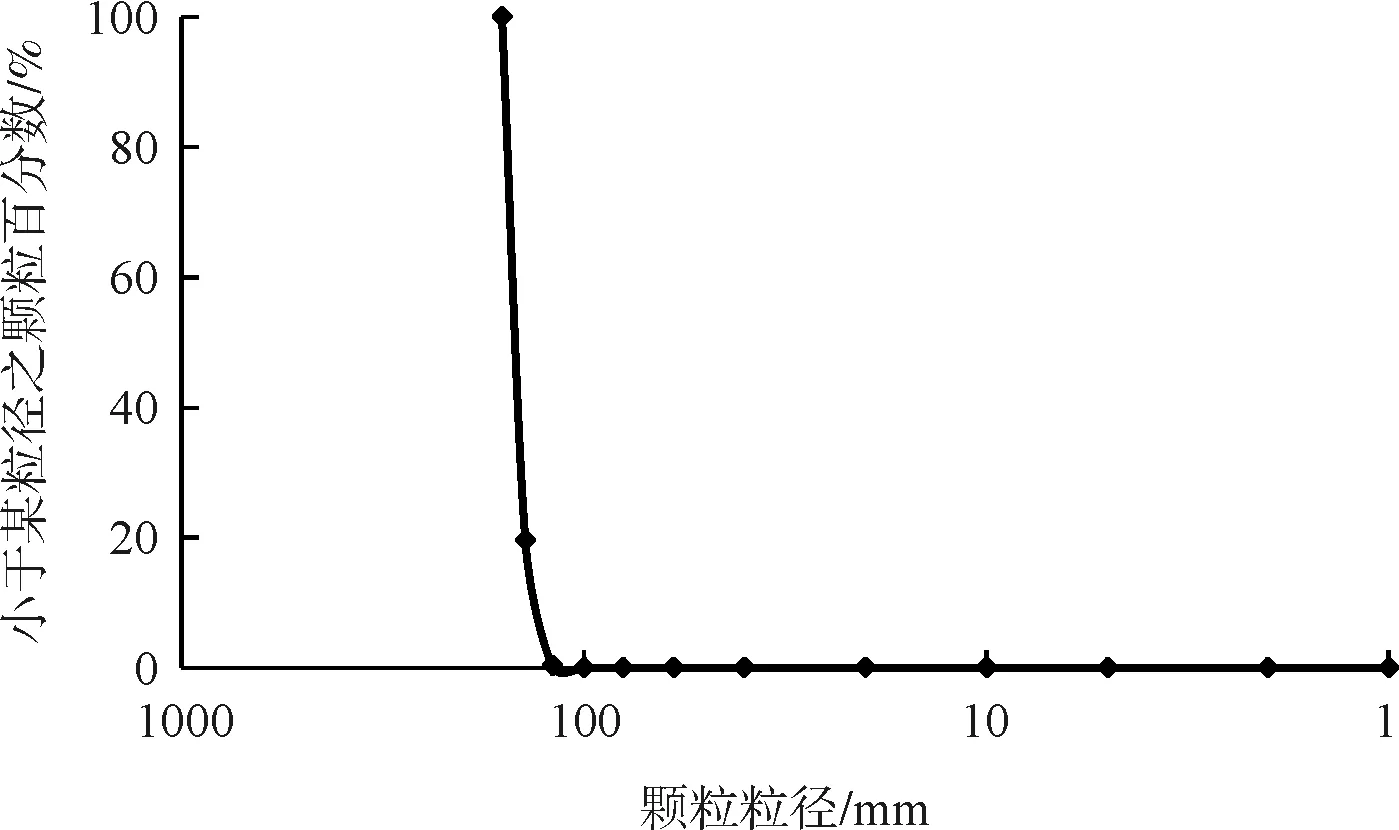
图7 初始颗粒级配曲线

3.2 填筑土石料物理力学特性

填料用泥质岩初始含水量为2 %，天然重度为2.38 g/cm3。采用机械钻孔加工7个标准岩样，即直径50 mm，高100 mm的圆柱体型，分3个进行单轴加载试验，4个进行三轴加载试验。

3.2.1 单轴加载试验

三个岩样岩性基本相同，最大荷载平均值为7.60 kN，应力为3.87 MPa；最大位移平均值为1.5188 mm，应变为0.0152。三者在达到峰值前后均经历一段波动，但峰值附近波动变形较小，这与岩石原处地应力条件及风化程度有一定关系。三者在达到峰值后应力下降，表现出一定的脆性特征。岩样单轴加载参数如表1所示，变形曲线如图8所示。

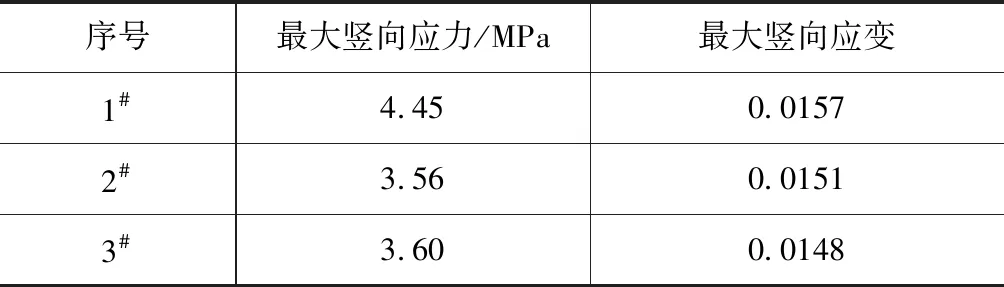
表1 单轴加载参数

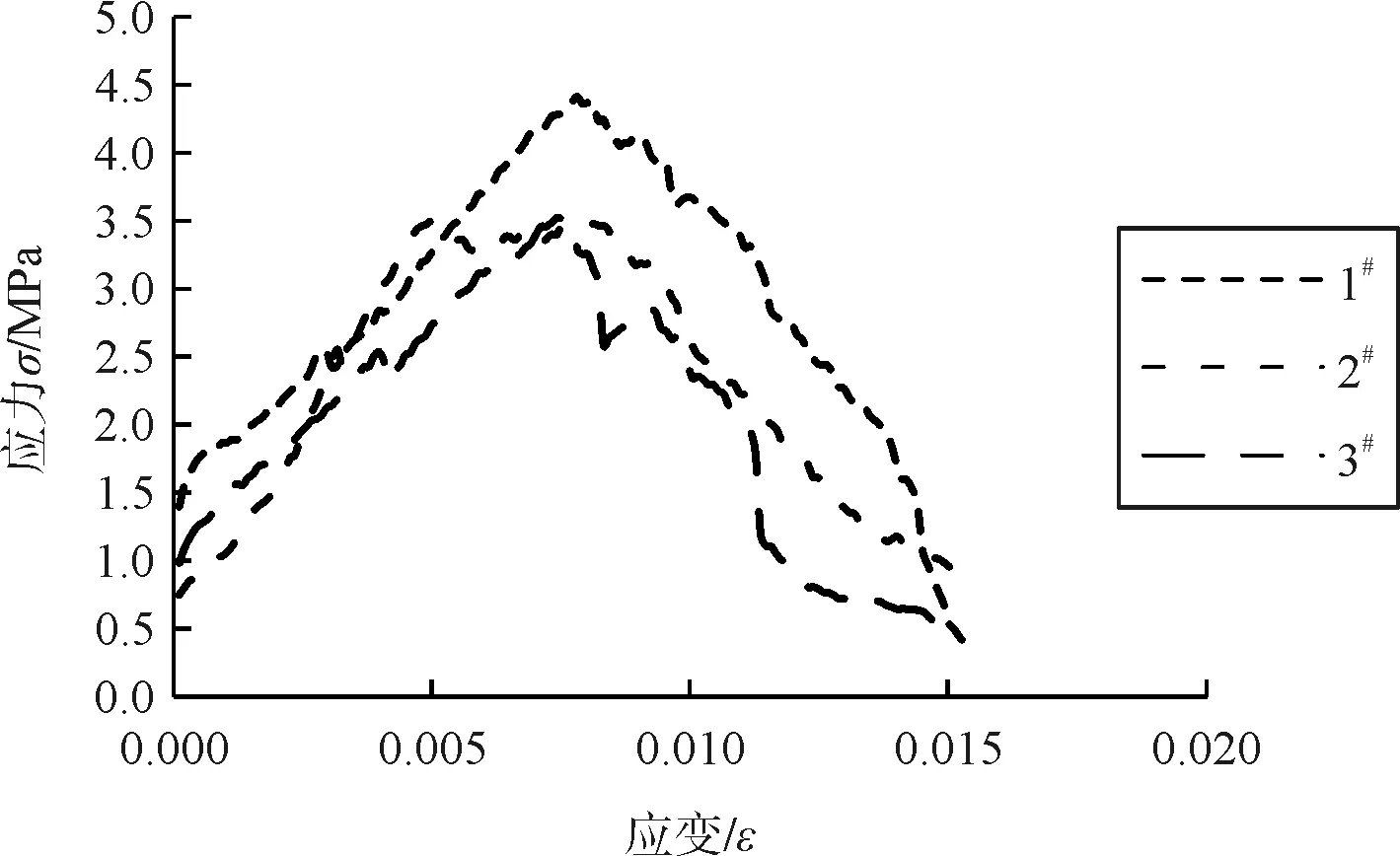
图8 单轴应力-应变曲线

3.2.2 三轴加载试验

三轴试验是常规情况下的，即σ1>σ2=σ3，施加的围压分别为是1 MPa、2 MPa、3 MPa和4 MPa。加载试验实施方案如下：首先以0.5 MPa/s 的速度施加轴压和围压至静水压力值(即预设围压值)，并保持15 s不变，此过程采用应力控制模式；然后保持围压不变，继续以0.5 MPa/s 的速度施加轴压，直至岩样破坏，此过程采用位移控制模式。岩样三轴加载参数如表2所示，三轴变形曲线如图9所示。

表2 三轴加载参数

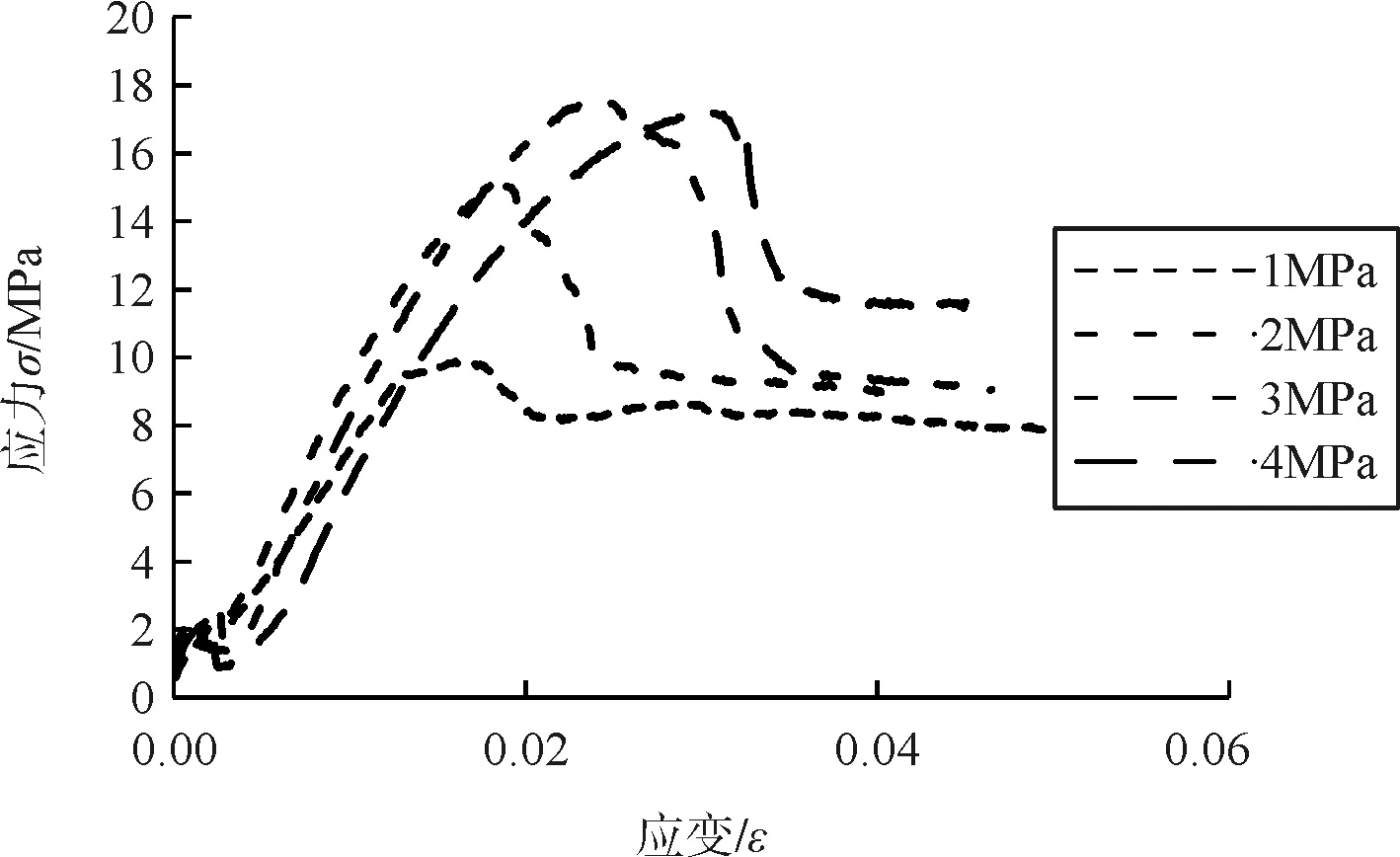
图9 三轴应力-应变曲线

根据三个单轴试验岩样不难看出，岩石岩性基本相近，故三轴试验结果图像差异主要由围压控制。在处于1 MPa的相对低围压状态下时，当竖向荷载达到5.10 MPa时，荷载将不再上升基本保持不变，直到竖向位移达到限值；围压2 MPa时，其峰值竖向荷载有明显上升，增加为8.05 MPa，为围压2 MPa时的1.5倍，峰值后下降至5.10 MPa附近直至破坏；围压3 MPa、4 MPa时，其峰值荷载相近，为9.17 MPa，较围压2 MPa时无明显上升，围压3 MPa岩样破坏时荷载与围压1 MPa、2 MPa相近，围压 4 MPa破坏荷载为前三种的1.2倍。

四者图像均在达到峰值后迅速下降一段，然后趋于稳定，说明在围压作用下先表现脆性，再表现出延性。单轴和三轴变形曲线中均未体现出压密阶段，可以认为岩石自然状态下较为密实。

4 填筑体土石料变形特征及分析

4.1 填筑体变形特性及其分析

土石料填筑体在荷载小于120 kPa时，变形较为迅速；120 kPa与240 kPa之间，变形较为缓慢，并伴有岩石破碎声；240 kPa与320 kPa之间变形速率适中；320 kPa与447 kPa之间，变形缓慢，有微弱岩石破碎声，在趋近447 kPa时，变形变化很小，总变形量达到了82.4 mm，大部分颗粒肉眼可见破坏，认为此时填筑体达到了破坏状态，试验终止。

通过对试验过程的观察及数据的整理，可以认为泥质岩土石料填筑体均质颗粒在荷载作用下的变形可分为四个阶段：岩块似弹塑性变形阶段，岩块接触面(点)压裂变形阶段，填筑体块粒空间结构崩溃失稳变形阶段和岩块破碎与空隙闭合挤密变形阶段。整体变形规律可用对数模型进行拟合(图10)，散点图为荷载-变形曲线，光滑对数曲线为拟合曲线，垂直于横轴的点画线为四个变形阶段分界线。

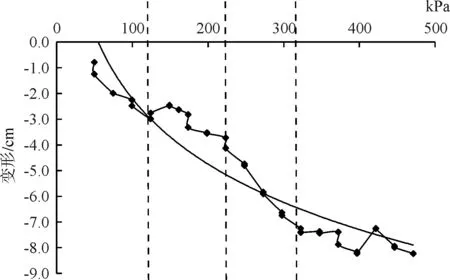
图10 荷载-变形曲线

由拟合曲线可以建立荷载变形数学模型，相关系数为R=0.938，如下：

s=-3.674ln(F)+14.721

(1)

式中：F(kPa)为填筑体顶板荷载，s(cm)为填筑体竖向平均位移。

土石料本构模型常用土体的压缩特性双线性函数模拟，即当平均应力p小于屈服应力时，材料处于弹性变形状态；当其超过屈服应力后，土体颗粒开始破碎，圧缩曲线下弯明显，塑性体积变形持续积累[13]。本文试验为侧限约束单向加载，荷载-变形曲线为对数函数模型，故采用下述指数函数[14]进行理论计算：

(2)

式中：e0为材料的初始孔隙比；hs为固相硬度，是堆石料抵抗能力的一种综合度量，量纲与应力一致；n是无量纲量，由材料级配确定。

堆石料为均匀级配，n取1.204 8，hs取2 004 kPa，初始孔隙比e0=0.481,则据式(2)得e-logp曲线如图11光滑曲线所示。试验所得e-logp曲线如图11带标记线所示。

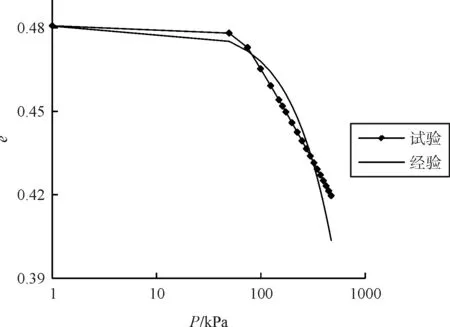
图11 试验和理论得e-logp曲线

试验测点数据主要落在陡倾段，说明本试验所用均匀大颗粒，初期具有很强结构性，在荷载作用下，颗粒接触点首先得到破坏，破碎颗粒填充孔隙，结构发生破坏变形，即从加载初始就进入了颗粒破碎阶段。试验结果曲线和经验曲线较为接近，对于均匀大颗粒堆石料变形计算可采用(1)式，且可直接从颗粒破碎阶段开始考虑。

4.2 填筑体变形后的颗粒特性及其分析

按变形后填筑体总高从上至下分为三层进行颗粒级配统计分析，因颗粒原型尺寸较大，破碎无明显分层，统计按每层厚度约20 cm进行，对于有些颗粒贯穿于上下层，按颗粒尺寸1/2为界，将颗粒归为体积较大部分所处层。分别计算三层及整体的不均匀系数、曲率系数(表3)。

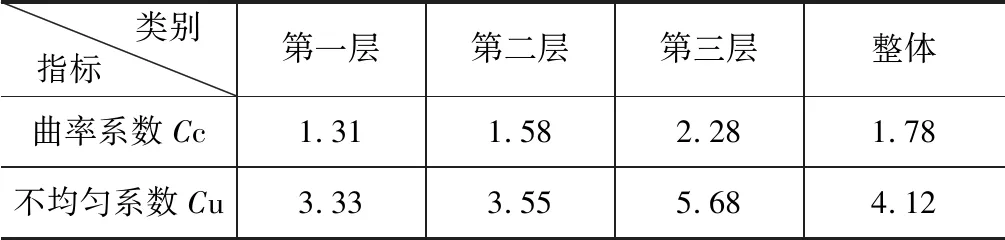
表3 各层及整体级配指标

各层及整体的曲率系数均在1～3之间，第一、二及整体不均匀系数均小于5，第三层不均匀系数大于5，级配指标评价为良好。试验后各层间指标差异不大，各层与整体级配指标差异也不大。如图12，从试验前整体和试验后各层及整体级配曲线可以看出，试验后曲线明显缓与试验前，这是因为随着颗粒破碎形成大量不同粒径小颗粒，填补泥质岩大颗粒之间空隙，且空隙被挤密，填筑体密实度增大；也可以看出试验后从上往下级配逐渐变好，结合试验观察，可以说明在静荷载作用下下层挤密效果良好，此试验第三层密实度较高，可以作为工程填料参考级配。

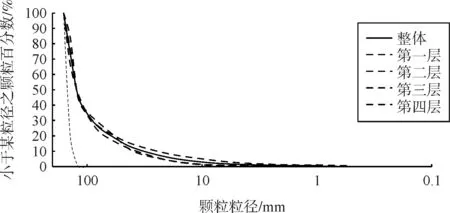
图12 试验前整体和试验后各层及整体级配曲线

5 结论

(1)泥质岩开挖土石料颗粒从IPP圆度和轮廓分维数的定量描述，其平均值分别为2.054、1.057，均大于鲍尔斯目估标准颗粒的尖棱角状对应值，且结合目估对比法定性分析，该颗粒群均为尖棱角状。

(2)填筑体在侧限刚性约束的竖向荷载作用下经历较快，缓慢夹破碎声，中速，缓慢夹破碎声四个不同变形阶段，其可察觉破碎声均发生在变形缓慢阶段，说明填筑体的变形主要受块粒空间结构控制，土石颗粒破坏为辅。

(3)填筑体变形随应力变化近似对数规律，可采用文中数学模型对此类均匀颗粒自由堆填体进行变形预测，变形可分为四个阶段：岩块似弹塑性变形阶段，岩块接触面(点)压裂变形阶段，填筑体块粒空间结构崩溃失稳变形阶段和岩块破碎与空隙闭合挤密变形阶段。在实际工程中应重视堆填体的空间结构布置，以增大第三变形阶段的载荷区间，提高承载力，减少沉降量。

(4)加载完成后观察第三层具有较好挤密效果，且经筛分统计，该层颗粒级配良好，故所得级配参数可用作工程土石 料填筑体参考。

本试验研究仅为初步的，泥质岩土石料颗粒特性与开挖方式的关系，以及不同初始级配对土石料填筑体变形的影响等问题尚需进一步研究。