对流层效应的距离偏差及其改正误差──GNSS导航定位误差之四
刘基余
(武汉大学测绘学院,武汉 430079)
GNSS信号穿过对流层和平流层时,其传播速度将发生变化,传播路径将发生弯曲,该种变化的80%,是源于对流层。因此,常将两者对GNSS信号的影响,叫做对流层效应。研究表明,对于工作频率在15GHz以内的微波而言,对流层将使该种信号的传播路径比几何路径长,所导致的传播路径弯曲较小而略之不计。对流层导致的GNSS信号传播路径增长的距离,叫做超长径距(excess path length)。它是GNSS信号的实际传播路径S与几何路径ρ之差,即,对流层效应导致的GPS信号传播路径偏差为D
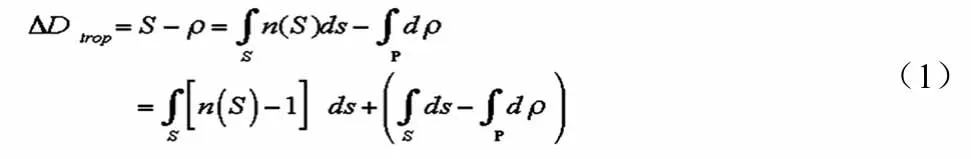
式中,n(S)为对流层的微波折射率。式(1)的第一项,是对流层导致的路径偏差距离,其相应的时间,叫做对流层时延。当GPS卫星在天顶方向运行时,对流层偏差距离为2.3m左右;当GPS卫星在5°高度角运行时,对流层偏差距离约为25m。式(1)中的第二项,是对流层导致的GPS信号传播路径弯曲,其值约为毫米级,而被而略之不计。
对流层偏差距离,常定义为天顶方向上的对流层偏差量ΔDZ与相应卫星高度角ES的映射函数M(ES)之积:

研究表明,90%的对流层偏差距离,是源于大气中干燥气体的影响,称之为对流层偏差距离的干分量,且以ΔDZdry示之,它是大气分子的偏振位移引起的。除此以外的10%的对流层偏差距离,是由大气中水分子的偶极距引起的,称之为对流层偏差距离的湿分量,且以ΔDZwet示之。与干、湿分量相应的映射函数M(ES),也分解成干、湿映射函数,分别记作Mdry(ES)和Mwet(ES)。故有
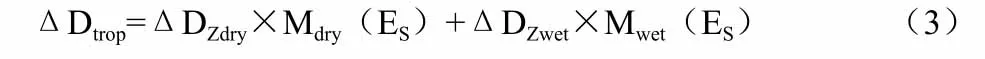
式(3)中的映射函数,常用Chao方程式和Davis方程式。Chao方程式,通过对无线电探空观测的平均折射率剖面而用经验拟合给出的,它与地面测站的气象要素无关,即,Chao映射函数为

式中,脚标n=dry,wet(干、湿分量);且知
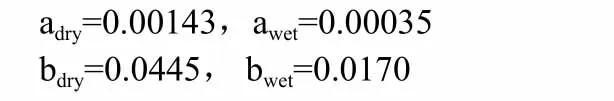
当采用Chao映射函数时,对于5°以上的卫星高度角,该模型误差导致的对流层偏差距离改正误差,占总对流层偏差距离的1%~2%。为了减小Chao映射函数的模型误差,Davis等学者提出了Chao映射函数干分量的修正公式:

式中,

此处,TG,PG,eG分别为地面测站的温度、大气压和水蒸气压;Ht是同温层的高度;α为温度线性递减率,即
式(3)中的ΔDZdry和 ΔDZwet, 可采用加拿大学者J.Saaastamoinen给出的下列公式:

式中,f(B,h)是测站纬度(B)和高程(h)的函数,即,
f(B,h)=1- 0.00266cos2B-0.00028h
从上可见,按式(3)计算对流层偏差距离改正时,首先要选用一定的映射函数,进而按式(6)计算出ΔDZdry和ΔDZwet,才可算得对流层偏差距离改正。为了改进这种算法,美国H. S. Hopfield等学者提出了直接计算对流层偏差距离干、湿分量的下述公式:

上式常称为Hopfield对流层偏差距离改正模型。它的干、湿分量ΔDdry和ΔDwet依下式计算:
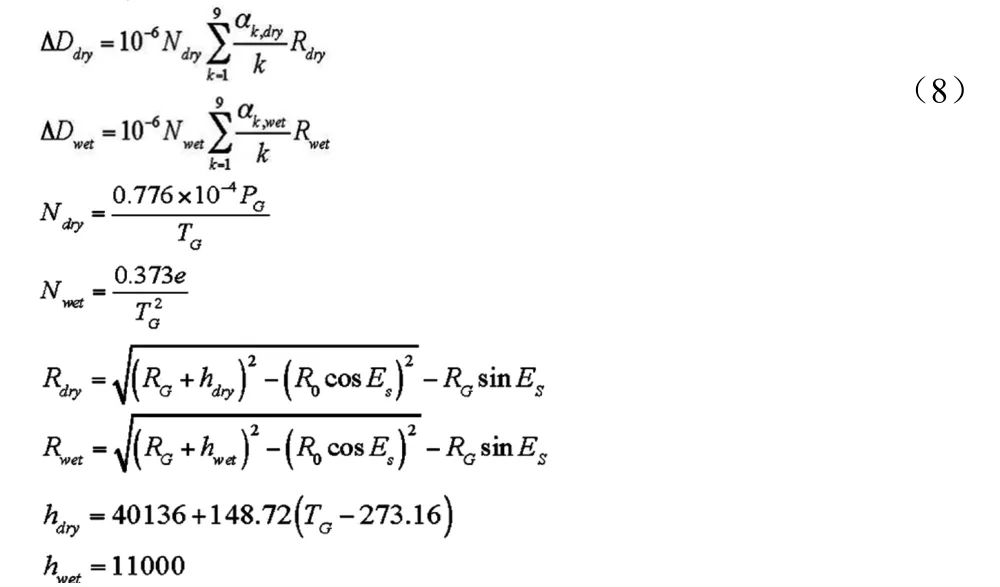
此处的PG、TG、e是测站的大气压力(以毫巴计)、大气温度(以开计)、水蒸气压(以毫巴计);Rdry、Rwet分别为测站到传播路径与干、湿折射指数Ndry、Nwet趋近于零的边界交点的距离(以米计)。式(8)的αk,dry和αk,wet系数;简化成下述形式:

此处,
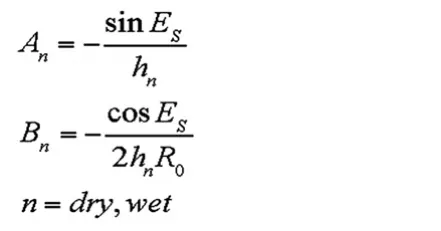
上式中的ES为GPS卫星的高度角;R0是测站的地心向径(以米计)。
在现有Hopfield模型的基础上,我们提出并实践了一种简化计算过程而适用于任一高度的对流层效应偏差改正模型;其基本思想是,对于高程H处的对流层效应的干项和湿项偏差改正(KdH和KwH)用下列积分式:

式中,T0,P0,ew0为已知高程(h0)处的绝对气温(K)、大气压力(mb)和水蒸气压力(mb);hd为对流层外边缘的高度(m),且知,hd=40136+148.72(T-273.16);hw为对流层湿项偏差改正的协议高度(m),即,hw=11000m;T为高程H处的绝对气温,且知

高程H处卫星高度角为E时,其对流层效应偏差距离改正为:
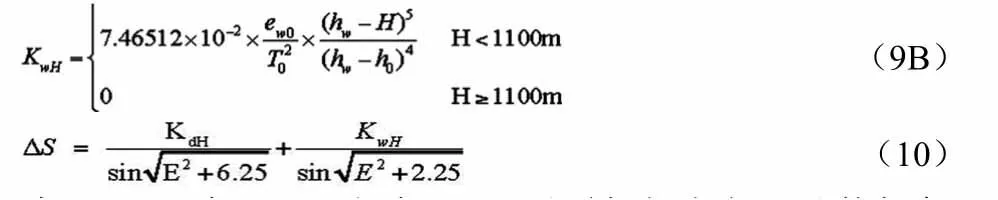
式(9A)、式(9B)和式(10)只需根据方程h0处的气象要素即可计算出高程H处的对流层效应偏差距离改正。若H=h0,由式(9)与Hopfield模型完全相同。
为了验证这种方法的正确性,采用我们的简化模型(方法一)和根据Hopfield模型及其计算方法(方法二),并用同一组气象要素(高程h0=0m,t0=18℃,P0=1013mbar,相对湿度RH=50%)计算了不同高程处天顶方向的对流层效应偏差距离改正,计算结果见表1。由此可见两种方法在0.01mm量级上是完全相同的。

?
从上述可见,对流层效应偏差距离改正误差,主要来自两个方面:其一是对流层效应偏差距离改正的数学模型的不精确性;计算表明,用同一个GPS观测站的气象要素,而按三、四种不同的数学模型计算出的对流层效应偏差距离改正值,对于卫星高度角10°左右的观测成果,其较差大达6cm左右。另一个误差源是气象要素代表性误差;在作对流层效应偏差改正时,依理论而言,应采用沿波径的气象要素(T,P,e)。人们即使采用昂贵的水汽辐射计探测大气的水蒸汽压,而实现对湿分量的改正,其精度也不过厘米级。GPS用户一般无法获取沿GPS信号传播路径的气象要素(T,P,e),而采用由平均海平面处的气象要素按一定数学模型推估处于任一高程处H的GPS测站的气象要素(T,P,e,例如,DIPOP GPS数据处理软件即用该种方法),由此所获取的气象要素与实际值相差较大;称之为气象要素计算误差;即使在GPS测站处实测气象要素,它们也不能代表沿GPS信号传播路径的气象要素,而存在代表性误差。因此,GPS测距的对流层效应偏差距离改正误差,是对流层效应偏差距离改正数学模型误差与气象要素代表性误差之和,其值可能达到亚米级。这再次表明,不能够将GPS测距的“偏差”与“误差”混为一谈!

