引入迷失探索与集群分裂机制的改进鸽群优化算法
尚志刚,王 力, 李蒙蒙, 李志辉
(1.郑州大学 电气工程学院,河南 郑州 450001; 2.郑州大学 产业技术研究院,河南 郑州 450001; 3.河南省脑科学与脑机接口技术重点实验室,河南 郑州 450001)
0 引言
生物种群中单个个体的智能水平往往有限,但整个生物群体却表现出处理复杂问题的能力.群体智能就是受自然生物群体行为的启发而产生的一类重要的人工智能方法.Colorni等从生物进化的机理中受到启发,通过模拟蚂蚁的寻径行为,提出了蚁群优化算法[1],但其收敛时间过长,易陷入局部最优[2];Kennedy等通过观察鸟群觅食行为提出了粒子群优化算法[3](particle swarm optimization,PSO),其收敛速度较快,但易陷入局部最优[4].鸽子具有特殊的归巢能力,它们被认为使用太阳、地球磁场和地标的组合来寻找巢穴.Roberts等认为,鸽子可能在旅程的不同阶段使用不同的导航工具[5],Guilford和他的同事开发了一个数学模型,可以预测鸽子何时从一种导航方式转换到另一种方式.当鸽子开始它们的旅程时,它们可能会更多地依赖类似指南针的工具[6];在旅途中,当它们找到熟悉的地形或者标志性建筑时,它们转而使用地标[7-8].受这种鸽群归巢行为机制的启发,Duan等提出了一种鸽群优化算法[9](pigeon-inspired optimization,PIO),其简单、有效的特点[10]促使它得到了众多学者的重视和研究[11-12].
鸽群优化算法收敛速度快,精度高,但是与其他一些全局最优算法一样,它也有早熟收敛的现象.针对算法的这一缺陷,现在也有一些改进方法,例如Sun等将捕食者机制引入鸽群算法[13], Li等引入了模拟退火法[14],Yang等将柯西变异引入鸽群算法[15],这些改进虽然增加了种群规模或种群活跃性,但是对具有局部最优值的函数优化依然不太理想.笔者对自然界鸽子群体飞行行为进行了总结,提出了一种生物行为启发式的引入迷失探索与集群分裂机制的改进鸽群优化算法(lost and split pigeon-inspired optimization,LSPIO).新的算法以当前全局最优位置作为罗盘方向,受鸽子自然飞行过程中可能会迷失方向(感应不到罗盘),从而采用有限时间感知探索机制[16]的启发,赋予算法中个体一个迷失概率,在迷失期间鸽子会自由探索,增加算法的全局搜索能力.同时借鉴鸽子飞行过程中发生的集群分裂机制,随机分裂出若干子群进行地标探索,这样既保证了全局搜索性能,也兼顾了局部搜索性能.笔者采用9个标准测试函数测试LSPIO算法的性能,并与标准鸽群算法和粒子群算法结果进行对比分析,在多个测试函数上的结果表明,笔者提出的算法不仅具有更高的收敛性能,可以有效地避免早熟问题,并且有效提高了种群多样性.
1 鸽群优化算法介绍
在鸽群优化算法中,分别基于鸽子的太阳、地磁导航机制和地标导航机制提出了两种算子:地图罗盘算子和地标算子.在迭代优化过程中,前期使用地图罗盘算子,后期使用地标算子.
(1)地图罗盘算子:鸽子可以通过使用磁感应在大脑中塑造地图.它们将太阳的高度视为指南针来调整方向.
(2)地标算子:当鸽子靠近目的地飞行时,它们将依赖邻近的地标指示方向.
PIO模型中,每个优化问题的解都是搜索空间中的一只虚拟鸽子.每只鸽子都有一个速度矢量和位置矢量来决定它们的当前位置以及飞翔方向和距离,每只鸽子的位置所对应的目标函数值作为该鸽子的适应度(fitness value).所有鸽子个体按照一定的规则在解空间中寻找最优解,即适应度的最大值或最小值,笔者以最小值优化为例进行讨论.
在鸽群优化算法中,首先运行地图和罗盘算子,鸽子i的位置和速度分别用Xi和Vi表示,如下公式为地图和罗盘算子位置速度更新公式:
Vi(t)=rand·(Xg(t)-Xi(t-1))+
Vi(t-1)·e-Rt;
(1)
Xi(t)=Xi(t-1)+Vi(t),
(2)
式中:R是地图和罗盘因子;rand是一个随机数;Xg是当前全局最佳位置,可以通过比较所有鸽子中的所有位置来获得;t表示当前迭代次数.
地图和罗盘算子运行一段时间后,转为地标算子运行,其中远离目的地的鸽子对地标不熟悉,它们将不再有分辨路径的能力,因而被舍去,然后将剩余鸽子的中心位置Xc当作地标,所有看到地标的鸽子直接飞向地标.地标算子运行一段时间后输出最优解.地标算子的位置更新公式如下所示:
(3)
(4)
Xi(t)=rand·(Xc(t)-Xi(t-1))+Xi(t-1),
(5)
式中:fitness表示鸽子个体的适应度;Np为种群数量.
2 改进的鸽群优化算法
在鸽群优化算法运行过程中后期,如果某只鸽子发现一个当前种群最优位置,其他鸽子将迅速向其靠拢.如果该最优位置为一局部最优点,鸽群就无法在解空间内重新搜索,因此,算法陷入局部最优,出现了所谓的早熟收敛现象.
笔者结合现有研究资料和鸽群放飞实验观察发现,鸽群飞行时存在以下两个特别的行为机制:
(1)鸽子会在归巢导航过程中发生察觉不到罗盘信息而自由探索的情况,而在自由探索过程中,鸽子存在一个有限时间感知探索机制[16]:鸽子在飞行探索时不会不停转向,而是会沿一个方向飞行一段时间,如果在该时段内不能获得目标方向信息,则会选择反向或根据自身探索到的一些信息而调整方向.
(2) 由于某些外界因素(如障碍物、天敌等)的干扰,鸽群归巢过程中会发生集群分裂的情况,分裂后的子群通常会脱离主群飞行,子群飞行中可能会探索到熟悉的建筑或感兴趣的地标.
基于上述机制,笔者对鸽群算法进行改进,提出一种新的改进LSPIO算法.首先引入迷失探索机制改进地图罗盘算子以增强算法的全局搜索能力.在原有的算子基础上加入了一个迷失因子m1,表示鸽子的迷失概率.算法每次迭代都会生成一个随机数,如果该随机数小于m1则进行迷失探索操作.鸽子进入迷失状态时,会进行自由探索,首先随机产生下一时刻的速度方向,经过一定时间的探索飞行后,如果自身适应度没有向希望的方向变化,则改变飞行方向,然后重复迭代一段时间后,恢复可以探测到罗盘的状态.迷失状态时位置速度更新公式:
diffitnessi(t)=fitnessi(t)-fitnessi(t-1).
(6)
(7)
(8)
式中:Vi(t)为当前时刻速度;Vi(t-1)为上一时刻速度;Vmax为个体最大允许速度;diffitness为适应度差值;bi为适应度变化标记.每次更新位置后,如果适应度没有减少,则标记bi增加1点,连续3次适应度没有减少(即bi≥2),则更换飞行方向进行探索,如果适应度减少,则保持飞行方向探索且标记bi置零.
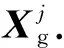
(9)
综上的鸽群优化算法,算法流程如下:
(1)初始化种群和参数,随机赋予每只虚拟鸽子的位置矢量和速度矢量并计算其适应度值,确定全局最优.
(2)判断如果迭代次数p=gencmax,则p=0,转入步骤(7),否则p=p+1,i=1并转入步骤(3).
(3)判断鸽子i的分裂状态,若处于分裂状态,则根据式(9)更新其速度和位置并转入步骤6);否则转入步骤(4).
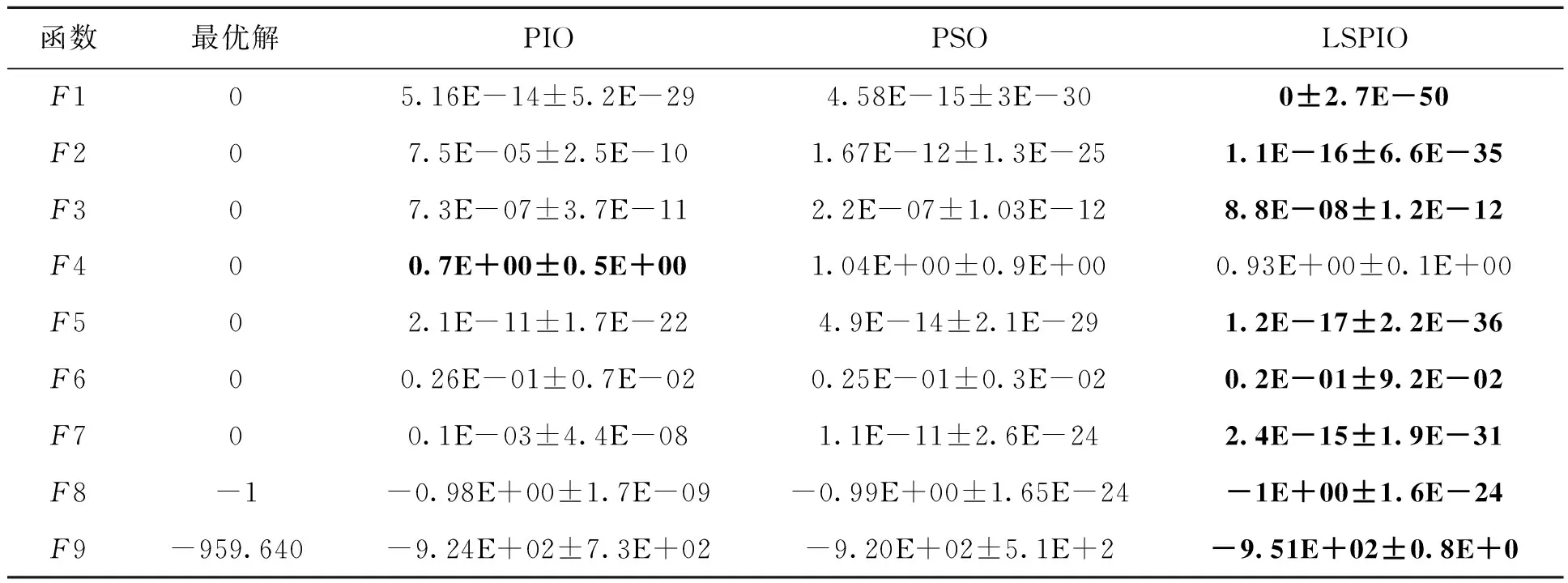
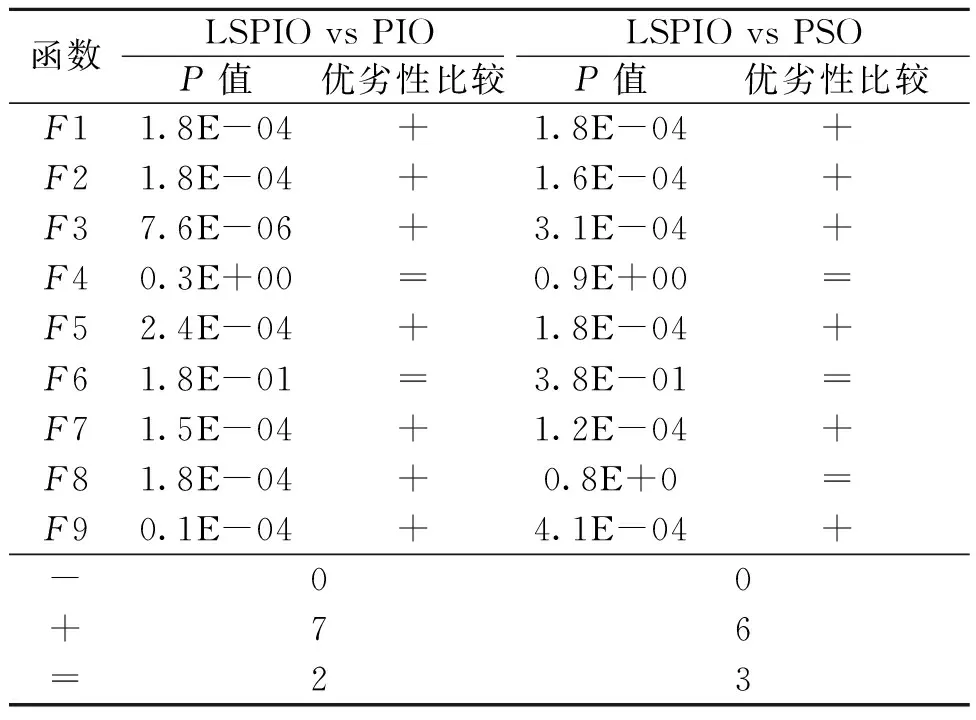
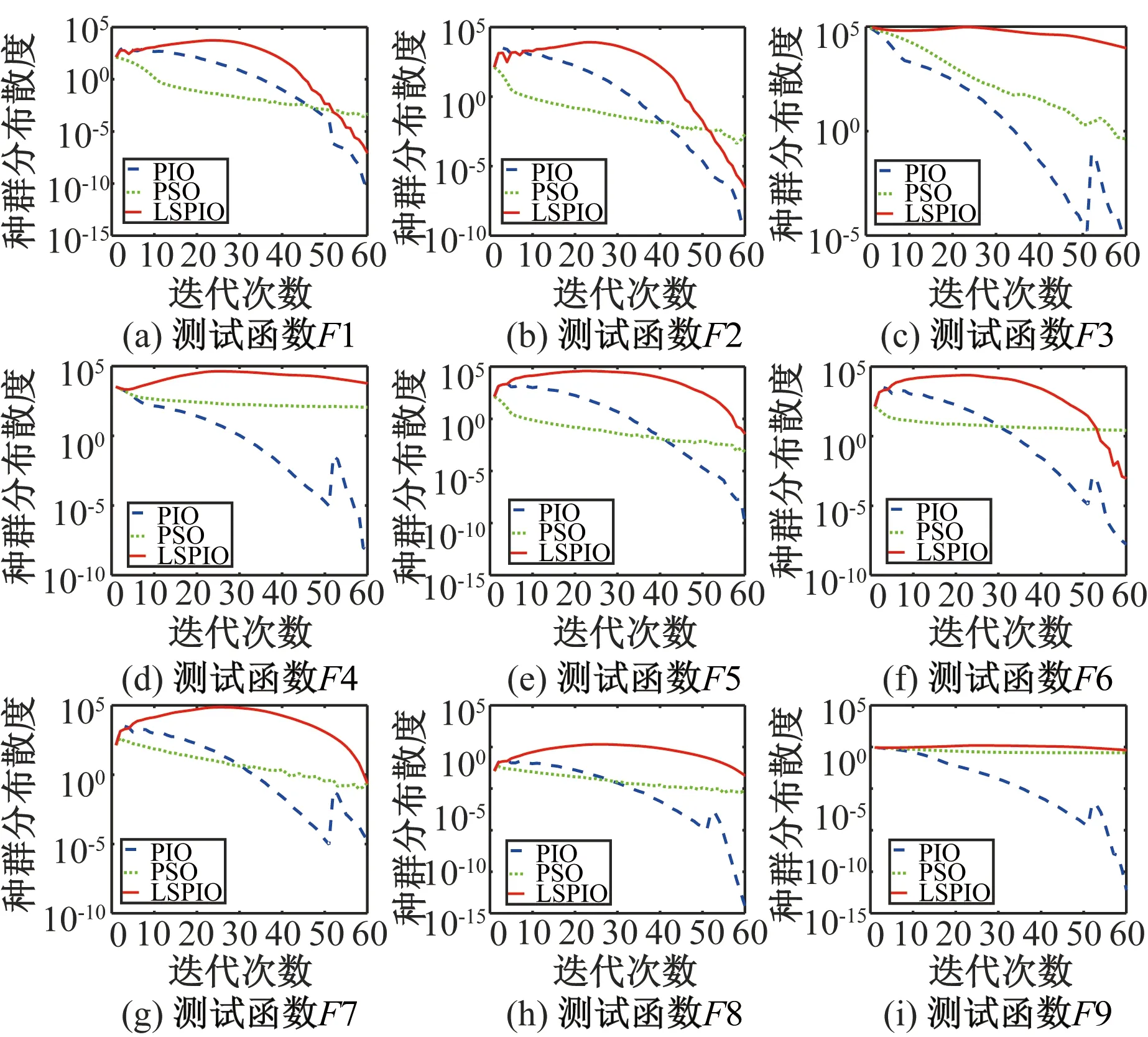
(4)生成随机数rand,判断是否rand (5)生成随机数rand,判断是否rand (6)计算鸽子适应度,i=i+1,判断是否i>Nmax,若是,转入步骤(2);否则转入步骤(3). (7)根据式(3)、(4)、(5)更新位置,计算鸽子适应度,确定最优解,迭代更新直至p=genlmax,输出结果. 算法流程图如图1所示.迷失因子m1和分裂因子m2的选取直接影响算法的收敛性能,如果选取的因子过大,则种群会有更多的机会进行探索,对全局的搜索能力更强,但收敛速度会变慢;反之收敛速度加快,但可能陷入局部最优解.笔者建议m1与m2的取值分别为0.2和0.1. 图1 LSPIO算法流程图Fig.1 Flow chart of LSPIO algorithm 为测试笔者提出的LSPIO算法的有效性,下面将通过9个典型的标准测试函数[17]展开实验,同时与PIO算法和PSO算法进行比较,3种算法种群规模和总迭代次数相同,并且在每次迭代过程中,每个个体都只评价一次个体适应度.9个测试函数公式如下,图2为测试函数三维示例图. (1) Sphere函数: (10) (2) Three-hump camel函数: 图2 测试函数三维示例图Fig.2 3D example of test function -5≤x1,x2≤5. (11) (3) Rotated Schaffers函数: (12) (4) Rotated Weierstrass函数: 其中,a=0.5;b=3;kmax=20; (13) (5) Matyas函数: -10≤xi≤10. (14) (6) Griewank函数: -600≤xi≤600. (15) (7) Levy函数: F7=2(x2-1)2(1+sin2(2πx2))+ (x1-1)2(1+sin2(3πx2))+ sin2(3πx1),-10≤x1,x2≤10. (16) (8) Easom函数: F8=cosx1cosx2· exp(-(x1-π)2+(x2-π)2), -100≤x1,x2≤100. (17) (9) Eggholder函数: -512≤x,y≤512. (18) 其中函数F1、F2、F5是较为简单的单模态函数,函数F3和F4主要考虑了平移和旋转对优化算法的影响,F6、F7、F9是具有多个局部最优的函数,F8的全局最小值较搜索空间小. 实验设置参数如下:3种算法种群大小都相同,粒子群算法(PSO)学习因子c1=2,c2=2;PIO算法地图罗盘因子R=-0.02;LSPIO算法迷失因子和分裂因子m1=0.2,m2=0.1,分别将9个测试函数当作目标函数,进行测试. 表1列出了用3种算法求解上述优化问题运行10次后得到的平均函数最优解.从表1可以看出,对于简单函数和具有局部最优陷阱函数,LSPIO算法的优化结果优于其他两种算法,而对于旋转函数,LSPIO的表现和其他两种算法相当. 图3为3种算法对函数优化10次后的平均最佳适应度演化曲线.为了验证上述结果差异是不是显著性的,笔者将上述所得数据进行假设检验.由于秩和检验[18]具有易于理解、易于计算的优点,笔者选用秩和检验进行验证.秩和检验的基本思想:若检验假设成立,则差值的总体分布应是对称的,故正负秩和不应悬殊.分别对LSPIO、PIO和LSPIO、PSO进行秩和检验,当前者优于后者并且检测P值小于0.05,则标“+”号,表示前者优于后者是显著性的.当后者优于前者并且P值小于0.05,则标“-”号,表示后者优于前者是显著性的.若检测P≥0.05,则认为它们差异不显著.表2是统计检验结果,从表2中可以看出,LSPIO在其中7个函数上的表现优于PIO,证明LSPIO比PIO收敛性能更强;而与PSO相比,LSPIO也在6个函数上表现出更优的性能.综上所述,笔者提出的LSPIO算法表现出较好的全局搜索能力,可以有效避免早熟收敛问题. 表1 3种算法运行10次平均最优解Tab.1 The average optimal solution of three algorithms with 10 runs 注:加黑字体表示最接近最优解的优化结果. 图3 最佳适应度演化曲线Fig.3 Best fitness evolution curve 函数LSPIO vs PIOLSPIO vs PSOP值优劣性比较P值优劣性比较F11.8E-04+1.8E-04+F21.8E-04+1.6E-04+F37.6E-06+3.1E-04+F40.3E+00=0.9E+00=F52.4E-04+1.8E-04+F61.8E-01=3.8E-01=F71.5E-04+1.2E-04+F81.8E-04+0.8E+0=F90.1E-04+4.1E-04+-00+76=23 注:“+”号表示LSPIO显著优越;“-”号表示PIO/PSO显著优越;“=”表示两者优劣性无显著差异. 为了评估算法的种群多样性,定义了每一代的种群分布散度,其公式为: (19) 式中:D为个体总维数;N为种群个体数. 笔者计算了迭代过程中每代种群的分布散度,如图4所示为9个测试函数分别运行10次后取平均得到的种群分布散度-迭代次数曲线.可以看出在迭代过程中,LSPIO算法的种群分布散度显著高于PSO和PIO,从而说明LSPIO算法保证了较好的种群多样性. 图4 种群分布散度演化曲线Fig.4 Evolution curve of divergence of population distribution 笔者针对鸽群优化算法的早熟收敛问题,提出了一种迷失探索与集群分裂机制的改进鸽群优化算法.这种优化算法的灵感来源于实际中鸽群飞行的迷失探索和集群分裂现象.为了测试和对比算法性能,笔者选取9个标准测试函数进行函数优化实验,并与标准鸽群算法和粒子群算法进行了对比分析,在多个测试函数上的结果表明:笔者提出的LSPIO算法具有良好的全局搜索能力,有效避免了早熟收敛问题,且较好地保持了迭代过程中的种群多样性. 笔者提出的算法虽然可以有效避免早熟收敛问题,但是它的收敛速度并不理想,并且只考虑了低维问题,接下来笔者将针对这两方面的问题进行深入研究,进一步进行算法改进以提高收敛速度和优化性能.
3 改进优化算法仿真实验
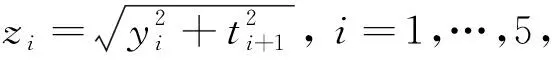

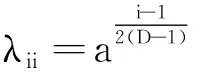

4 结论

