外中耳传声对响度感知影响的数值研究
王贺贺,刘后广,杨建华,周雷,杨善国,黄新生
外中耳传声对响度感知影响的数值研究
王贺贺1,刘后广1,杨建华1,周雷2,杨善国1,黄新生2
(1. 中国矿业大学机电工程学院,江苏徐州 221116;2. 复旦大学附属中山医院耳鼻喉科,上海 200032)
现有响度模型主要通过滤波器组在传递特性上模拟人耳感声特性,未能真实反映人耳的生理结构。基于新鲜人体颞骨标本微CT扫描影像,通过逆向成型技术及有限元法建立了基于真实生理结构的人耳模型,并基于该模型,研究外、中耳与人耳响度感知的关系。该模型主要包括耳道和中耳两个部分,通过镫骨、鼓膜脐部位移响应,镫骨速度传递函数及鼓膜处声压级对模型进行可靠性验证。最终,基于该模型,系统分析了经过外、中耳传声,传递到镫骨的镫骨底板输出位移、速度、能量与响度感知听阀曲线的关系。研究结果表明,镫骨底板输出的等速曲线及等能量曲线在中、高频段内与听阀曲线较接近,可以用于近似评估人耳在该频段内的响度感知效果。
响度;声音传导;生理模型;耳道;中耳;有限单元法
0 引言
响度是人耳对声音强弱感知的重要参数,其计算是进行声品质客观评价的基础。近年来,随着人们生活水平以及对产品性能要求的提高,人们对声品质的关注也越来越高[1],建立能够准确反映人耳感声特性的响度模型对产品的声品质预估具有重要意义。此外,响度也是助听器听力补偿研究的重要基础。由澳大利亚国家声学实验室所提出的著名NAL-NL1增益适配算法,便是基于人耳感声响度得出的[2]。因此,在设计助听装置及开发其算法的过程中,如何准确评估其对患者响度的影响至关重要。
自FLETCHER等[3]于1933年提出响度概念后,为了能够准确预估人耳感声的响度效果,国内外很多学者提出了各种响度计算模型。典型的有Stevens响度计算模型[4]、Zwicker响度计算模型[5]及Moore响度计算模型[6-7]。这些模型在机械及环境噪声评估,以及人耳感声机理的研究上做出重要贡献。但上述响度模型主要在功能上实现人耳响度测量值的逼近,通过滤波器组等实现人耳响度的计算。模型的各个部分没有真实反映人耳的生理结构[8]。
为了解决上述问题,本文基于人耳生理结构,分析人耳的外耳、中耳结构传声与人耳响度感知的关系。考虑到人耳结构具有几何超微、结构复杂的特性,集总参数等简化建模方法很难模拟,而有限单元法能够较准确地模拟人耳等复杂生物系统[9-11],为此基于微CT扫描影像及逆向成型技术,建立了包括耳道及中耳的有限元模型。并基于该模型,系统分析了经过外、中耳传声,传递到镫骨底板的输出位移、速度、能量与人耳感声等响曲线中听阀曲线的关系。研究结果为后期基于真实生理结构的人耳感声响度模型的构建奠定基础。
1 人耳传声有限元模型构建
1.1 人耳网格模型的建立
为了分析人耳结构对人耳响度感知的影响,首先建立了人耳传声有限元力学模型。该模型的实体与网格部分主要基于前期团队报道的模型[12],其构建基于新鲜的人体颞骨标本(男,60岁,右耳),采用CT扫描和逆向成型技术建成。模型包括耳道、鼓膜、听小骨(锤骨、砧骨和镫骨)以及韧带和肌腱等组织。其中,耳道采用声场单元AC3D4剖分,单元数为23 993;鼓膜(横截面积66.18 mm2)采用壳单元S3剖分,单元数为2 644;耳蜗阻抗使用十个阻尼系数为0.02 N·s·m-1的弹簧阻尼单元模拟,其中,每两个弹簧阻尼单元串联为一组,在连接点处设有5.1 mg的集中质量块。每组弹簧阻尼单元的一端固定,另一端与镫骨底板耦合[13];其余结构包括听小骨(锤骨、砧骨和镫骨)、砧锤关节、砧镫关节以及中耳支撑末端的韧带和肌腱皆采用实体单元C3D4剖分,总单元数为58 322。
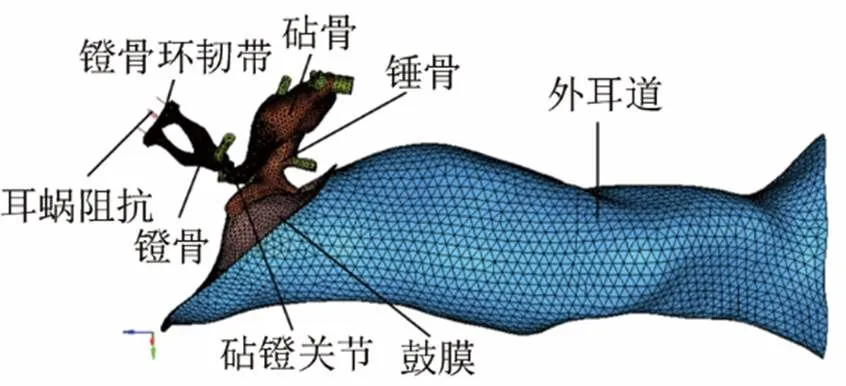
图1 基于参考文献[11]的外中耳有限元模型
1.2 材料属性
该人耳有限元模型中,模型各组织材料属性主要基于团队前期文献报道值[12]。实验研究表明,鼓膜具有粘弹性,为了使模型中组织的材料属性更接近于实际,对前期模型中的鼓膜部分进行修改,使其具有粘弹性,具体参数列于表1[14],其中,0为人耳系统不承受静态加载时的弹性模量;1为一阶松弛模量;1为一阶松弛时间。此外,为了使模型计算结果更加逼近实验值,参考文献报道的实验数据[15-17],对前期所建人耳有限元模型中部分材料参数进行微调:瑞利阻尼系数调整为=0,=1×10-4s[16];锤骨侧韧带和镫骨张肌的弹性模量分别调整为6.7、52 MPa[15];鼓膜张紧部和松弛部的弹性模量分别调整为25、10 MPa[17]。

表1 中耳软组织的粘弹性材料参数[14]
1.3 边界条件
在本文使用的人耳有限元模型中,鼓膜环韧带、中耳韧带和肌腱的端部均固定。模型的耳道流体表面定义成固壁(Wall)边界,即流体压力的法向梯度为0,并使用流固耦合的方式将耳道流体与鼓膜耦合。
2 模型可靠性验证
为了对比现有实验结果,模拟人耳传声特性,分别在模型耳道入口处及鼓膜处施加90 dB声压,进行激励。然后,通过3组数据对比,以验证模型的可靠性。值得说明的是,本文所采用的模型验证实验数据与团队之前所建模型[18]所采用的实验验证数据一致。
2.1 中耳传声验证
鼓膜脐部与镫骨底板分别对应中耳的输入、输出端,其动态响应直接反映了中耳的传递特性,故先对模型这两处的响应进行对比验证。
首先,在模型鼓膜处施加90 dB SPL的声压激励进行谐响应分析,获得了鼓膜脐部和镫骨底板的位移频响曲线(如图2所示,图中TM表示鼓膜脐部,FP表示镫骨底板),并将其与GAN等[19]实验测量值进行对比。从图2中可见,模型仿真值的幅值和趋势都与实验值较一致,能够较准确地模拟中耳的运动特性。
再通过反映中耳传递特性的镫骨底板速度传递函数,对所建模型中耳部分进行进一步验证。验证过程中,首先在模型鼓膜处施加90 dB的声压激励,进行谐响应分析,获得镫骨底板位移频响值;再按式(1)进行计算,得到镫骨底板速度传递函数[20]:
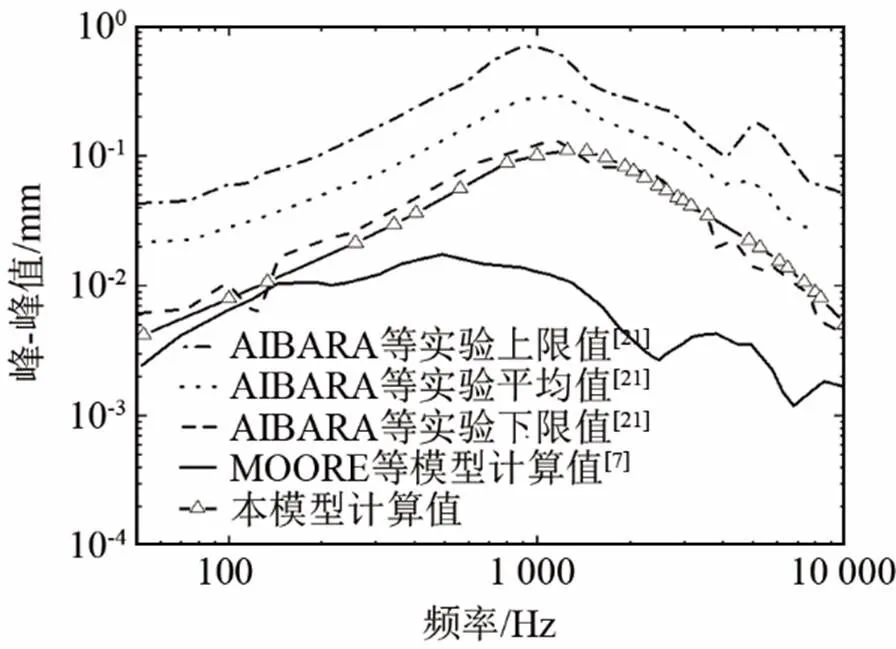
图2 实测和模型计算的鼓膜脐部和镫骨底板位移频响曲线比较
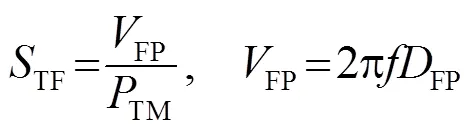

图3 实测和模型计算的镫骨底板速度传递函数频响曲线比较
此外,在图3中还增加对比了Moore团队最新响度模型的镫骨速度传递函数曲线[7],该曲线是由其构建的中耳传递函数结合AIBARA等[21]测量的耳蜗输入阻抗,推导所得。从图3中可见,Moore响度模型中的中耳部分的传声特性,与实验所测得的镫骨底板速度传递函数相差较大,尤其在中、高频段,不能准确反映人体中耳的传声特性。
2.2 耳道传声验证
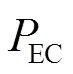
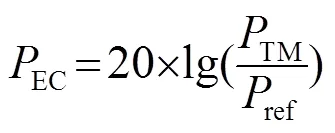
模型计算结果如图4所示,并将该结果与SHAW等[22]实验测量值及GAN等[15]模型计算值对比。从图4中可见,模型中的耳道对输入声压具有放大作用,且放大增益值随着频率而变化,在3 500 Hz处存在峰值(放大8.6 dB)。该峰值对应的频率与GAN等模型计算结果一致,但高于SHAW等实验测量值。这种在3.5 kHz处的峰值放大,主要由耳道形成的共振腔引起,与文献报道一致[23]。因此模型中的耳道能够较真实地反映耳道的传声特性。

图4 实测和模型计算的耳道入口激励下的鼓膜声压级频响曲线比较
综合对比以上3组数据可知,本文所使用的有限元模型能够较为准确地模拟耳道及中耳的传声特性,可以用于人耳传声特性研究。
3 外中耳传声对响度感知的影响
人耳感声是通过外耳、中耳将声音传递到镫骨,再由镫骨底板将声音传入耳蜗来感知声音。为了研究外耳、中耳对人耳感声响度的影响,以镫骨底板为研究对象,分别对镫骨足板的位移、速度、能量输出进行计算,下面首先对具体计算过程进行阐述。
在计算镫骨底板等位移曲线、和等速度曲线时,首先,参照等响曲线的计算方法,在模型耳道入口处施加0 dB(20 μPa)的声压激励,计算镫骨底板在1 000 Hz频率处的响应位移与速度;再以该值为标准,由模型计算出镫骨足板在其它频段输出该幅值位移、速度所需的耳道口输入声压量;最终,基于上述结果,绘制出对应的等位移曲线、等速度曲线,并将计算出的等位移曲线、等速度曲线、等能量曲线结果与国际标准听阈曲线[24]进行对比,结果如图5所示。等能量的曲线得出方法与上述相同,只是计算镫骨底板输出能量按照式(3)得出[25]:
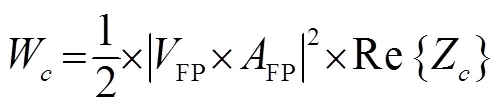
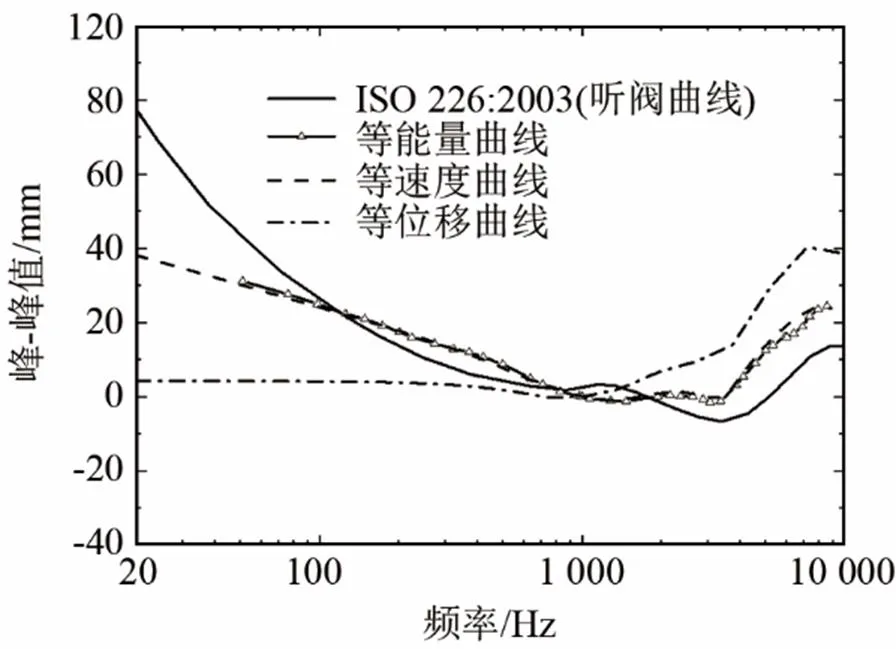
图5 等值曲线与听阈曲线的对比
由图5可见,等速度曲线和等能量曲线结果较接近,且都能较好地逼近听阀曲线的结果,而等位移曲线与响度曲线相差较大。因此,用镫骨底板输出的等速度曲线和等能量曲线能够近似评估人耳所感受到的响度。此外,模型计算的镫骨三条曲线值在低频时都低于听阀曲线值,即达到同样的听觉效果,模型所需的耳道输入在低频段更小。可见,基于外耳、中耳算出的人耳感声更灵敏,出现这种情况,主要是因为模型中没有考虑耳蜗结构。耳蜗顶端负责低频段感声[26],而该处蜗孔的存在会吸收一部分低频段的能量[27],因此不考虑耳蜗结构,会使得低频段感声更灵敏。
从图5还可以看出,模型计算出的镫骨底板等能量曲线及等速度曲线在3~4 kHz频率段内出现最低值,与响度曲线一致。该波谷反映出人耳感声在该频段更敏感,而语言频段也主要集中在该频率范围内,因此该特点将更有利于语言的理解。此外,该波谷对应频率与模型的耳道共振频率一致(如图4所示),这是由于耳道的共振放大作用所实现的。
4 结论
为了研究外、中耳传声与人耳响度感声的关系,本文采用微CT扫描影像及逆向成型技术建立了包括耳道及中耳的有限元模型,并通过对比相关的实验数据,验证了模型的可靠性。最终,利用该模型,计算并对比分析了镫骨底板输出位移、速度、能量与等响曲线中听阀曲线的关系。研究结果表明,在中、高频段,镫骨底板输出的等速度曲线、等能量曲线较接近人耳感声响度的听阀曲线,可以用于近似评估人耳的响度感知效果。此外,听阀曲线在3~4 kHz段对声音的敏感是由于耳道的共振腔放大作用引起。
[1] 毛东兴. 响度感知特征研究进展[J]. 声学技术, 2009, 28(6): 693-696.
MAO Dongxing. Recent progress in hearing perception of loudness[J]. Technical Acoustics, 2009, 28(6): 693-696.
[2] BYRNE D, DILLON H, CHING T, et al. NAL-NL1 procedure for fitting nonlinear hearing aids: characteristics and comparisons with other procedures[J]. Journal of the American Academy of Audiology, 2001, 12(1): 37-51.
[3] FLETCHER H, MUNSON W A. Loudness, its definition, measurement and calculation[J]. Bell System Technical Journal, 1933, 12(4): 377-430.
[4] STEVENS S S. Procedure for calculating loudness: mark VI[J]. J. Acoust. Soc. Am., 1961, 33(11): 1577-1585.
[5] FASTL H, ZWICKER E. Psychoacoustics-facts and models[M]. Berlin: Springer-Verlag, 2007.
[6] MOORE B C J, GLASBERG B R, BAER T. A model for the prediction of thresholds, loudness and partial loudness[J]. Journal of the Audio Engineering Society, 1997, 45(4): 224-240.
[7] CHEN Z, HU G, GLASBERG B R, et al. A new method of calculating auditory excitation patterns and loudness for steady sounds[J]. Hear Res, 2011, 282(1-2): 204-215
[8] PIEPER I, MAUERMANN M, KOLLMEIER B, et al. Physiological motivated transmission-lines as front end for loudness models[J]. J. Acoust. Soc. Am., 2016, 139(5): 2896.
[9] 姚文娟, 李武, 付黎杰, 等. 中耳结构数值模拟及传导振动分析[J]. 系统仿真学报, 2009, 21(3): 651-654.
YAO Wenjuan, LI Wu, FU Lijie, et al. Numerical simulation and transmitting vibration analysis for middle-ear structure[J]. Journal of System Simulation, 2009, 21(3): 651-654.
[10] 朱翊洲, 陈力奋, 张天宇, 等. 中耳有限元分析中内耳淋巴液作用的等效模型研究[J]. 振动与冲击, 2010, 29(7): 79-82.
ZHU Yizhou, CHEN Lifen, ZHANG Tianyu, et al. Equivalent model of cochlear lymph fluidin middle ear finite element analysis[J]. Journal of Vibration and Shock, 2010, 29(7): 79-82.
[11] 刘迎曦, 李生, 孙秀珍. 人耳传声数值模型[J]. 力学学报, 2008, 40(1): 107-113.
LIU Yingxi, LI Sheng, SUN Xiuzhen. Numerical modeling of human ear for sound transmission[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(1): 107-113.
[12] ZHOU L, FENG M L, WANG W, et al. Study on the role of ossicular joint using finite element method[J]. Journal of Mechanics in Medicine and Biology, 2016, 16(4): 1650041-20.
[13] GAN R Z, FENG B, SUN Q. Three-dimensional finite element modeling of human ear for sound transmission[J]. Annals of Biomedical Engineering, 2004, 32(6): 847-859.
[14] ZHANG X, GAN R Z. A comprehensive model of human ear for analysis of implantable hearing devices[J]. IEEE Transactions on Biomedical Engineering, 2011, 58(10): 3024-3027.
[15] GAN R Z, SUN Q, FENG B, et al. Acoustic-structural coupled finite element analysis for sound transmission in human ear pressure distributions[J]. Medical Engineering and Physics, 2006, 28(5): 395-404.
[16] SUN Q, GAN R Z, CHANG K H, et al. Computer-integrated finite element modeling of human middle ear[J]. Biomechanics & Modeling in Mechanobiology, 2002, 1(2): 109-122.
[17] PIRES F, MUYSHONDT P, DIRCKX J, et al. Sensitivity analysis of material properties on a human middle ear model based on the finite element method[C]//ASA, 2015.
[18] 姚海峰, 刘后广, 周雷, 等. 人体整耳传声有限元数值模拟[J]. 噪声与振动控制, 2016, 36(2): 61-64.
YAO Haifeng, LIU Houguang, ZHOU Lei, et al. Finite element simulation of human ears[J]. Noise and Vibration Control, 2016, 36(2): 61-64.
[19] GAN R Z, WOOD M W, DORMER K J. Human middle ear transfer function measured by double laser interferometry system[J]. Otology & Neurotology, 2004, 25(4): 423-435.
[20] 刘后广, 塔娜, 饶柱石. 人体中耳有限元法数值仿真[J]. 系统仿真学报, 2009, 21(24): 7899-7901.
LIU Houguang, TA Na, RAO Zhushi. Numerical simulation of human middle ear based on finite-element method[J]. Journal of System Simulation, 2009, 21(24): 7899-7901.
[21] AIBARA R, WELSH J T, PURIA S, et al. Human middle-ear sound transfer function and cochlear input impedance[J]. Hearing Research, 2001, 152(1): 100-109.
[22] SHAW E A G. The external ear[M]. Berlin: Springer-Verlag, 1974: 455-490.
[23] 于申, 王吉喆, 孙秀珍, 等. 耳道结构性病变对传声影响的数值研究及其临床意义[J]. 中华耳科学杂志, 2016, 14(3): 349-352.
YU Shen, WANG Jizhe, SUN Xiuzhen, et al. A numerical study on effects of auditory meatus structural lesions on sound transmission and its clinical values[J]. Chinese Journal of Otology, 2016, 14(3): 349-352.
[24] International standard organization. ISO 226: Acoustics - normal equal-loudness-level contours[S]. 2003.
[25] ROSOWSKI J J, CARNEY L H, LYNCH T J, et al. The effectiveness of external and middle ears in coupling acoustic power into the cochlea[M]. Berlin: Springer Berlin Heidelberg, 1986: 3-12.
[26] 王振龙, 王学林, 胡于进, 等. 基于中耳与耳蜗集成有限元模型的耳声传递模拟[J]. 中国生物医学工程学报, 2011, 30(1): 60-66.
WANG Zhenlong, WANG Xuelin, HU Yujin, et al. FEM simulation of sound transmission based on integrated model of middle ear and cochlea[J]. Chinese Journal of Biomedical Engineering, 2011, 30(1): 60-66.
[27] JURADO C, MARQUARDT T. The effect of the helicotrema on low-frequency loudness perception[J]. J Acoust Soc Am., 2016, 140(5): 3799.
Numerical analysis of the influence of external and middle ear on loudness perception
WANG He-he1, LIU Hou-guang1, YANG Jian-hua1, ZHOU Lei2, YANG Shan-guo1, HUANG Xin-sheng2
(1. School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, Jiangsu, China; 2. Department of Otorhinolaryngology, Zhongshan Hospital Affiliated to Fudan University, Shanghai 200032, China)
In the existing loudness model, the characteristics of the human ear are simulated by a filter set, but the physiological structure of human ear is not reflected. In this paper, based on the micro-CT scanning image of a fresh human temporal bone specimen, and by using reverse modeling technique and finite element method, a loudness model with real physiological structure is built. Then the relationship between the external and middle ear and the loudness perception is studied. This model consists of ear canal and middle ear, its validity is verified by the displacement response of stapes footplate and TM umbo, the velocity transfer function of stapes footplate and the sound pressure level at the tympanic membrane. Finally, based on this model, the relationship between the auditory threshold and the output displacement, velocity, power transmitted to the stapes footplate via ear canal and middle ear is analyzed systematically. The results show that the isovelocity and isopower curves of the stapes footplate output are close to the auditory threshold curve in the middle and high frequency band, which can be used to evaluate the loudness perception effect of the human ear in this frequency band approximately.
loudness; sound transmission; physiological model; ear canal; middle ear; finite element method
O428
A
1000-3630(2019)-03-0323-05
10.16300/j.cnki.1000-3630.2019.03.015
2018-10-24;
2018-12-05
国家自然科学基金(51775547)、上海市科学与技术委员会基金(17411962200)、江苏高校品牌专业建设工程(PPZY2015B120)资助项目
王贺贺(1994-), 男, 江苏徐州人, 硕士, 研究方向为人耳传声力学及植入式助听装置。
刘后广,E-mail: liuhg@cumt.edu.cn

