Balanced Deep Supervised Hashing
Hefei Ling,Yang Fang,Lei Wu,Ping Li, , Jiazhong Chen,Fuhao Zou and Jialie Shen
Abstract: Recently, Convolutional Neural Network (CNN) based hashing method has achieved its promising performance for image retrieval task.However, tackling the discrepancy between quantization error minimization and discriminability maximization of network outputs simultaneously still remains unsolved.Motivated by the concern, we propose a novel Balanced Deep Supervised Hashing (BDSH) based on variant posterior probability to learn compact discriminability-preserving binary code for large scale image data.Distinguished from the previous works,BDSH can search an equilibrium point within the discrepancy.Towards the goal,a delicate objective function is utilized to maximize the discriminability of the output space with the variant posterior probability of the pair-wise label.A quantization regularizer is utilized as a relaxation from real-value outputs to the desired discrete values (e.g., -1/+1).Extensive experiments on the benchmark datasets show that our method can yield state-of-the-art image retrieval performance from various perspectives.
Keywords:Deep supervised hashing,equilibrium point,posterior probability.
1 Introduction
We are living in an age of information explosion every day,hundreds of billions of images are uploaded to the internet.How to develop effective and efficient image search algorithm is becoming more and more important.In fact,the simplest way to search relevant images is sorting the database images according to the distances between the database images and the query image in the feature space,and returning the nearest images.For a database with billions of images, which is quite common today, searching linearly through a database is unimaginable due to a great deal of time and memory cost.Therefore, hashing method draws more and more attention due to its fast query speed and low memory cost[Gong and Lazebnik(2011)].
Hashing method with hand-crafted features was a hot spot in computer vision field for a long time.These hashing methods [Zhang, Zhang, Li et al.(2014); Shen, Shen, Liu et al.(2015);Lin,Shen,Shi et al.(2014)]have achieved their good performance in image retrieval by utilizing some elaborately designed features, which are more appropriate for tackling the visual similarity retrieval rather than the semantic similarity retrieval.By hashing approaches, the images as inputs are mapped to compact binary codes, which approximately preserve the data structure in the original space[Liu,Wang,Ji et al.(2012)].The cost of retrieval time and restore memory can be greatly reduced,because the images are represented by binary codes(e.g., -1/+1)instead of real-valued features.On the other hand,the recent success of CNNs in many tasks,such as image classification[Krizhevsky,Sutskever and Hinton (2012)], objection detection [Szegedy, Toshev and Erhan (2013);Meng, Rice, Wang et al.(2018)], visual recognition [Chen, Chen, Wang et al.(2014);Wu, Wang, Li et al.(2018); Wang, Lin, Wu et al.(2017)], brings more probability to tackle hashing problem.In these various tasks, the convolutional neural networks can be regarded as a feature extractor, which is driven by the objection functions that are specifically designed for the separate tasks.These promising applications of CNNs show the robustness of feature learned to scale, translation, rotation and occlusion.The feature learned by convolutional neural networks can well capture the latent semantic information of images instead of appearance differences.Because of the satisfactory performance of CNNs as a feature extractor,hashing approaches based CNNs,such as [Lai,Pan,Liu et al.(2015);Zhuang,Lin,Shen et al.(2016);Liu,Wang,Shan et al.(2016);Li,Wang and Kang(2016); Zhu and Gao (2017)], are proposed to solve hashing problem.Generally, deep hashing methods consist of two modules: i) feature extractor and ii) feature quantization that encourages the CNNs outputs to approximate the desired discrete values(e.g.,-1/+1).

Figure 1: The network architecture of BDSH consists of 5 convolution layers, 3 pooling layers and 3 fully connected layers.The objective function is elaborately designed to exploit discriminative features between image pairs and make the network outputs approximate the desired discrete values.And the binary hash codes are generated by directly quantizing the image outputs with function sign
Our goal is to map the images to compact binary hash codes and preserve the discriminability of features to support efficient and effective search simultaneously.As shown in Fig.2(a),our learning framework aims at minimizing the quantization error from the network real-valued features to the desired discrete values(e.g.,-1/+1).And meanwhile,as shown in Fig.2(b), another goal achieved by our framework is to maximize the discriminability of network outputs.Since it is extremely difficult to optimize CNNs based model by the non-differentiable loss function in Hamming space.It suggests that directly computing compact binary codes by the CNNs based model could be challenging.As shown in Fig.2,minimizing the feature quantization error in hashing can lead to the changes of feature distribution,thus inevitably reduce the discriminability of features[Zhu and Gao(2017)].Among the existing hashing methods, there always exists a discrepancy between maximizing the discriminability of network outputs and minimizing the quantization error.Inspired by this concern,we propose Deep Supervised Hashing based on variant posterior probability to support fast and accurate image retrieval , whose objective is to search an equilibrium point between the discriminability and the quantization error.In practice, a delicate objective function is proposed to maximize the discriminability of network outputs with the variant posterior probability of the pair-wise label.Simultaneously we expect that the distance between the similar image pairs is as small as possible, and the distance between the dissimilar ones is large.Meanwhile, we adopt a quantization module as a relaxation to make the network outputs approach the desired discrete values.The main contributions of this paper can be summarized as following:
· Based on posterior probability, we address the discrepancy between the quantization error minimization and the discriminability maximization.A mathematical connection between posterior probability and contrastive loss is made to better understand the overall objective function within our method.
· We propose a Balanced Deep Supervised Hashing based on variant posterior probability-an end-to-end framework, which can effectively achieve good balance between the quantization error and feature discriminability.
· Experiment studies on benchmark datasets show that BDSH can greatly outperform all existing methods to achieve the state-of-the-art performance in image retrieval tasks.
2 Related work
Existing hashing methods,including LSH[Gionis,Indyk and Motwani(1999)],SH[Weiss,Torralba and Fergus (2008)], ITQ [Gong and Lazebnik (2011)], LFH [Zhang, Zhang, Li et al.(2014)], LCDSH[Zhu and Gao(2017)]and etc, have been proposed to improve the effectiveness of approximate nearest neighbour search because of their low restore memory and high retrieval speed.And all these existing methods can be divided into two classes:data-independent hashing methods[Gionis,Indyk and Motwani(1999);Andoni and Indyk(2008)] and data-dependent hashing methods [Weiss, Torralba and Fergus (2008); Gong and Lazebnik(2011)].
In the early years, because of the lack of image data, many researchers focus on the data-independent hashing methods, which use random projections to produce hashing codes.Data-independent hashing methods, for example, Locality Sensitive Hashing(LSH) [Gionis, Indyk and Motwani (1999)], can achieve good performance with long enough codes (32 bits or even more) theoretically.However, the huge demands of bits quantization is against the motivation of hashing.To solve the limitation of data-independent hashing methods, data-dependent hashing methods are proposed.These proposed methods try to learn a hash function from training data to hash codes by data-driven methods.
Data-dependent hashing method can be further categorized into two classes: unsupervised hashing methods and supervised hashing methods.On the one hand, compared with supervised hashing methods,unsupervised hashing methods only utilize unlabelled training data to learn hashing function to produce compact hash codes.For example, Spectral Hashing (SH) [Weiss, Torralba and Fergus (2008)] defined a hard criterion for a good code that is related to graph partitioning and used a spectral relaxation to obtain a binary code; Iterative Quantization (ITQ) [Gong and Lazebnik (2011)] attempts to minimize the quantization error of mapping this data to the vertices of a zero-centered binary hypercube.RSCMVD[Wang,Lin,Wu et al.(2015a)]proposes robust subspace clustering for multi-view data by exploiting correlation consensus.WMFRW [Wang, Zhang, Wu et al.(2015)]constructs multiple graphs with each one corresponding to an individual view,and a cross-view fusion approach based on graph random walk is presented to derive an optimal distance measure by fusing multiple metrics.On the other hand,supervised hashing methods are proposed to explore complex semantic similarity with supervised learning.LBMCH[Wang,Lin,Wu et al.(2015b)]learned bridging mapping between images and tags to preserve cross-modal semantic correlation.Supervised discrete hashing (SDH) [Shen,Shen, Liu et al.(2015)], in which the learning objective is to produce the optimal binary hash code for linear classification,directly solved the corresponding discrete optimization without any relaxations.The method above learns hash function by linear projections, so it can hardly achieve satisfactory performance on linearly inseparable data.To avoid this shortcoming, Supervised Hashing with Kernels (KSH) [Liu, Wang, Ji et al.(2012)] and Binary Reconstruction Embedding(BRE)[Kulis and Darrell(2009)]are proposed to obtain compact binary code in kernels space.
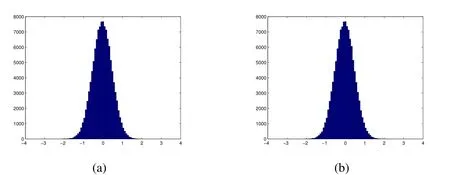
Figure 2: The distributions of network outputs in ideal case.(a) The feature distribution with minimizing quantization error and neglecting discriminability.(b) The feature distribution with maximizing discriminability and neglecting quantization error
While the above methods have certainly achieved improved retrieval performance by some extend, the features used are still based on hand-crafted features.These methods are not be able to capture the semantic structure in large-scale image data.To tackle the problem, most recently, deep learning is used to learn features and hashing function simultaneously.Deep Hashing [Liong, Lu, Wang et al.(2015)] produce a compact binary code by a non-linear deep network.Methods such as [Zhao, Huang, Wang et al.(2015); Lai, Pan, Liu et al.(2015); Zhang, Lin, Zhang et al.(2015); Wu and Wang (2018)] are proposed to learn both image feature representations and hash codes together by the promising CNNs, which have achieve improved retrieval performance.Zhao et al.[Zhao, Huang, Wang et al.(2015); Lai, Pan, Liu et al.(2015); Zhang, Lin, Zhang et al.(2015)] make use of CNNs to learn hash function, which can preserve the semantic relations of image-triplets.DSH [Liu, Wang, Shan et al.(2016)] maximize the discriminability of the output space by a contrastive loss part [Hadsell, Chopra and Lecun (2006)].And simultaneously DSH imposed a regularization on the real-valued outputs to approximate the desired discrete values by a quantization regularizer.DPSH [Li, Wang and Kang (2016)] adopted a negative log likelihood function similar to LFH [Zhang, Zhang, Li et al.(2014)] to maximize the feature discriminability, while the quantization part is used to reduce the quantization error.LCDSH [Zhu and Gao (2017)] models the hash problem as maximizing the posterior probability of the pairwise label given pairwise hash codes.However, in formula, the loss function of LCDSH is still a combination of discriminability part and quantization part.But LCDSH is prone to maximize the discriminability, which will cause huge quantization error.
By extracting pair-wise images feature and binary-like code learning, these hash methods have achieved greatly performance on image retrieval tasks.But there exist still some drawbacks about the objective function of these hash methods, which limit greatly their practical performance on image retrieval.And in the experiment section, we will show these details by a series of extensive experiments.
3 Approach
Our goal is to learn a projection P from I to B that produces compact binary codes for images such that: i) the binary codes of relevant images should be similar in Hamming space, and vice versa; ii) the binary codes should be produced efficiently.To this end, the hash codes of similar semantically images should be as near as possible, meanwhile the hash codes of dissimilar ones should be as far as possible.To keep a balance between minimizing the quantization error and maximizing the discriminability of binary codes, we propose a Balanced Deep Supervised Hashing (BDSH) method.And the network architecture of our BDSH is displayed in Fig.1.
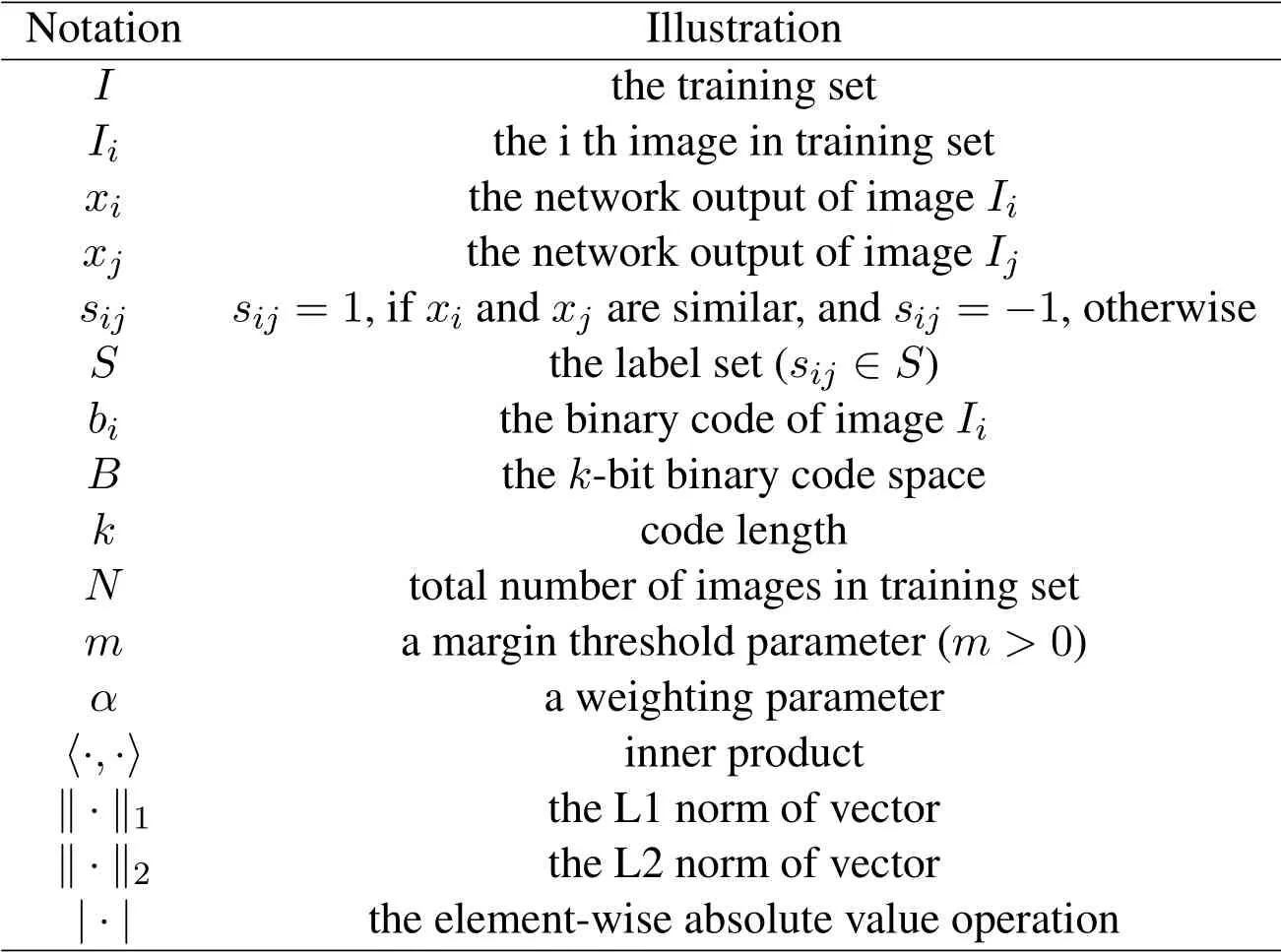
Table 1: The notation of BDSH
3.1 Loss function of BDSH
Given the pairwise similarity relationship S = {sij},the Maximum a Posterior estimation of hash codes can be represented as:

where p(S|B)denotes the likelihood function,p(B)is the prior distribution.For each pair of the images,p(sij|B)is the conditional probability of sijgiven their hash codes B,which is defined as follows:

where δ(x)=1/(1+e-x)is the sigmoid function,

Deep supervised hashing method is to learn a mapping from I to B, such that there is a suitable binary code bi∈{+1,-1}kfor each image Ii.For hashing task, semantically relevant images should be encoded to similar binary hash codes.More exactly, the binary hash codes of similar images should be as near as possible in the Hamming space,meanwhile the binary codes of dissimilar ones should be as far as possible.For this purpose,the objective function is naturally designed to pull the features of similar images close in the output space,and push the features of dissimilar ones far away from each other.So as a special variant of Eq.(3),the loss with respect to image pairs is defined as:
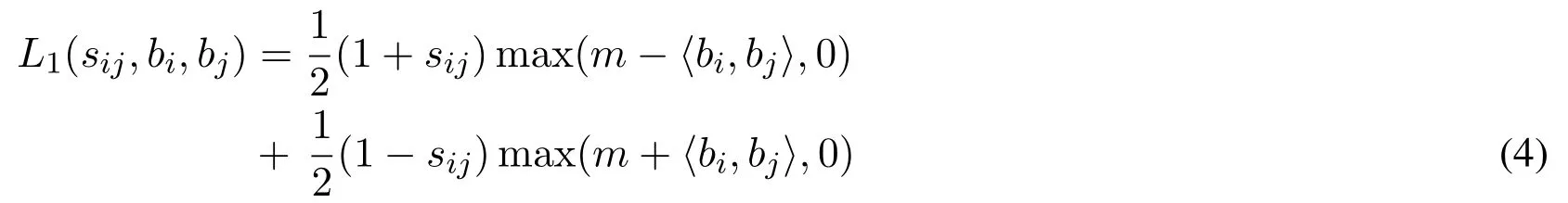
where the distance between two binary-like features is computed directly by inner product〈·,·〉,and m is a threshold parameter.The first term is to punish similar images encoded to dissimilar binary-like codes,when their distances falls below the margin threshold m.And the second term is to penalize dissimilar images encoded to similar binary-like codes.To avoid collapsed solution,only those image pairs(similar/dissimilar)keeping their distances within a range(m)are eligible to devote to the loss function.
But it is very difficult to optimize Eq.(4) directly in Hamming space.To eliminate this limitation, in this work we adopt a special regularizer that encourages the real-valued features to approximate the desired discrete codes(e.g.,+1/-1).The regularizer is defined as:

We aim to maximize the discriminability of the real-valued network outputs and minimize the quantization error from real-values to desired discrete values simultaneously.Then the whole loss function can be written as:

where α is a weight parameter to control the strength of the regularizer.Theoretically,when the α is larger,the network outputs is closer to the desired discrete values,and consequently the feature discriminability will decrease sharply.And 1 is a vector of all ones.More details will be shown in the extensive experiments.Here we use inner product 〈·,·〉 to measure the distance between network outputs directly, and L2-norm is adopted to encourage the real-valued feature to approximate the desired discrete hash codes.
With the objective function, the network model can be trained by back-propagation algorithm by Adam method (of course, mini-batch gradient descent method can also be adopted).The sub-gradients of the Eq.(6)are respectively written as:

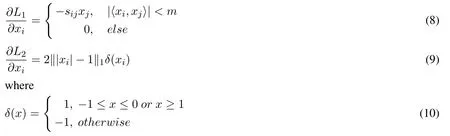
Our purpose is to minimize the overall objective function:

3.2 Implementation details
Our BDSH method is implemented with TensorFlow on a single NVIDIA 1080 GPU.The network architecture is illustrated in Fig.1.The weights layers of the last one fully-connected layers are initialized with "Xavier" initialization.In the training process,the batch size is set to 200 and epoch to 100.The learning rate of the first seven layers is set to 10-5and the last fully-connected layers to 10-4.The network is trained by back-propagation algorithm with Adam method,and beta1 is set to 0.9,beta2 to 0.999.The threshold parameter m in Eq.(4)is set to 2k (k is the hash codes length).The weighting parameter α in Eq.(6)is set to 10 to control the strength of the quantization regularizer.
4 Experiments
4.1 Datasets and evaluation metrics

Figure 3: The convergence rate and MAP result of our model on CIFAR-10.(a) The convergence rate w.r.t different number of epochs.(b) The precision-recall curves on different hash code lengths.(c)The precision with different number of top returned images
We compare our proposed model with other state-of-the-art methods on two widely used benchmark datasets: (1) CIFAR-10 [Krizhevsky (2009)].This dataset is composed of 60,000 32×32 color images,which are divided into 10 classes(6000 images per class).It is a single-label dataset,where each image belongs to one of the ten categories.The images are resized to 224×224 before inputting to the the CNN-based models.(2)NUS-WIDE[Chua,Tang, Hong et al.(2009)].This dataset has 269,648 images gathered from Flickr.It is a multi-label dataset, where each image belongs to one or multiple class labels from 81 classes.Following Liu et al.[Liu,Wang,Shan et al.(2016);Li,Wang and Kang(2016);Zhu and Gao (2017)], we only make use of the images consociated with the 21 most frequent classes, where each of these classes consist of at least 5000 images.As a result, a total of 195,834 images in NUS-WIDE are used.These images also are resized to 224×224 and then utilized as input data for these CNN-based state-of-the-art methods as well as our BDSH.In our experiments, we sample 1000 images (100 images per class) as the query set in CIFAR-10 at random.For the supervised methods, we make a random sample of 5000 images(500 images per class)from the rest images as the training set.The pair-wise label set S is constructed based on the image category label.On the other words,two images(Iiand Ij) will be considered to be similar (sij=1), if Iiand Ijhave the same label.For the unsupervised methods,we make use of the rest images as the training set.In NUS-WIDE,by following the strategy in [Xia, Pan, Lai et al.(2014)], we make a random selection of 2100 query images from 21 most frequent labels(100 images per class).For the supervised methods,we make a random sample of 10500 images(500 images per class)from the rest images as the training set.The pair-wise label set S is constructed based on the image category label.More exactly,if two images(Iiand Ij)share at least one positive label,Iiand Ijare considered to be similar(sij=1),and dissimilar otherwise.We calculate the mean Average Precision values within the top 5000 returned neighbors.
Following previous works,the mean Average Precision(MAP)for different code lengths is utilized to measure the retrieval performance of our proposed method and other baselines.
4.2 Evaluation to hyper-parameter
In this part, we validate the effectiveness of the Hyper-Parameter α and m.We test the models with α = {0,10,20,30,40,50} and m = {1,2,3,4,5} ∗k with k = 12.In Tab.2(b), we report the MAP of our method with respect to different α in CIFAR-10 and NUS-WIDE dataset.In Tab.2(a),we report the MAP of our method with respect to different m in CIFAR-10 and NUS-WIDE dataset.The retrieval MAP of different models are listed in Tab.3.And Fig.4 reports the distribution of feature on the test set of CIFAR-10 with respect to different Hyper-Parameter α, where m = 24 (k = 12).From the experiment results,we can make three observations:
· In Tab.2(a),we can observe that different m imposes little effect upon the MAP for hash codes with k =12.

Table 2: MAP of model under different setting of m and α on CIFAR-10 and NUS-WIDE
· When α=0,the features of network concentrate on 0(Fig.4(a))and we can see that the MAP is quite low on both two datasets(CIFAR-10 and NUS-WIDE)in Tab.2(b).As α grows,the network outputs gradually concentrate on-1 and+1 respectively.
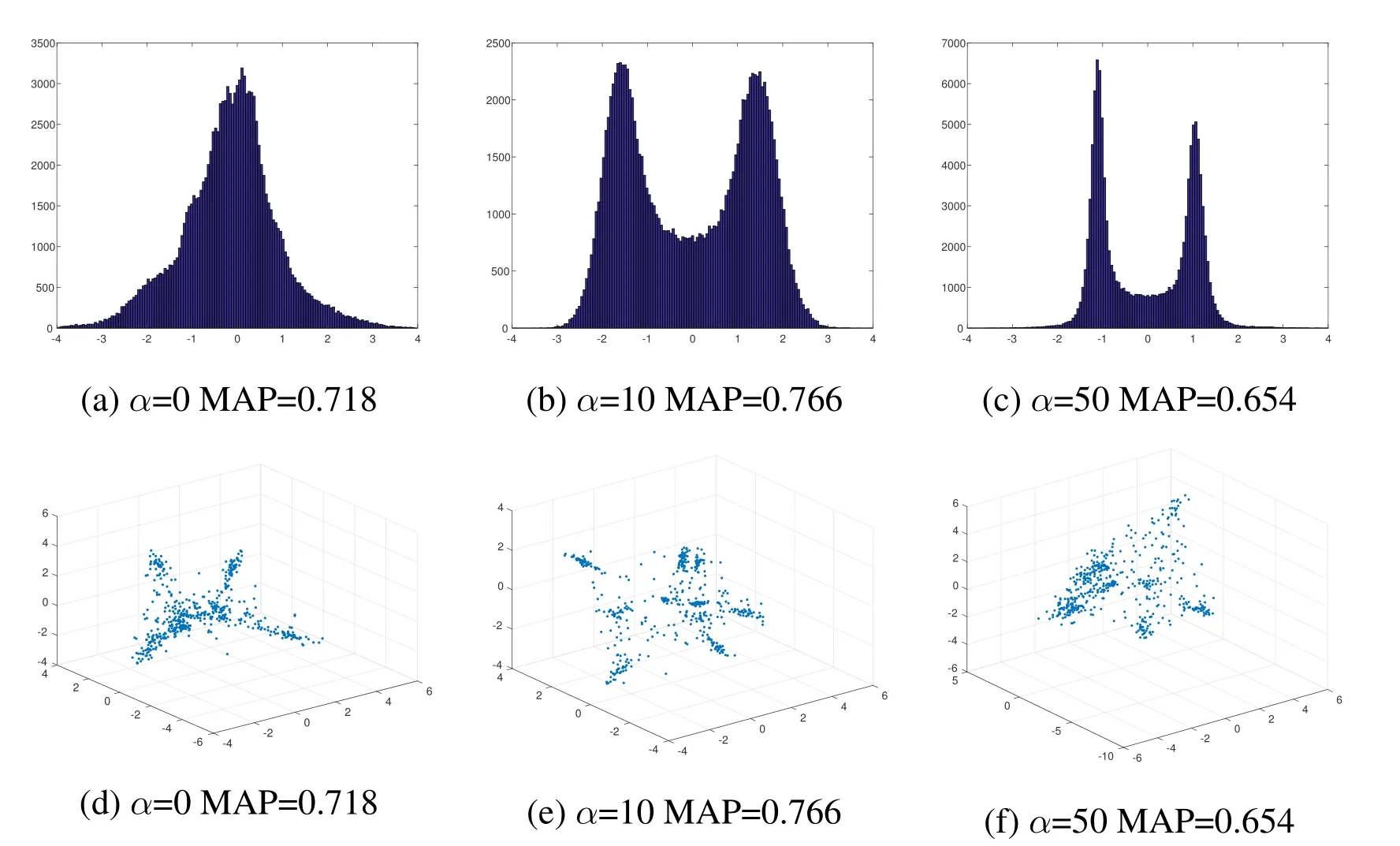
Figure 4: The distributions of network outputs under different settings of α(m = 24)on CIFAR-10
· Under proper settings of α and m, our method can generate compact hash codes for images.From Fig.4 and Tab.2(b), we can observe that the smaller α is, the more notable the discriminability of the network outputs is.And the larger α is,the closer the real-valued features is to the desired discrete hash codes.Thus there exists a discrepancy obviously of deep hashing between maximizing the discriminability and minimizing the quantization error.However,we can attempt to search an equilibrium point to keep a balance, where images can be mapped to compact binary codes by maximizing the discriminability of the network outputs and minimizing the quantization error from real-valued features to the desired discrete hash codes.
4.3 Comparison with the state-of-the-art
Comparative methods:we compare our method with a number of state-of-the-art hashing methods.These hashing methods can be divided into three categories:
· Unsupervised hashing methods with hand-crafted features, including Spectral Hashing(SH) [Weiss, Torralba and Fergus (2008)] and Iterative Quantization (ITQ) [Gong and Lazebnik(2011)].
· Supervised hashing methods with hand-crafted features,including Latent Factor Hashing(LFH)[Zhang,Zhang,Li et al.(2014)],Fast Supervised Hashing(FastH)[Lin,Shen,Shi et al.(2014)]and Supervised Discrete Hashing(SDH)[Shen,Shen,Liu et al.(2015)].
· Deep hashing methods, including Network in Network Hashing (NINH) [Lai, Pan,Liu et al.(2015)], CNNH [Xia, Pan, Lai et al.(2014)], Deep Binary Embedding Network (DBEN) [Zhuang, Lin, Shen et al.(2016)], Deep Supervised Hashing with Pairwise Labels (DPSH) [Li, Wang and Kang (2016)], Deep Supervised Hashing(DSH)[Liu,Wang,Shan et al.(2016)],Locality-Constrained Deep Supervised Hashing(LCDSH)[Zhu and Gao(2017)].
For hashing methods with hand-crafted features, each image in CIFAR-10 [Krizhevsky(2009)]is represented with a 512-D GIST feature vector.And each image in NUS-WIDE[Chua,Tang,Hong et al.(2009)]is represented by a 1134-D low level feature vector,which consists of a 64-D color histogram, a 73-D edge direction histogram, a 128-D wavelet texture,144-D color correlogram,a 255-D block-wise color moments and a 500-D bag of words based on SIFT descriptions.
For deep hashing methods,the raw image pixels are directly used as inputs,which all have been resized into 224×224.We adopt the CNN-F networks to initialize the first seven layers of our models,which is pre-trained on the ImageNet dataset[Russakovsky,Deng,Su et al.(2015)].And,the initialization strategy is same as other deep hashing methods including,DSRH[Zhao,Huang,Wang et al.(2015)],DSH[Liu,Wang,Shan et al.(2016)],DPSH[Li,Wang and Kang(2016)],LCDSH[Zhu and Gao(2017)].
The MAP of different methods on two benchmark datasets (CIFAR-10 and NUS-WIDE)is reported in Tab.3.It is observed that our BDSH greatly outperforms other baselines.Although both LCDSH and DPSH are CNN-based hashing methods with image pairs and quantization error,BDSH outperforms these two methods.
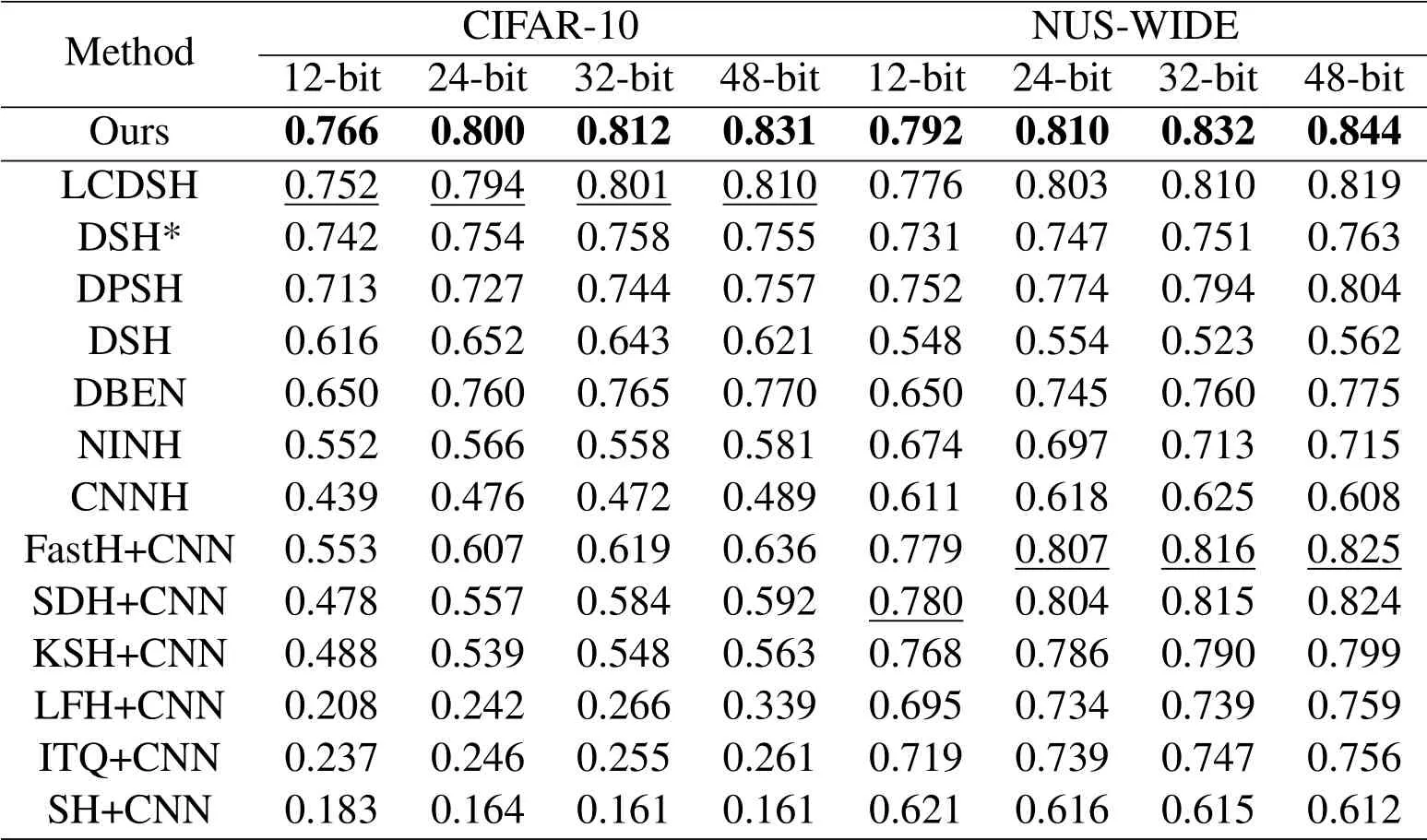
Table 3: MAP of different hashing methods on CIFAR-10 and NUS-WIDE.The MAP for two datasets is calculated based on the top 5,000 returned neighbors.DSH* denotes replacing the original network of DSH with CNN-F and then training the model by the similar initialization strategy as ours

Table 4:Training time(hours)of different hashing methods on CIFAR-10 and NUS-WIDE
Comparison of training time:Here we compare our methods with three hashing methods,including DPSH, DBEN and NINH, because only the source codes of these hashing methods are online available.Tab.4 shows the training time of different hashing methods with 12-bit code length in both CIFAR-10 and NUS-WIDE datasets.We can see that our model is faster than DBEN and NINH,and equivalent to DPSH.It is worth noting that the training time gaps between these hashing methods are due to the differences of the inputs and the framework.
4.4 Result analysis
The MAP of different methods on CIFAR-10 and NUS-WIDE is reported in Tab.3.It is observed that our method greatly outperforms other baselines.In general, these CNN-based methods greatly outperform the conventional hashing methods on these two datasets.Moreover,as shown in Tab.3,we investigate some conventional hashing methods,which are trained with deep features extracted by CNN-F network.The performance were significantly improved,but they were still inferior to our model.

Figure 5: Examples of top 10 retrieved images and precision@10 on CIFAR-10
Although,LCDSH models the hash problem as maximizing the posterior probability of the pairwise label given pairwise hash codes, the aim of LCDSH is to preserve the pairwise similarity rather than minimize the feature quantization error.Because of the discrepancy between discriminability and quantization error,LCDSH will cause huge quantization error.The distribution of LCDSH approximate extremely the distribution shown in Fig.4(a).DSH utilized a combination of contrastive loss and quantization error.However, feature quantization based hashing can lead to the change of feature distribution,which will make the feature less discriminative.For fair comparison, we replace the network of DSH with CNN-F.But the MAP of DSH*is still inferior to our method.DPSH make use of a posterior probability to measure the discriminability of image pairs,which is similar to LCDSH.As reported in Fig.4, minimizing the feature quantization error in hashing can lead to the change of feature distribution, thus inevitably reduce the feature discriminability.Instead of minimizing the quantization error or maximizing the discriminability, we attempt to search an equilibrium point within the discrepancy.Different from these deep hashing method, a combination of posterior probability and contrastive loss is made to measure the discriminability.And the distribution of BDSH is shown in Fig.4(b) and Fig.4(e).Naturally, as shown in Tab.3, our BDSH method outperforms current state-of-the-art methods on CIFAR-10 and NUS-WIDE datasets.And examples of top 10 retrieved images and precision@10 on CIFAR-10 are reported in Fig.5.BDSH can achieve effective and efficient large scale image retrieval.
5 Conclusion
In order to achieve optimal balance between maximizing the discriminability and minimizing the quantization error, we propose a Balanced Deep Supervised Hashing to achieve effective and efficient large scale image retrieval.Since the discrepancy is extremely difficult to tackle, we aim at seizing an equilibrium point to ease the conflict.To demonstrate the advantages of the proposed method, extensive experimental study has been conducted.And results show that the proposed method greatly outperforms other hashing methods.And our method is faster than conventional hashing methods in training time and retrieval effectiveness.In future work, it is interesting and promising to develop theoretical framework to optimize the performance further and apply framework to other types of data(e.g.,audio,video and text).
Acknowledgement:This work was supported in part by the Natural Science Foundation of China under Grant U1536203 and 61672254, in part by the National key research and development program of China (2016QY01W0200), in part by the Major Scientific and Technological Project of Hubei Province(2018AAA068).
 Computers Materials&Continua2019年7期
Computers Materials&Continua2019年7期
- Computers Materials&Continua的其它文章
- A DPN (Delegated Proof of Node) Mechanism for Secure Data Transmission in IoT Services
- A Hybrid Model for Anomalies Detection in AMI System Combining K-means Clustering and Deep Neural Network
- Topological Characterization of Book Graph and Stacked Book Graph
- Efficient Analysis of Vertical Projection Histogram to Segment Arabic Handwritten Characters
- An Auto-Calibration Approach to Robust and Secure Usage of Accelerometers for Human Motion Analysis in FES Therapies
- A Novel Reversible Data Hiding Scheme Based on Lesion Extraction and with Contrast Enhancement for Medical Images
