甘蓝型油菜籽水分解吸等温线及热力学性质
张雪峰 黎 斌 彭桂兰 孟国栋 罗传伟 杨 玲
(西南大学工程技术学院1,重庆 400715)(华南农业大学工程学院2,广州 510642)
种用油菜籽在储藏过程中,受其多孔介质特性、物料和储藏环境中的相对湿度以及储藏环境温度变化的影响,种用油菜籽的品质(发芽率、芽长)会受到极大的影响。而水分活度是研究其品质质量的主要因素之一,具体定义是指物料在同一绝对温度条件下的物料内部水分蒸汽压与纯水的蒸汽压力的比值[1-3]。多孔介质物料的解吸及吸附现象的产生正是由于干燥环境中的非饱和水分蒸汽压力低于多孔介质物料表面的非饱和水分蒸汽压力[4],该过程的变化随着物料内部水分蒸汽压力的变化直至达到新的平衡状态。在多孔介质内部水分蒸汽压力的变化过程中会伴随着热量的变化,进而引入净等量吸附热的概念对热量变化过程进行衡量。
近年来,大量关于食品水分吸附、解吸特性的研究已有报道[5-8]。庄棪等[9]在利用薰衣草吸附、解吸特性研究了其干燥过程动力学特性,实验考察了吸附、解吸、干燥条件对薰衣草中药用成分(总黄酮、木犀草素和芹菜素)的影响。杨昭等[10]对豌豆种子的吸附、解吸等温线及其热力学特性进行了考察,利用净等量吸附热、扩张压力、微分熵以及积分焓、熵等指标来分析豌豆种子的热力学特性,得到豌豆种子的热力学变化特性。Majd等[11]亦通过对葡萄种子的热力学特性的考察发现Peleg模型用于描述其吸附、解吸过程具有非常好的拟合性。Ouertani等[12]对木材在脱水过程中的能量需求、焓熵关系以及扩张压力等方面的参数进行考察,进而优化木材的热风干燥工艺。但是在上述关于物料吸附、解吸等温线以及热力学特性的研究报道中,鲜有对物料整体能量变化以及物料储藏稳定性的报道。
本研究针对油菜籽的解吸特性进行深入解析,在对净等量积分焓(qst)、微分熵(ΔS)、焓熵互补理论研究的基础上进一步研究种用油菜籽解吸过程中的扩张压力(Φ)、净积分焓(qin)、净积分熵(ΔSin)随水分活度(aw)以及平衡含水率(Me)的变化规律,进而深入了解种用油菜籽在储藏期间的水分与固态物质结合能的变化以及其品质降低(腐烂、发霉)的可能性。为油菜籽的干燥、储藏条件的选择和工艺参数优化提供参考。
1 材料与方法
1.1 材料
甘蓝型油菜籽(高芥酸D2品系),含水率(d.b.)为7.68%;选择品相良好(形状饱满、色泽黝黑、无裂纹)的籽粒进行实验,将样品采用人工加湿的方法[13]加湿至含水率(d.b.)35%用于实验,放置于4 ℃条件下进行密封冷藏保存。
1.2 仪器与设备
DHS-250恒温恒湿干燥箱(精度±0.1 ℃);AL-204电子天平(精度为±0.000 1 g)。
1.3 方法
考虑到油菜籽实际储藏环境的温度,实验温度选取20、30、40 ℃作为实验条件,将准备好的油菜籽样品取出迅速称量5 g作为单组样品质量,将样品放入恒重且预热至干燥环境温度的铝盒中,然后放置于干燥器的上部,干燥器下部放入预先配制好的不同浓度的硫酸溶液中,硫酸溶液用于保持干燥器中的相对湿度。提前10 min打开干燥箱预热至实验温度,减小热惯性对实验的影响。将干燥器放置于预热后的恒温干燥箱中进行脱附实验,实验过程中每隔24 h对样品进行称重,当每组实验样品的重量变化低于0.001 g时停止实验,即此时油菜籽含水率达到平衡含水率,每组实验重复3次,取平均值。
1.4 等温线数学模型
采用5种经典数学模型描述油菜籽解吸过程的aw与Me之间的关系,将实验数据用表1中的5个数学模型进行非线性拟合。并将决定系数(R2)、残差平方和(SSE)以及卡方(χ2)作为模型拟合效果的评价指标。这三个评价指标被广泛应用于干燥数学模型拟合性能评价[14,15]。
GAB模型3个参数Mm、C和K均为温度T的相关函数。Mm为物料的单层含水率,参数K、C分别为多层吸附热与单层吸附热的相关参数。各参数(Mm、C和K)与温度T的函数关系式[21]如式(1)~式(3)所示:

表1 常用油菜籽等温线数学模型[16-20]
Mm=Mm0exp[ΔH/(RT)]
(1)
C=C0exp[(HM-HN)/(RT)]
(2)
K=K0exp[(HL-HN)/(RT)]
(3)
式中:Mm0、C0、K0为模型常数项。ΔH为阿累尼乌斯能级因子/kJ/mol。HM为单层水分子吸附热/kJ/mol。HN为多层水分子吸附热/kJ/mol。HL为平均蒸汽冷凝热,本实验中取43.3 kJ/mol。R为通用气体常数,8.314 J/(mol·K);T为绝对温度/K。
油菜籽表面固体分子与空气中水分子之间所产生的范德华力是导致油菜籽吸附特性的主要原因之一。因此对油菜籽吸附表面积的分析对其水结合性质的研究具有重要作用[22],可通过式(4)进行计算:
Sa=MmAmNA/MH2O=3.53×103Mm
(4)
式中:Sa为物料表面吸附面积/m2/g;Am为水分子表面积,取1.06×10-19m2;NA为阿伏加德罗常数,3.022×1023mol-1;MH2O为纯水的摩尔质量,18 g/mol。
1.5 净等量吸附热qst与微分熵
净等量吸附热是指在一定的水分活度和温度条件下,物料内部水分向外迁移所需能量超出纯水汽化潜热的部分,通常用于设计脱水设备的基础参数设计[23]。由Clausius-Clapeyron热力学模型的推导可得表达式为[24]:
(5)
根据前人经验将净等量吸附热qst与温度T和水活度的关系简化为qst与Me的关系[25],如式(6)所示:
qst=q0exp(-Me/M0)
(6)
微分熵ΔS为物料与水分子之间的排斥力吸引力大小,与特定能级下的可获得水吸附位数量成正比[10]。ΔS与1/T和aw关系函数为:
ΔS=qst/T+Rln(aw)
(7)
式中:ΔS为微分熵/J/(mol·K);qst为净等量吸附热/kJ/mol;T为绝对温度/K;R为普适气体常数,8.314 J/(mol·K);aw为水分活度。
1.6 焓熵补偿理论
将焓熵补偿理论用于研究油菜籽脱附过程中焓与熵的变化规律,确定其水分驱动机理,净等量吸附系数与熵的线性关系式[26]如式(8)所示:
qst=TlΔS+ΔG
(8)
式中:Tl为等速温度/K;ΔG为等速温度条件下的吉布斯自由能(Gibbs free energy),用于确定化学反应的自发性,其中,ΔG<0为自发反应,ΔG>0时反应为非自发性反应/kJ/mol。
Tl和ΔG由式(8)线性拟合得到,为了检验补偿理论在油菜籽热力学特性实验中的应用,将等速温度Tl与调和平均调和温度Thm进行对比,Tl与Thm存在较大差异时,焓熵补偿理论能应用于描述驱动机理。若Tl>Thm,则表示脱附过程由焓驱动;若Tl (9) 在本实验中,等温线数量为3条,则根据式(9)可以计算出平均调和温度Thm为302.78 K。 在补偿理论的基础上对式(9)进行校正,通过补偿理论对油菜籽脱附等温线与温度之间的关系进行模拟,表达式[12]如式(10)所示: (10) 式(10)中,由于净等量吸附系数qst与平衡含水率Me存在关系,因此可变为: ΨTln(aw)=L1L2Me (11) 式中:ΨT为校正温度系数,ΨT=(1/Tl-1/T)-1;L1、L2为常数。 扩张压力Φ指为了为防止物料表面积扩大而垂直作用在物料表面任意单位长度上的作用力,代表物料表面多余的自由能,可反映油菜籽水分扩散能力,其参数计算式[27]由GAB模型得到: (12) 式中:KB为玻尔兹曼常数,1.38×10-23J/K。Am为单个水分子表面积,1.06×10-19m2。 净积分焓qin表示全部可用能,可以反映出油菜籽脱附过程中籽粒内部水分子与固态物质的结合强度,计算见式(13)。 (13) 净积分熵ΔSin表示物料内部水分(结合水、游离水)流动的无规则性和无秩序性,可以从微观层面上用于描述物料内部水分子的流动性能,利用式(14)进行计算[27]: (14) 式中:qin为净积分焓/kJ/mol;ΔSin为净积分熵/kJ/(mol·K) 对实验数据用Excel软件中进行处理,得到关于甘蓝型油菜籽在20、30、40 ℃温度条件下的解吸等温线如图1所示,可以看出:甘蓝型油菜籽的解吸等温线属于典型的第Ⅱ类曲线。在一定温度条件下,其平衡含水率Me与水分活度aw均呈正相关性,且当水分活度aw一定时,平衡含水率Me随温度的升高而降低。这类现象的出现是由于物料内部水分子在高温状态下处于活跃的激发态,比较容易脱离吸附位点,从微观角度看来这种现象表现为解吸能力增强即吸附能力降低,宏观表现即为对应的吸湿能力降低。这个发现有利于研究油菜籽安全储藏性能,比如可以采用适当的减小储藏环境的空气相对湿度即相应的水分活度、提高储藏环境温度等手段来降低油菜籽的吸湿能力和平衡含水率,进而达到延长其储藏期、降低其霉变、腐烂的概率。此表现与杨昭等[10]关于豌豆种子吸附等温线中的发现类似。 图1 油菜籽解吸等温线 将实验数据进行非线性拟合,采用五种经典等温线数学模型的(拟合性好,可解释性强,计算量少[17,18]),通过拟合结果可看出GAB模型较之其他几种模型具有更好的拟合性,GAB模型拟合各温度条件下的等温线实验数据其决定系数R2的平均值为0.993 7,卡方χ2的范围为1.396 5×10-5~0.778,残差平方和RSS最低值为4.189 6×10-6,通过对模型残差分布情况分析得GAB模型残差分布为随机分布且模型所得预测值与实验值的吻合度较高(R2=0.991 2)。综上所述,GAB模型为描述油菜籽解吸等温线的最佳数学模型。 表2 油菜籽解吸等温线模型参数及精度 图2 油菜籽平衡含水率试验值与GAB模型预测值的对比 对油菜籽脱附GAB数学模型进行拟合得到GAB模型的特征参数如表2所示。 表3 GAB拟合模型特征参数 从表3中可以看出对于参数Mm、C和K关于温度T的数学模型决定系数均大于0.96,各特征参数模型拟合良好。油菜籽的解吸过程的参数HL-HN值为负值,表明在解吸过程中,籽粒内部水分凝结热低于多层水分子的吸附热;HM-HN为负值说明油菜籽在解吸过程中水蒸气在重要的吸附位点发生了强烈的吸热反应,微观表现为水分子获得足够能量完成由内向外的迁移,宏观表现为油菜籽干燥过程中前期籽粒迅速升温,也是干燥速率急剧增大的原因,该发现从微观热力学分析方法上丰富了油菜籽的宏观干燥特特性。 根据式(4)对油菜籽吸附表面积Am进行计算,结果如表3所示。 表4 不同温度条件下的油菜籽固体吸附表面积 从表4中可以看出:在解吸过程中环境温度对油菜籽的吸附表面积有很大的影响,油菜籽固体吸附表面积均与温度呈负相关性,温度越高,其固体吸附表面积越小。这是由于在较高温度条件下,籽粒表面水分子容易脱离吸附位点,进而影响油菜籽单层含水率Mm的下降,故而固体吸附表面积Sa也下降。该发现与石启龙等[28]关于雪莲果吸附等温线中的发现类似,对于大多数食品物料而言,其固体吸附表面积的范围为100~250 m2/g,油菜籽吸附表面积亦在该区间内,说明油菜籽解吸特性与大多数多孔介质物料相似,可进一步将用于研究其他物料热力学特性的方法应用于油菜籽热力学特性的研究。 将不同温度条件下的GAB模型带入式(6)得到不同温度条件下净等量吸附热qst与平衡含水率Me的关系曲线如图3所示。 图3 不同温度条件下油菜籽平衡含水率与净等量吸附热的关系 从图3中可以看出油菜籽解吸过程中,在一定含水率Me条件下,净等量吸附热qst随温度T的升高而降低。在一定温度条件下,净等量吸附热qst与平衡含水率Me呈负相关性。当平衡含水率Me超过20.15%时,净等量吸附系数变化趋势趋于平缓。此时qst值为483.53 kJ/mol。油菜籽低平衡含水率时,籽粒外层表面吸附的是单层水分子,因而籽粒表面固体物质与单层水分子之间的较大的吸附能。赵亚等[4]也曾在花生壳/仁的吸附等温线与热力学特性研究中有类似的发现。油菜籽宏观表现为干燥中期和后期干燥速率下降,原因是水分子与固态物质之间存在较强的吸附力,干燥极为困难。与之相反的即是干燥初期含水率较高时,水分吸附位点下降,qst值较小,干燥难易程度也越低。该结论可以为油菜籽的干燥机理提供实际参考作用,例如当油菜籽干燥后期,含水率较低时,籽粒内部水分向外迁移速率大大减缓,此时可以通过一定的途径为干燥系统提供能量以保持水分子脱离吸附位点所需能量需要,进而在宏观上维持水分迁移速率。 根据对净等量吸附热qst的求解,将之带入式(7),得到微分熵(ΔS)关于含水率Me的关系曲线如图4所示。 图4 不同温度条件下油菜籽平衡含水率与微分熵的关系 从图4可以看出:一定温度条件下ΔS与平衡含水率Me呈负相关性,说明平衡含水率较低时,可用吸附位数量较多,并随着Me的增加而减少。与AVIARA等[20]关于大豆吸附平衡及热力学性质研究中发现类似。一定平衡含水率条件下,温度越高,微分熵越低。在油菜籽解吸过程中,当平衡含水率高于21.12%时,微分熵值较稳定,平均值为1.579 kJ/(mol·K),而且当含水率低于21.12%时,微分熵值明显上升,对应能级下的水吸附位数量增加,吸湿能力增强,因此可以考虑在储藏过程中进一步考虑储藏环境温度对油菜籽的影响,即提高储藏温度降低微分熵值,减少腐烂霉变等情况。对于油菜籽解吸过程,其微分熵ΔS的变化范围为1.053~9.542 kJ/(mol·K)和1.386~9.967 kJ/(mol·K)。 对净等量吸附热qst与微分熵ΔS的关系进行非线性拟合,得到不同绝对温度条件下的净等量吸附热qst与微分熵ΔS的线性关系如图5所示,等速温度Tl与吉布斯自由能ΔG如表4所示。 表5 不同温度条件下的等速温度与吉布斯自由能 图5 不同温度条件下净等量吸附热与微分熵的关系 根据式(9)计算得到在本实验中平均调和温度Thm为302.78 K,表5中在不同温度条件下的等速温度均Tl与平均调和温度Thm不相等,焓-熵补偿理论成立,可以用于分析油菜籽解吸过程的能量驱动机理。从表5中得到的拟合结果可以看出当温度为30、40 ℃时,其等速温度Tl均大于平均调和温度Thm=302.78 K,这说明在高温状态下,油菜籽的解吸过程主要由焓驱动,即水分子脱离吸附位点所需要的能量来源于系统供热。而当温度为20 ℃时,油菜籽脱附过程的Tl值分别为294.299 K与294.248 K,均低于Thm值,这说明在20 ℃温度条件下,解吸过程的能量驱动主要为熵ΔS驱动。此表现与IGLESIAS等[29]在甜菜根热力学性质研究中发现类似。 利用Origin.8.0.5软件对不同水分活度下的平衡含水率数据根据式(11)进行非线性拟合得到ΨTln(aw)与平衡含水率Me之间的关系如图6所示。 图6 不同温度条件下油菜籽平衡含水率与温度校正系数的关系 从图6中可以看出,在不同温度条件下,油菜籽解吸过程中ΨTln(aw)与平衡含水率Me呈线性关系,进一步证明补偿理论可以应用于研究温度对水分平衡性质的影响。综上所述,补偿理论可以应用于描述油菜籽温度、水分活度以及平衡含水率三者之间的关系。 在前文对各温度条件下的模型特征参数已求解的基础上,将各参数带入式(12)得到不同温度条件下扩张压力Φ与水分活度aw的关系如图7所示。 图7 不同温度条件下油菜籽平衡含水率与扩张系数的关系 从图7可以看出:在一定温度条件下,油菜籽解吸过程中的扩张压力Φ与平衡含水率Me呈正相关性;一定平衡含水率条件下,其解吸过程的扩张压力Φ随温度的增大而降低。解吸过程:Me在4.08%~28.69%范围内,Φ值的变化区间为0.096 2~ 0.171 2 J·m2。可以推断出:较高的Φ值能够提高干燥速率,而在储藏过程中,较低的Φ值能够降低水分活性,延长物料保质期,很大程度上维持油菜籽的品质。该发现与Ouertani S 等[12]和Torres M D等[25]关于木材和大豆的吸附特性研究发现相似。 在对Φ求解的基础上,选取一个特定的扩张压力,根据式(13)得到qin与Me的关系进行非线性拟合,得到其关系如图8所示,利用所求净积分焓值带入式(10)得到ΔSin与Me的关系如图9所示。 图8 平衡含水率与积分焓的关系 图9 不同温度条件下平衡含水率与积分熵的关系 从图8可以看出qin与Me均呈负相关性,平衡含水率越高,净积分焓值越低。类似结果在1976年由Iglesias 等[29]报道,该研究报道表明随着含水率的增大,物料表面单层吸附水分子变成多层吸附水分子,原有的水分子与固体表面吸附位点发生大量的位移,导致固体表面结合能的大幅度降低,水分子脱离吸附位点向外迁移所需能量降低,即固体表面对环境能量供给需求降低。因此可以将油菜籽qin与Me的变化规律归纳为,qin越高或含水率越低时,系统所需干燥能耗越大。并且在干燥过程中,随着水分子向外迁移的发生,固体表面吸附水分子结构由多层逐渐变成单层吸附水分子,而水分子与吸附位点的距离也就相应的减小,固体表面结合能大大提高,水分子脱离吸附位点所需能量变大。这也揭示了物料干燥后期干燥速率降低的本质。对于脱附过程而言,当Me低于15.36%之前,qin下降非常快,当Me高于15.36%时,qin趋于恒定,约为6.235 kJ/mol, 根据以上分析可以推断出,含水率15.36%是油菜籽干燥速率急剧下降的拐点。 从图9中可以看出,净积分熵ΔSin为负值,这是由于吸附剂本身结构在解吸过程中发生了变化[30]。在平衡含水率Me较低时,微分熵ΔSin与平衡含水率Me呈负相关性,净积分熵ΔSin在Me为5.03%、4.92%、4.88%时获得最低值分别为-72.156、-72.886、-73.468 J/(mol·K)。在各温度条件下的最低ΔSin值所对应的环境条件即为油菜籽粒内结合水和单分子层吸附水分子的最佳环境参数条件,这是因为在最低ΔSin值时,籽粒内部、表层水分子均被牢牢吸附在吸附位点,阻止了水分子与固态物质发生化学反应(霉变、腐烂等现象)影响油菜籽品质。该发现有利于油菜籽的储藏。当含水率高于上述最低净积分熵对应含水率值时,ΔSin与Me呈正相关性,Me越大,ΔSin越大。解吸过程中,Me>10.26%时温度不对ΔSin造成影响,这是由于当平衡含水率较高时,籽粒表面吸附水分子为多层分布状态,水分子与吸附位点距离较大,水分子脱离流动性较好,即ΔSin值较大时,水分子具有较大的无序性且流动性能较好,温度对其流动性的影响就不显著。在环境温度为20、30、40 ℃时,油菜籽粒内部结合水和单分子层吸附水分子各稳态参数条件如表6所示。 表6 最稳定条件 甘蓝型油菜籽的解吸等温线为典型Type Ⅱ类曲线。一定温度条件下,油菜籽的平衡含水率与水分活度成正相关性;一定水分活度情况下,油菜籽平衡含水率随温度的升高而降低。因此适当提高储藏温度或降低环境湿度可以有效地延长油菜籽的储藏期。 描述油菜籽水分活度与平衡含水率关系的最佳模型为GAB模型,不同温度条件下模型决定系数R2的平均值为0.993 7,卡方χ2的范围为1.396 5×10-5~0.778,残差平方和RSS最低值为4.189 6×10-6,通过对模型残差分布情况的分析得到GAB模型残差分布为随机分布且由模型所得预测值与实验值的吻合度较高(R2=0.991 2)。 通过对油菜籽净等量吸附热与平衡含水率关系的分析得到干燥后期qst值较大,水分子脱离吸附位点所需能量较高,干燥速率降低。因此在油菜籽干燥后期,含水率较低时,籽粒内部水分向外迁移速率大大减缓,此时可以通过一定的途径为干燥系统提供能量以保持水分子脱离吸附位点所需能量需要,进而在宏观上维持水分迁移速率。 油菜籽解吸过程中,含水率Me的增大以及温度的升高均会加大油菜籽表面过剩自由能,水分子与吸附位点的亲和力降低,使表层水分子能够更容易脱离吸附位点,宏观表现为干燥初期干燥速率变大。较高的Φ值能够提高干燥速率,而在储藏过程中,较低的Φ值能够降低水分活性,延长物料保质期,很大程度上维持油菜籽的品质。通过对净积分熵ΔSin与平衡含水率的关系分析得到油菜籽水分子与固态物质结合最紧密的最低ΔSin值,即为20、30、40 ℃条件下,油菜籽粒内结合水和单分子层吸附水最稳定条件的平衡含水率分别为5.03、4.92以及4.88%。1.7 扩张压力Φ
1.8 净积分焓与净积分熵
2 结果与分析
2.1 油菜籽等温线
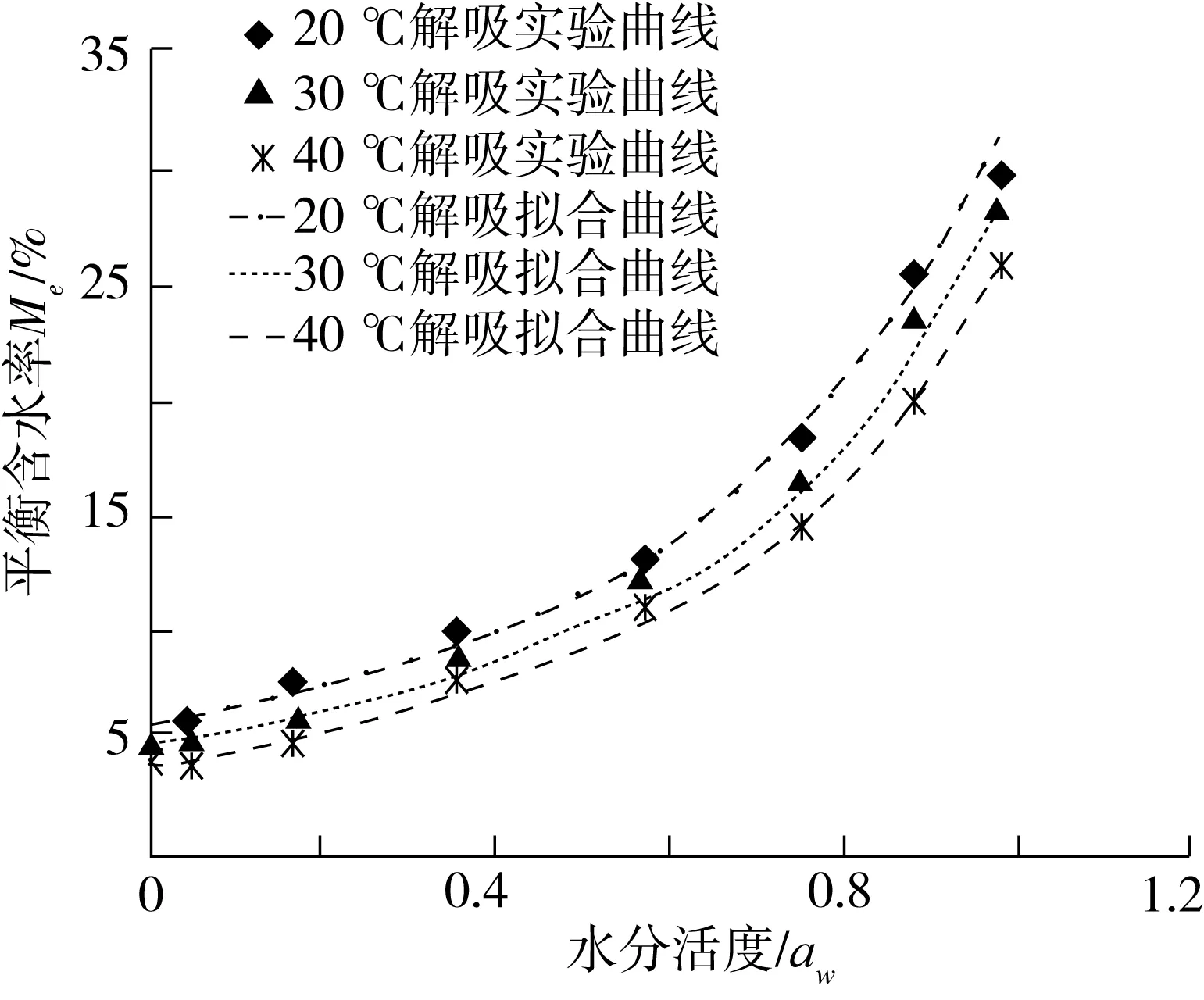
2.2 油菜籽等温线拟合模型
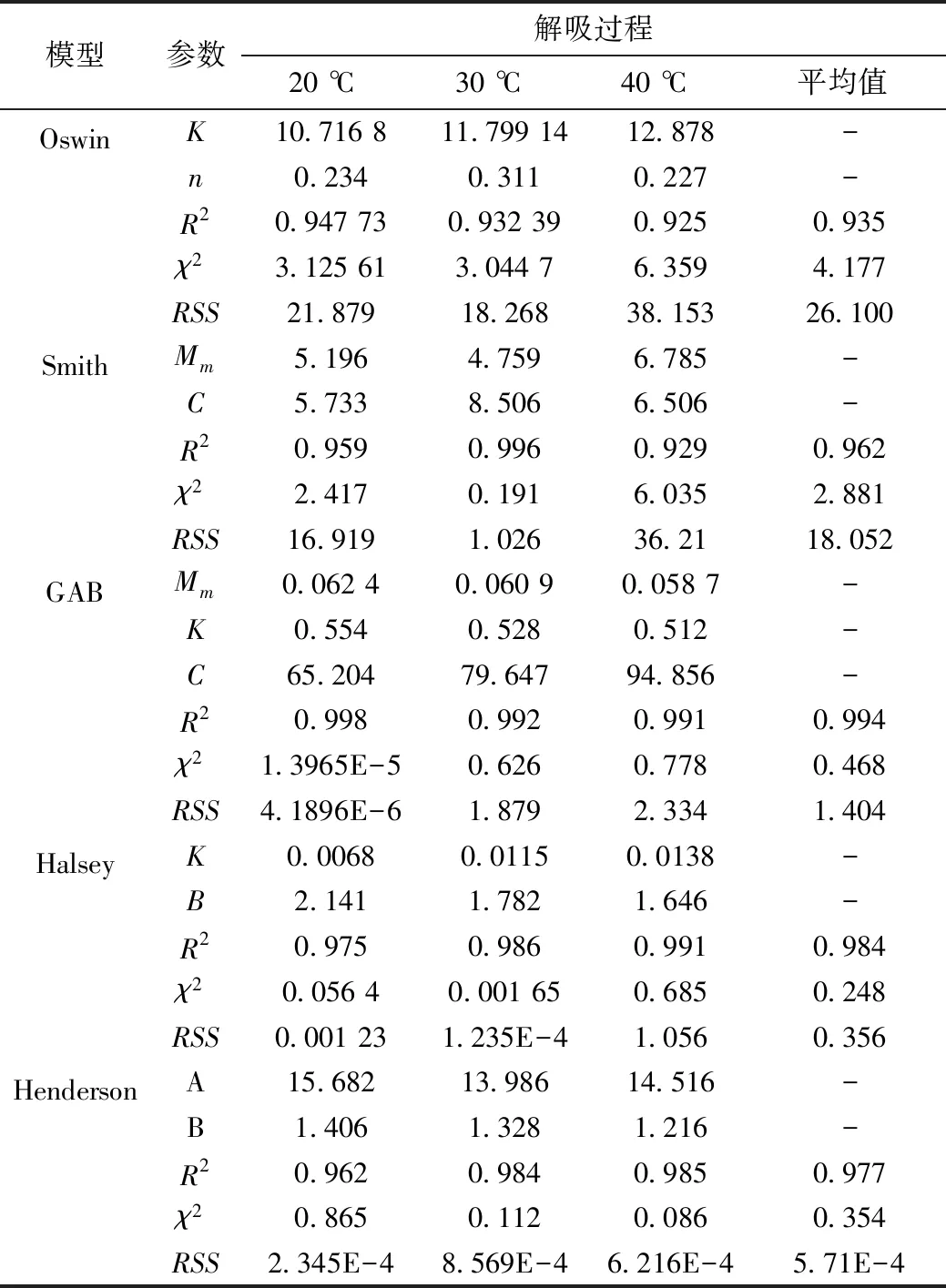
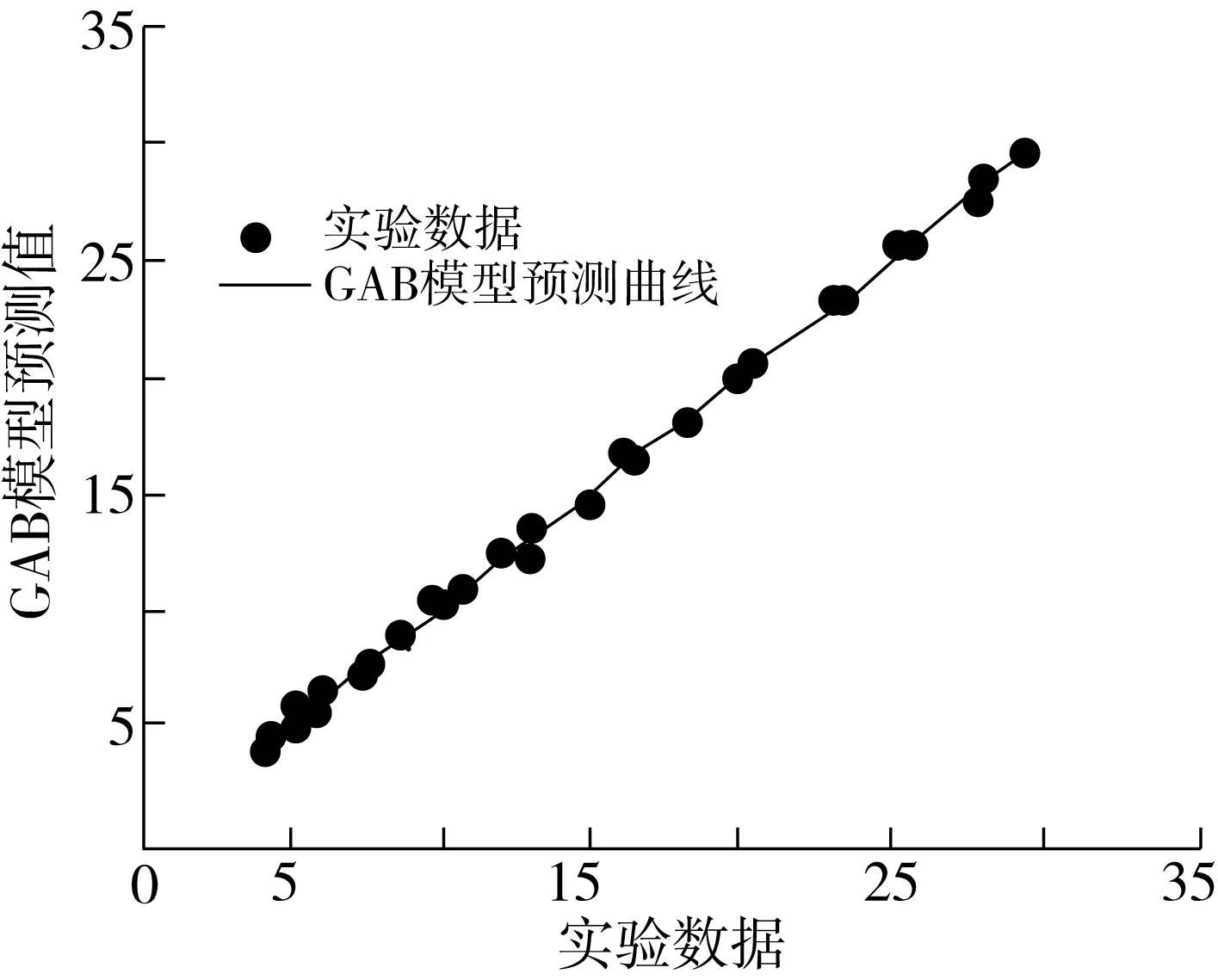
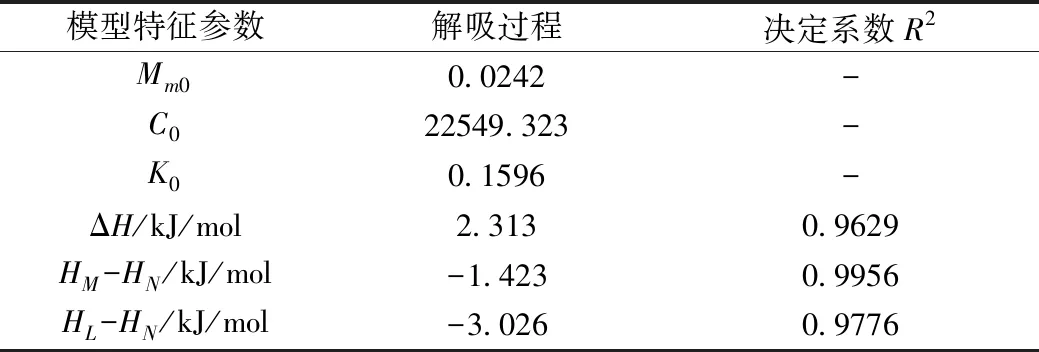

2.3 净等量吸附热
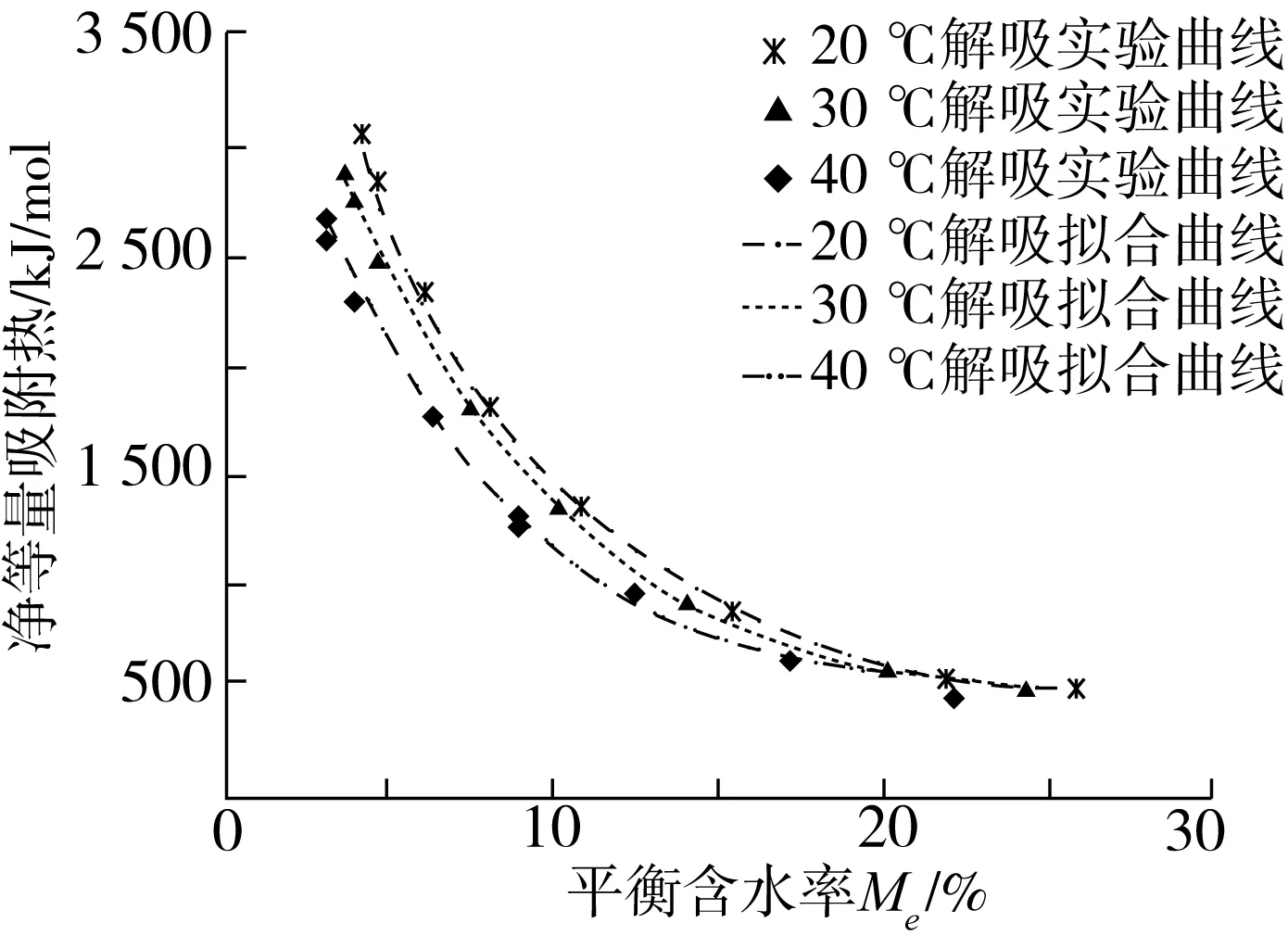
2.4 微分熵

2.5 焓熵补偿理论
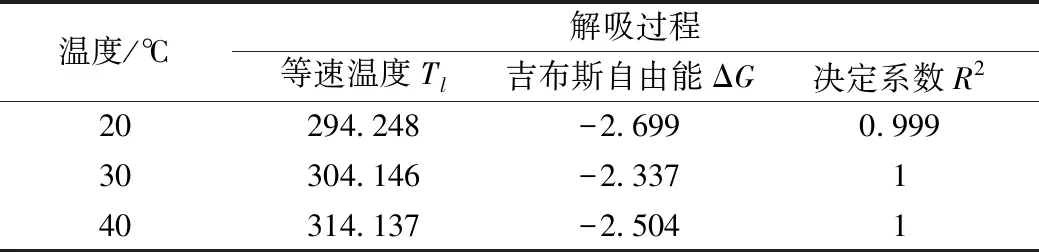

2.6 扩张压力
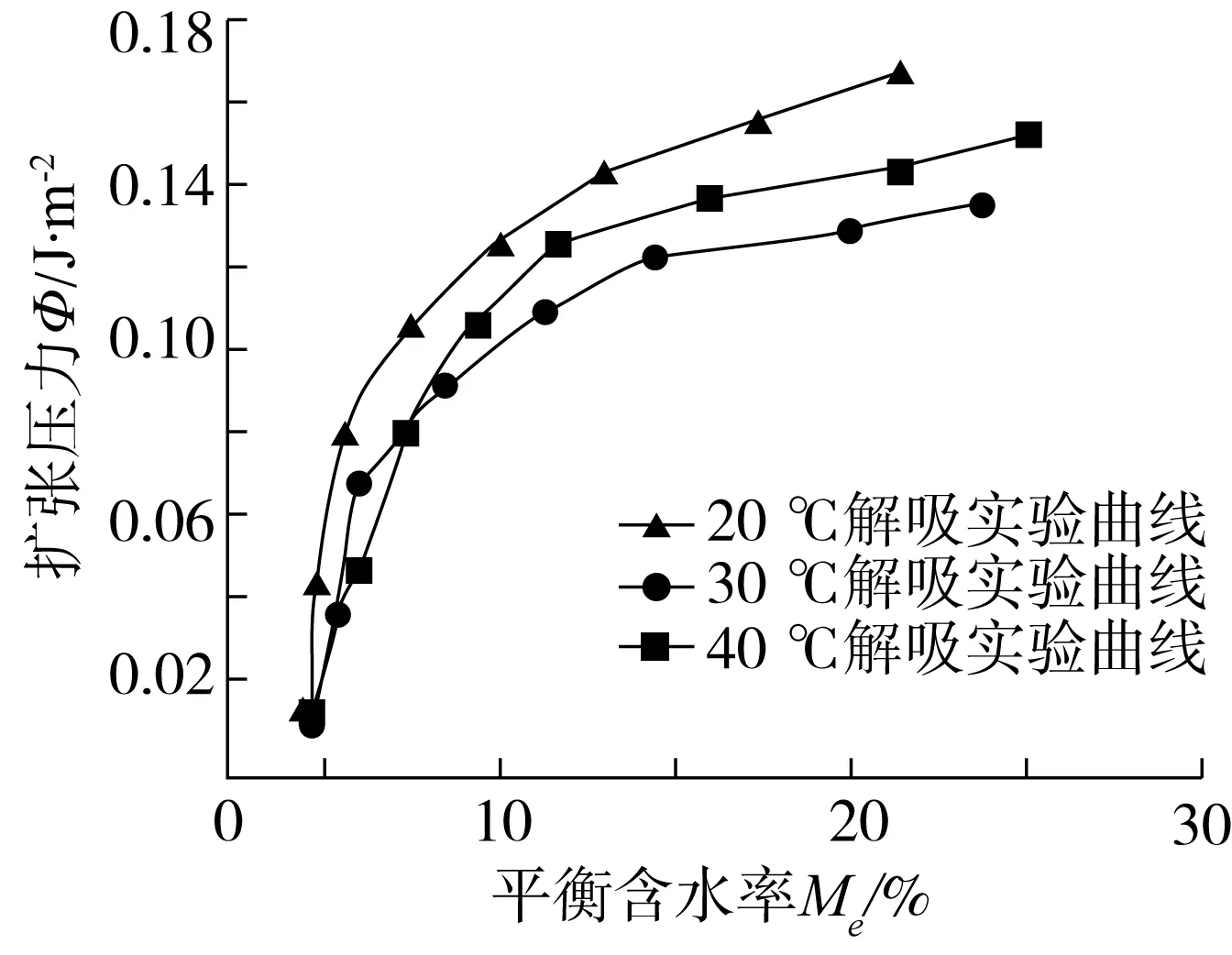
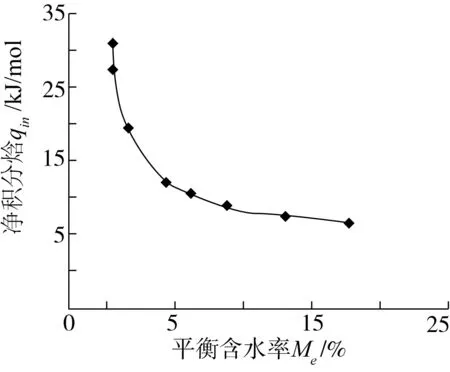
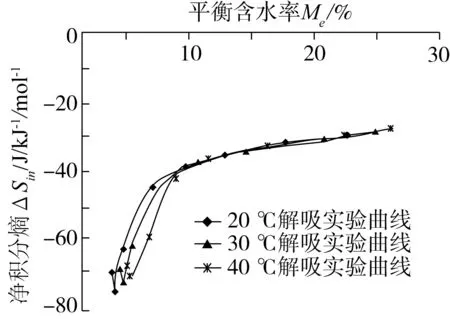
2.7 净积分焓与净积分熵

3 结论

