模糊神经网络在网络故障诊断中的应用

吴敏

摘要：从模糊系统和神经网络基本理论出发，研究其在网络故障诊断中应用的可行性、优越性，并将模糊系统和神经网络理论与故障诊断实际相结合，针对网络故障诊断中的一些具体问题应用MATLAB软件中的模糊系统工具箱和神经网络工具箱进行仿真加以解决。

关键词：模糊系统;神经网络;故障诊断;模式识别;信号处理

中图分类号：TP391.76        文献标识码：A

文章编号：1009-3044（2019）14-0174-03

Abstract： Based on the basic theory of fuzzy systems and neural networks， the feasibility and superiority of their application in network fault diagnosis are studied， and the theory of fuzzy systems and neural networks is combined with the practice of fault diagnosis. For some specific problems in network fault diagnosis， the fuzzy system toolbox and neural network toolbox in MATLAB software are used for simulation to solve the problem.

Key words：fuzzy system; neural network; fault diagnosis; pattern recognition; signal processing

1 引言

近年来，模糊理论和神经网络技术发展迅速，在军事、医学、工程、计算机、人工智能等领域应用广泛。模糊理论和神经网络技术对处理很多传统方法无法解决或在很难处理的复杂问题上具有明显优势，基于这两个学科衍生出来的边缘学科也逐步开辟出新的研究领域。

计算机网络是一个极其庞大复杂的系统工程，计算机网络和用户主机在运行过程中，都不可避免地会出现各种各样的故障，对网络故障进行及时诊断、处理，保障网络和用户主机的正常稳定运行至关重要。网络故障诊断往往异常复杂，涉及许多诸如系统建模、数据处理、信号分析、类型识别、系统仿真等繁复问题。为了能优质、高效地处理网络故障诊断中的某些复杂问题，有必要借助模糊神经网络技术以辅助网络故障的测试诊断。

2 模糊神经网络概述

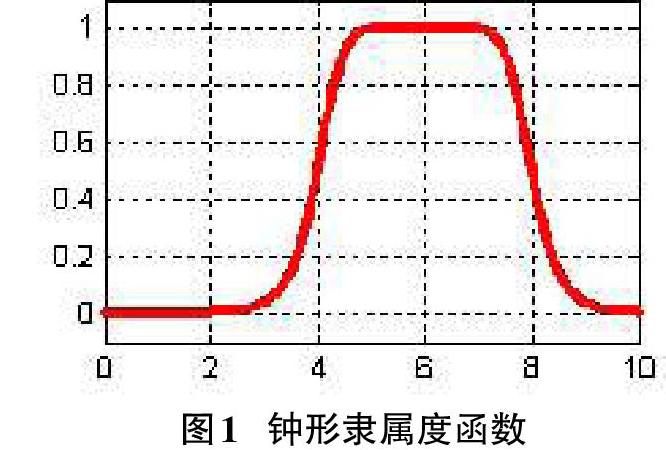
自然语言中常采用一些模糊的概念，如“网络响应时间过长”、“数据拥塞严重”等，要描述这些模糊概念并对它们进行分析、推理，需要用模糊集合和模糊逻辑来解决。与传统集合不同的是，模糊集中的一个元素可以属于该集合，也可不属于该集合，亦彼亦此，边界不分明或界限模糊。模糊逻辑认为，任何命题的真实性只是一定程度的真实性。随机性反映客观上的不确定性，或偶然性，而模糊性却反映主观理解的不确定性，即在语义理解上对事件定义或概念描述的不确定性。给定一个论域U，那么从U到单位区间[0，1]的一个映射称为U上的一个模糊集，或U的一个模糊子集。模糊集可记为A。映射μA（·）叫作模糊集A的隶属度函数。对于每个x∈U，μA（x）叫作元素x对模糊集A的隶属度。常用的隶属度函数主要有高斯型函数、钟形函数、梯形函数、三角形函数、Z形函数和sigmoid型函数等。如图1所示为钟形隶属度函数。

将给定的输入到输出的模糊逻辑映射过程称为模糊推理。模糊控制以模糊集和模糊推理为基础实现控制过程，对于那些由于被控对象过程非线性、参数间耦合强烈、随机干扰较大、过程机理错综复杂以及现场测量手段不足，或者测量手段无法进入被测区，以致不能直接获得数学模型描述的系统，可用模糊系统加以控制。模糊系统既可用于自动控制、模糊聚类，还可用于系统建模、信号处理和决策分析等许多领域，其理论基础主要是模糊推理，只是根据不同的问题采用不同的隶属度函数形式和模糊算子而已。

人工神经网络（Artificial Neural Network，即ANN ）是20世纪80 年代以来人工智能领域兴起的研究热点，在工程与学术界也常直接简称为神经网络或类神经网络。它是一种模仿动物神经网络行为特征进行分布式并行信息处理的算法数学模型，模型一般由大量神经元之间相互联接構成，每个神经元节点代表一种特定的激励函数。节点间的连接都赋予一个权重值，这相当于人工神经网络的记忆，不同的连接方式、权重值和激励函数产生不同网络输出。网络本身通常是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。神经网络的结构类型主要有：感知器、线性神经网络、BP网络、径向基函数网络、自组织竞争网络和回归网络等。

最近十多年来，人工神经网络的研究工作不断深入，已经取得了很大的进展。神经网络具有自学习、自组织、联想记忆、高速寻找优化解和并行处理等特性，在模式识别、智能机器人、自动控制、预测估计等领域已成功地解决了许多现代计算机难以解决的实际问题，表现出了良好的智能特性。

模糊理论与神经网络技术两者之间相互渗透和有机结合，促进了模糊神经网络技术的发展，也开辟了一些新的研究领域。二者结合实际上是在模拟人类大脑结构和功能，是大脑神经网络“硬件”拓扑结构和信息模糊处理“软件”思维功能的结合。两者融合主要体现在模糊系统和神经网络的简单结合、用模糊理论增强的神经网络、用神经网络增强的模糊系统和借鉴模糊系统设计的神经网络结构等方面。

利用模糊神经网络设计模型和处理问题时，往往会涉及大量数值计算，如：微分求解、最小二乘法处理、模式正交化、优化匹配等。MATLAB软件提供了模糊系统工具箱（fuzzy system）和神经网络工具箱（neural network）等软件包为解决底层工作的抽取调用提供了较大的便利。模糊系统工具箱提供了不少函数支持和建模的用户界面。神经网络工具箱以人工神经理论为基础，构造出如线性、S型、竞争层、饱和线性等典型的神经网络激活函数，可将对所选定网络输出的计算转化为调用激活函数。用户根据需要调用工具箱中的程序，可从烦琐的编程中解脱出来，直接面对需要解决的问题，从而较大的提高质效。

以模糊逻辑系统为基础的模糊模型也可用于对非线性动态建模，其中，Sugeno型模糊系统对模糊建模是非常适合的，MATLAB的模糊工具箱提供了訓练模糊系统的函数，如：genfis1，genfis2，anfis等。这类Sugeno型模糊推理系统可等效成参数，可自适应调节神经网络系统，即自适应神经网络推理系统。模糊建模过程大致可分为六个步骤：产生训练数据和检验数据;确定输入变量的隶属度函数的类型和个数;由genfis1函数产生初始的FIS结构;设定ANFIS训练的参数;利用ANFIS函数训练ANFIS;检验得到的FIS的性能。

例如对非线性函数进行逼近：f（u）=0.7sin（πu）+0.3sin（3πu）+0.1sin（5πu），仿真结果如图4所示，图中依次给出了ANFIS训练，前的隶属度函数、训练后的隶属度函数、原始的f（u）和ANFIS输出比较以及训练过程的误差。

3.5 故障检测

利用补偿模糊神经网络，可对建模系统进行故障检测。利用模糊神经网络的递归运算进行长时间的预报，不需要参考实际输出，就可在训练数据范围内提供系统的外部输入，因此，补偿神经网络模型就可以预报系统正常运行行为。如果故障发生，在比较系统的测量输出与预报输出的基础上产生残差，残差将给出实际传感器测量偏差。对残差信号进行分析，运用故障决策规则就可以进行故障检测。同时也可以利用传感器输出信息来辨识故障。

4 结束语

当前，模糊神经网络应用得越来越广泛，它不仅是一种先进的前沿技术，更是一种优越的复杂问题处理方法，发展至今已解决了许多具有挑战性的工程和理论问题，许多新的模糊神经网络模型和算法正在不断地自我丰富，对其他学科和领域的滋养更是日渐广泛和充盈。进行模糊神经网络在网络故障诊断中的应用探讨旨在抛砖引玉，希望越来越多的研究者更深入地投入到新技术新方法应用中来。

参考文献：

[1] 黄文梅.系统分析与仿真：MATLAB语言及应用[M].湖南：国防科技大学出版社，1999.

[2] 楼顺天.基于MATLAB的系统分析与设计——模糊系统[M].西安：电子科技大学出版社，2001.

[3] 闻新. MATLAB神经网络应用设计[M].北京：科学出版社，2000.

【通联编辑：代影】