Controlling Airy-Bessel Light Bullets in an Optically Induced Potential∗
Zhen-Kun Wu(吴振坤) and Yu-Zong Gu(顾玉宗)
Institute of Micro/Nano Photonic Materials and Applications,School of Physics and Electronics,Henan University,Kaifeng 475004,China
AbstractWe investigate numerically the curious evolution of self-decelerating Airy-Bessel light bullets carrying different topological charges(TC),launched in the three-dimensional(3D)Schrödinger equation with an induced parabolic potential.We present their spatiotemporal profile during propagation.In our paper,the number of TC,the modulation depth,and the induced potential are considered simultaneously.The propagation properties of light bullets result from a combination of these effects.Our scheme is distinctly different from the linear light bullets in free space,in which the localized wave packets propagate in a self-consistent trapping potential.
Key words:Airy-Bessel light bullet,self-decelerating,optically induced potential,topological charges,3D Schrödinger equation
1 Introduction
Airy beams in free space or in linear dielectric media have become an active research topic and many literature associated with this subject were published in the past decade,[1−9]the intriguing features of which were revealed as self-acceleration,self-healing,and nondi ff raction over many Rayleigh lengths.Among a quiverful of the previous literatures on Airy beam,various three-dimensional(3D)spatiotemporal wave packets or light bullet were constructed by Airy pulse in combination with other nondi ff racting field configurations.They may arise in dielectric media for a robust balance between di ff raction/dispersion and medium’s nonlinearity.The generation of light bullet is a nontrivial task from the analytical and numerical points of view,and even more complicated in real experimental settings.For example,Abdollahpour et al. have introduced the spatiotemporal Airy light bullets composed by Airy pulse in time with two spatial Airy beams.[10]To date,research on linear light bullets as solution of the 3D potential— free Schrödinger equation,including spatiotemporal Airy-Bessel light bullets,[11]Airy-Laguerre-Gaussian(AiLG)[12]wave packets,Airy-Hermite-Gaussian(AiHG)beams[13]localized wave peckets,Airy-Kummer-Gaussian(AiKG)[14]and Airy-Ince-Gaussian(AiIG)[15]light bullets,have been reported.Owing to without external potential,the reported spatiotemporal wave packets would retain their energy features over several Rayleigh lengths and other properties in free space.In addition,study of Airy light bullet is still an active topic,and recently the evolution dynamics of nonlinear Airy light bullets,and vortex-like and the Guassian-like Airy wave packets in selfdefocusing kerr medium have been reported in Refs.[16–17].
Here we are specifically concerned with what happens in an external parabolic potential—a workhorse of the introductory quantum mechanics.[3]The external parabolic potential is used in but not limited to Bose-Einstein condensates,laser-plasma physics,ultracold atoms,ion-laser interactions,and optical lattices.In this work,we simulate the propagation properties of Airy-Bessel light bullets in 3D Schrödinger equation with a self-consistent trapping potential,which has attracted little attention to the best of our knowledge.The light bullet used in the article is constructed by Airy pulse in time and a spatial 2D Bessel beam(not nonlinear mode solution),which will be the input when we execute the propagation.We demonstrate that not only the form and topological charges(TCs)of the incident light bullet but also the external parabolic potential greatly a ffect the evolution of Airy-Bessel light bullets in the medium.Its profile undergoes a profound change during propagation,which is quite different from the case in free space.
2 Theoretical Nonlinear Model and the Airy-Bessel Light Bullets
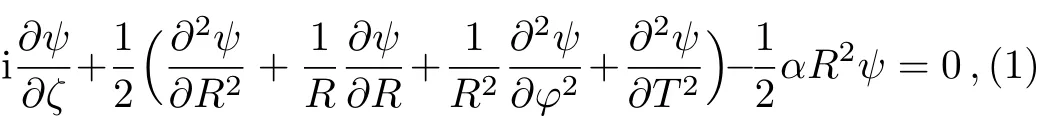
In the polar coordinate a slowly-varying spatiotemporal wave packet is considered to propagate in the dimensionless(3+1)D Schrödinger equation,evolution of which is greatly a ffected by an optical trapping potential:[11,18]in Eq.(1),the complex envelop of the beam and width of the potential,usually coming from an appropriate change in the medium’s refractive index,are represented and controlled by ψ (ζ,R,φ,T)and α,respectively.We normalize coordinatesand Y=y/w0.Here,the variables w0and t0are corresponding to the initial beam width of Gaussian beam and temporal scaling parameter,respectively.The propagation distance is normalized by ζ=z/ζRwith Rayleigh length ζR=kw02and the wave number k=2π/λ0(λ0is the vacuum wavelength).
Without considering the last term αR2/2,the solution of Eq.(1)can be written in the form ψ (ζ,X,Y,T)=ϕ(ζ,T)N(R)Φ(φ).After plugging this ansatz into Eq.(1),we end up with the following equations
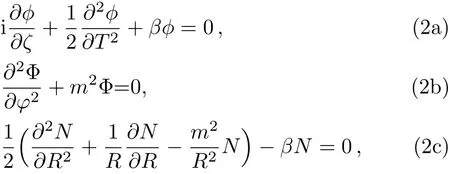
where β=0 and m(integer or half-integer)denote the separation constant and TC,[19−20]respectively.In particular,if β = −1/2,we recall that an exact analytical solution of Eq.(2)is well-known as Airy-Bessel light bullet,expressed in term of Airy and Bessel function,[21]

where

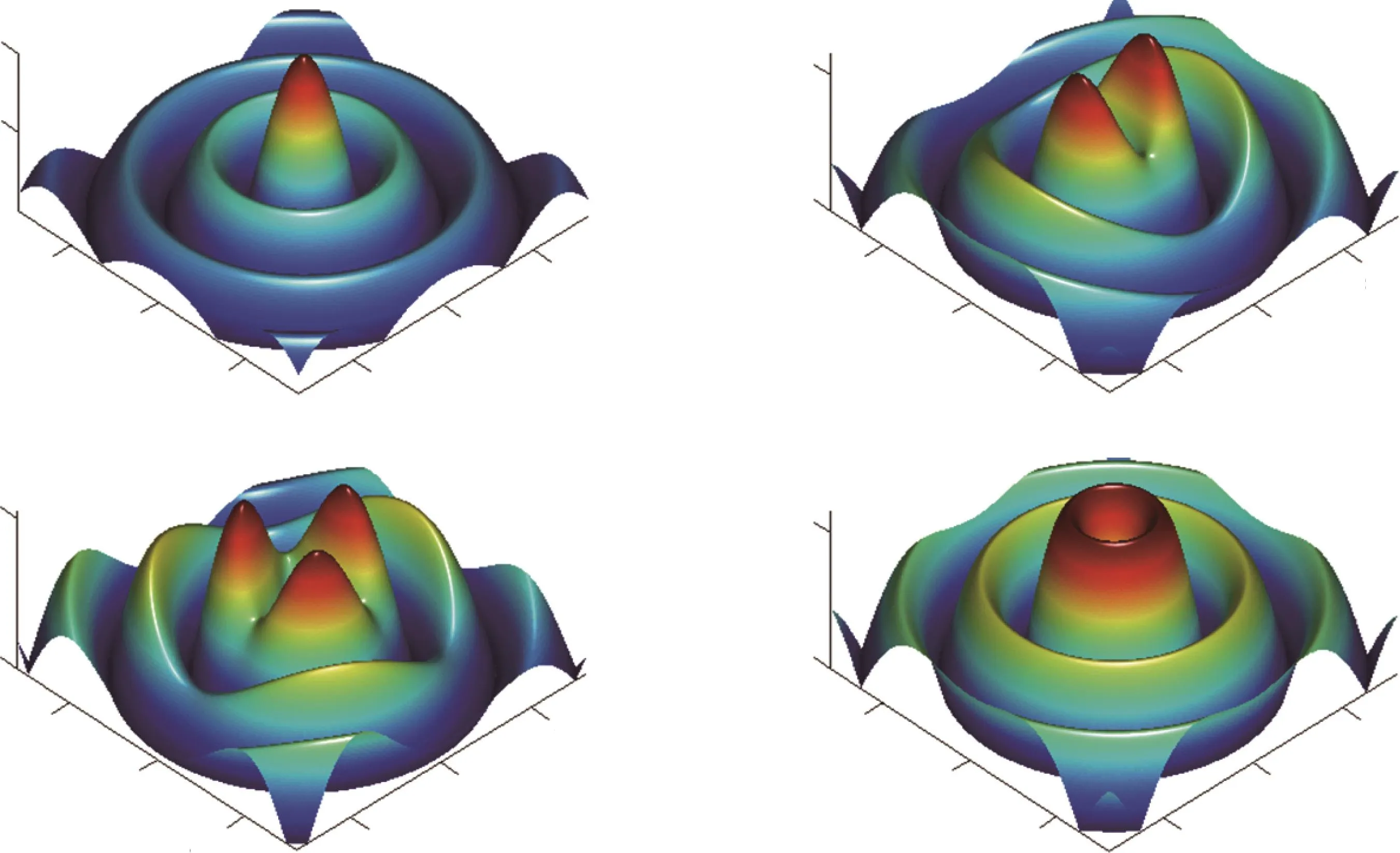
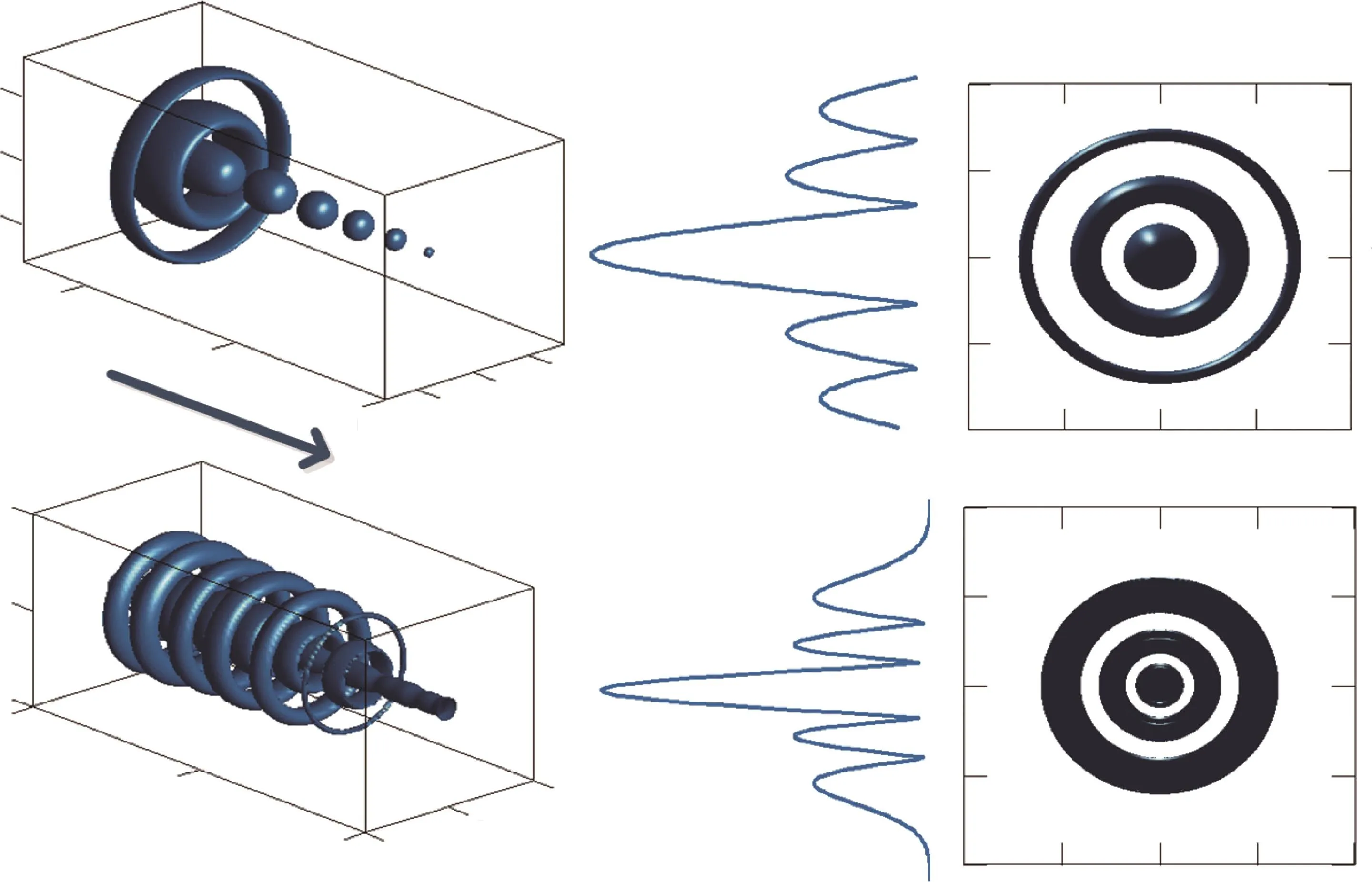
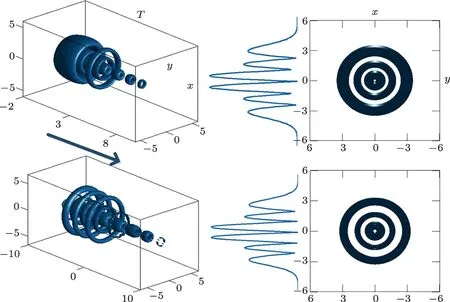
where the Ai(·)is Airy function and a is the decay parameter—a positive real number(0 Fig.1 (Color online)The intensity distributions of the finite energy Airy pulses for ϕ+(T)and ϕ− (T)for the decay parameter a=0.1. We present our results in Figs.1–5.Taking a=0.1 for instance,the intensity profiles of the finite energy Airy pulses for ϕ+(T)and ϕ−(T)are shown in Fig.1.One can see that with propagation distance the acceleration of the pulse performs in the positive(negative)T direction for σ =1(σ = −1).Clearly,attenuating slowly upon propagation,the individual pulse characterizes a long fl at tails,which enables a physical realization of the beam with finite energy.For the reason that the propagation properties of the self-accelerating Airy beam have been extensively investigated both in theory and experiment,[1,2,5,24]we only focus our attention on the self-decelerating Airy beam with σ = −1 in the following. Fig.2 (Color online)Contour plots of the optical field N(R)Φ(φ)distributions for some specific values of the TC m and modulation depth q:(a)m=0;(b)m=1,q=0.5;(c)m=1.5,q=0.5;(d)m=1.5,q=1. The common characteristic intensities of N(R)Φ(φ)modes with varying m and q are presented in Fig.2.For the case shown in Fig.2(a),the amplitude distribution features obviously azimuthal symmetric owing to azimuthal angle m=0.If m is increased to 1,the corresponding number of azimuthal node will form to make the concentric rings transform into azimuthally-modulated shapes,characterizing 2m beads,as displayed in Fig.2(b).With m=1.5,Fig.2(c)also complies the rule,while intensity distribution becomes asymmetric compared to the two former cases.Now we set q=1 and m=1,and redo the simulation presented in Fig.2(d);in comparison with the result shown in Fig.2(a),we find that the beam profile features ring-like structure and appears one singularity around the origin. To study the formation and dynamics of self-decelerating Airy-Bessel light bullets carrying different TCs m,we solve propagation Eq.(1)numerically by the fourth-order split-step fast Fourier transform(FFT)method in double precision.As initial condition,we take the expression(3)of multicharged beam perturbed by 10%of noise.To make beams of finite energy and prevent FFT spillover effects,we use an aperture with a diameter large enough to enforce fast convergence of beam intensity to zero at the transverse infinity.In the following numerical example,we set the relevant parameters to a=0.1,ω0=100 µm,λ =530 nm,α =1 and propagation distance ζ=5ζR.[12,13,21] Figure 3 displays an example of self-decelerating Airy-Bessel light bullet with m=0 in an external potential.The isosurface plots illustrate the full 3D evolution of the light bullets at ζ=0(the top row)and ζ=5ζR(the bottom row)while the right column depicts intensity distribution in the T=0 plane.As presented by the 3D plot of incidence light bullet,combination of the fundamental Gaussian state with the finite-energy Airy pulse,it is characterized by ellipsoidal pulses stacked in the vertical direction and appearance of two coaxial ring around the first pulse.Owing to m=0,there do not exist necklace ellipsoids.Obviously,from the isosurface intensity at ζ=5ζR,we find that the pulse stacked of light bullet become compressed and their shape su ff er signi fi cantly change during propagation.This phenomenon originates from the phase transition that an Airy profile is transformed into a Gaussian one at a critical point upon propagation due to the manipulation of induced potential.[16,25−27]It is a consequence of the beam approaching and bouncing o ffthe potential wall.The beam looses its multi-peak profile and propagates as a symmetric Guassian profile.This behaviour is clearly different from the results obtained in free space,[12−15,21]in which the structure of such wave packet propagates over Rayleigh lengths without appreciable change in their properties.In addition,it should be emphasized that the pulse interval is crucial difference between ζ=5ζRand ζ=0.Specifically,the pulse interval ranges from−10 to 10 in former case,while in later case it ranges from 0 to 8.As expected,this indeed shows that the light bullet is decelerating,which is accelerating in the direction opposite to the blue arrow.These results are similar to the results presented in Ref.[26]. Fig.3 (Color online)Isosurface intensity contour plot of the fundamental self-decelerating Airy-Bessel light bullet with m=0 at ζ=0(top row)and ζ=5ζR(bottom row).Figures in the column right present the vertical view in the T=0 plane from directly above.The blue arrow depicts the direction of acceleration. Let us focus on the case in which the vortex-shaped field structure is constructed with q=1 and m=1.As shown in Fig.4,the top isosurface plot represents the initial beam profile at ζ=0.In comparison with those shown in Fig.3,we if nd that the central ellipsoidal pulses change into vortex rings.The underlying physics in this setup is fundamentally different from the previous setup.The term cos(mφ)+iq sin(mφ)=eiφis ful fi lled in Eq.(3)under the condition q=1 and m=1.Thus,the phase distribution appears one singularity(called the vortex core)and energy flow around it,while the intensity is equal to zero at singularity point.[26]This is for the reason that along T axis the intensity structure is characteristic of vortex rings,as depicted in second subplot of Fig.4.The patterns at propagation distance ζ=5ζRare displayed in the bottom row.We find that it shares the dynamical behaviour of former case with m=0 and can also be explained by the reason discussed before. Fig.4 (Color online)Vortex Airy light bullets with,m=1 and q=1.Setup is the same as in Fig.3. Last,but not the least,the necklace Airy-Bessel light bullets can be obtained by setting parameters to be q=0 and m=0 in Eq.(3),as illustrated in Fig.5.Owing to the number of TC m=0,the disk-shaped fundamental pulse in each layer are transformed into necklace form with 2m beads,and the intensity structure involves 3D necklace beams.More specifically,as presented in the first subplot of Fig.5,for m=1,the structure is fragmented with fi ve layers in T-axis,and two(2m)necklace ellipsoids in the(x,y)plane in each layer.It comes from the TC dependence in Eq.(3).The second subplot displays the pattern of numerical simulation at ζ=5ζR.The manipulation of the induced potential also results in profound shape change that in the vertical direction the necklace light bullet feature distinct compressed and more layers are appeared with increase of propagation distance. In Fig.5,if TC m is set as half-integer and limit q=0,we do the corresponding simulations and the results are shown in the bottom row,i.e.,an example of the asymmetric necklace pattern.Compared with the results obtained in the former case,one observes asymmetric 3D necklaceshaped wave packets that asymmetric single-layer and multilayer necklace structures in each layer are featured in T-axis,as displayed in bottom row with m=1.5.In addition,we see that the phenomena observed and laws formulated before are still applicable. In a linear medium with a self-consistent trapping potential,we have investigated numerically the dynamics of self-decelerating Airy-Bessel light bullets carrying different TC,exhibiting fundamental zero-TC pulsed structures or non-zero-TC vortices.We have demonstrated that the spatiotemporal profiles can be signi fi cantly changed in induced potential during propagation,which is quite different from that in free space.The appearance of diskshaped fundamental pulses,the necklace rings and the vortex rings results from a combined action of the number of TC,modulation depth and induced potential in the linear medium,all of them acting simultaneously.Our approach may not only prove useful for understanding self-accelerating beams,but also lead to potential applications in signal processing,particle manipulation,and other fields.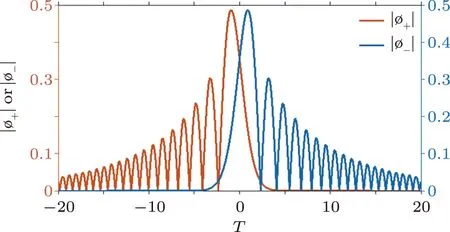
3 Analysis and Discussion
3.1 Zero-Vorticity Airy-Bessel Light Bullets(m=0)
3.2 Vortex Airy Light Bullets(q=1,m=0)
3.3 Necklace Airy-Bessel Light Bullets(q=0,m=0)
4 Conclusion
 Communications in Theoretical Physics2019年6期
Communications in Theoretical Physics2019年6期
- Communications in Theoretical Physics的其它文章
- Efficient Network Dismantling via Node Explosive Percolation∗
- Insights into the Discrepancy between Single Molecule Experiments∗
- effects of Inhibitory Signal on Criticality in Excitatory-Inhibitory Networks∗
- Relativistic Self-Focusing of Hermite-cosine-Gaussian Laser Beam in Collisionless Plasma with Exponential Density Transition
- Study on the Perturbation Characteristics of Two-Channel Laser Propagation in Atmospheric Turbulence
- Dipole and Combo Optical Solitons in Birefringent Fibers in the Presence of Four-Wave Mixing
