航天半硬壳结构模型简化方法研究

赵阳，许博谦，李玉韦

（1.中国科学院长春光学精密机械与物理研究所，长春 130033）

（2.大连理工大学 工程力学系，大连 116024）

随着计算科学技术的日益发展，计算机处理速度和存储能力不断提升，但与此同时工程与科学问题的规模和复杂性也在不断提高，因此，模型简化工作便显得尤为重要。航天工程中的运载火箭全箭精细模型结点数可以达到千万量级，对于其静力学问题，常用的做法是取出较为关心的结构单部段精细模型进行刚度和强度分析，却无法在全箭模型层面上，通过施加某一飞行秒态下的结构载荷来更为真实地获取该部段的受力状态。若针对箭体级间段、箱间段和贮箱等部段的半硬壳结构［1］，提出相应的模型简化方法，便可在此基础上，进一步简化箭体的推进剂、发动机和人造卫星等结构，得到介于传统梁模型和精细模型之间的过渡简化模型，从而利用其进行更为精细的全箭传递路径分析、截面载荷分析和局部强度校核等工作。

在进行静力学模型简化时，通常遵守刚度等效的基本原则。现有针对蒙皮桁条结构的模型简化方法主要为潘忠文［2］和邢誉峰［3］提出的通过对桁条形式进行简化的三种方法，但其存在着扭转刚度误差较大的问题；针对网格加筋结构的模型简化方法主要为张明利［4］提出的将正置等边三角形网格加筋结构简化为各向同性光筒结构的方法，但其也存在着适用面窄的问题。为了解决上述问题，本文对于大直径蒙皮桁条结构，基于潘忠文的梁-壳模型法，进一步提出了采用尺寸优化来修正简化模型扭转刚度的优化定解法；对于网格加筋结构，基于蔡园武［5-7］提出的改进的渐近均匀化思想，提出了将任何具有周期性的网格加筋结构简化为光筒结构的等效性能法。最后，通过算例表明，采用这两种方法得到的简化模型计算精度很高，本文提出的模型简化方法具有很好的工程应用价值。

1 优化定解法

在将蒙皮桁条全壳模型简化为梁-壳模型后，经分析发现梁-壳模型在扭转载荷下无法考虑桁条与蒙皮之间的耦合刚度，梁壳交界区域会出现变形不协调的情况，故导致简化模型出现较大的扭转刚度误差，而在轴向拉压载荷和弯曲载荷下不会出现此种情况，因此本文在进行模型简化时重点关注了梁-壳模型扭转刚度的修正。

1.1 方法介绍

如图1所示，对于沿着周向均匀分布N根轴向桁条的大直径蒙皮桁条结构横截面，假设桁条的截面为圆形，且形心位于蒙皮中面。

此结构在轴向的拉压刚度：

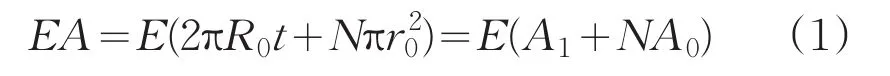
弯曲刚度EIZ（以IZ为例）：

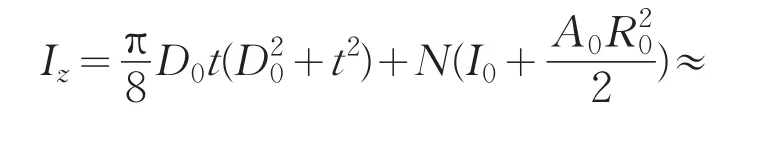
其中，r0为桁条截面半径，R0为蒙皮半径，且有r0≪R0，D0为蒙皮直径，t为蒙皮厚度，A0代表单根桁条的横截面积，A1代表蒙皮的横截面积，E为弹性模量，IZ为截面对z轴的惯性矩，G为切变模量，J为截面对O点的极惯性矩。

图1 蒙皮桁条圆柱壳横截面示意图

由式（1）、式（4）和式（7）可知，蒙皮桁条结构的轴向拉压刚度及弯曲刚度主要由其横截面积决定，而扭转刚度主要由蒙皮厚度决定，因此，在大直径蒙皮桁条结构简化为梁-壳结构后，可采用尺寸优化的方法修正扭转刚度。首先从精细模型中获取横截面积作为约束条件，令简化模型的横截面积与其相等保证轴向拉压刚度和弯曲刚度一致，再通过调整蒙皮厚度使两者的扭转刚度相同，最后取结构局部单胞，令局部弯曲刚度相同，确定简化模型尺寸的最终解。

在优化过程中，利用优化设计软件Isight，采用多岛遗传算法及采用序列二次规划算法混合寻优策略［8-10］，具体的优化流程如图2所示。

图2 尺寸优化流程

1.2 算例验证

建立半径为2456mm，高为2000mm，厚度为3mm的大直径蒙皮，周向均匀分布72根翼板和腹板均长为15mm、厚度为3mm的T形轴向桁条，由于真实运载火箭各部段模型的蒙皮上大多含孔洞，因此，沿周向开了3个边长为550mm的正方形孔洞。材料密度为2.7e-9t/mm3，弹性模E为70Gpa，泊松比μ为0.3。为了考虑梁截面的偏置问题，简化模型采用自定义梁截面，且本算例中桁条根数和分布形式与精细模型一致，具体模型如图3所示。

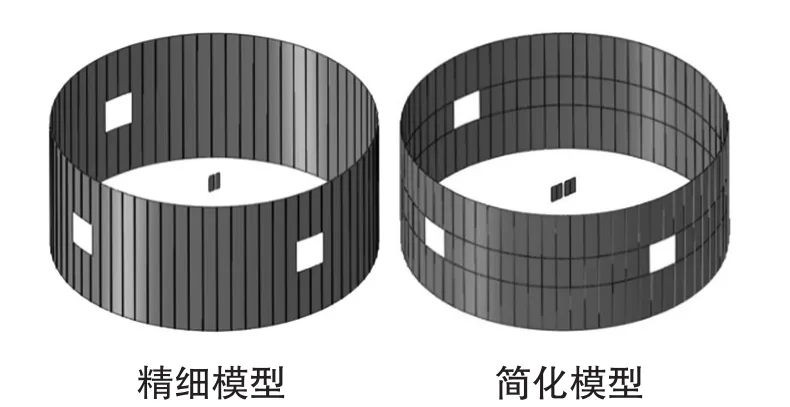
图3 简化前后模型对比

简化前后结构均为底端边界固支，顶端边界和位于圆心处的参考点建立耦合关系，施加2e6N·mm的扭转载荷，并截取结构单胞，在单胞单边中心建立参考点与所在边耦合，对边固支，施加2e3N·mm的局部弯曲载荷，结构整体的轴、弯、扭刚度均通过参考点的位移来表征。

在尺寸优化过程中，由于结构沿轴向的横截面积发生了变化，故应采用分区域优化的方法，即沿轴向将结构分为开口区和未开口区来分别进行优化，此时的优化列式为：

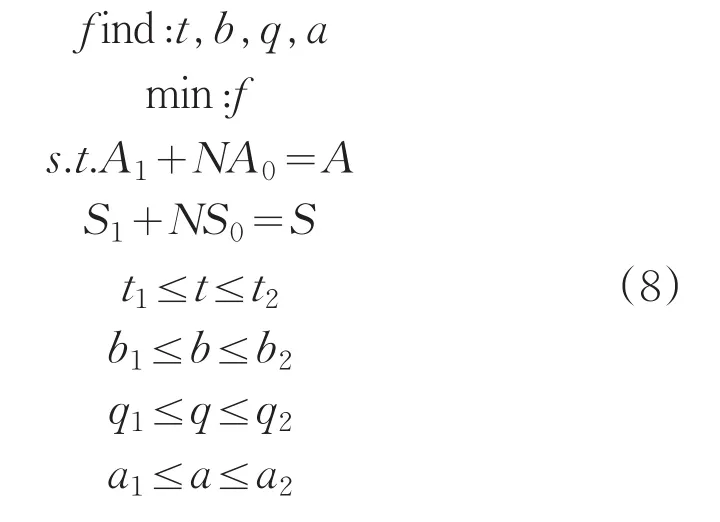
其中，t和q分别为未开口和开口区的蒙皮厚度，b和a分别为未开口和开口区的自定义梁截面边长，f为各个工况下转角差的百分比之和，且f=ju1+ju2+ju3（其中，ju1为扭转工况下的转角差百分比，ju2为未开口区局部弯曲工况下的转角差百分比，ju3为开口区局部弯曲工况下转角差百分比），A1和S1分别为未开口和开口区蒙皮的横截面积，A0和S0分别为未开口和开口区单根桁条的横截面积，A和S分别为精细模型未开口和开口区的横截面积，t1、b1、q1和a1为设计变量的下限，t2、b2、q2和a2为设计变量的上限。

按照优化列式（8）和图2所示的优化流程进行模型简化工作，优化迭代过程及优化结果分别如图4-5和表1-2所示。

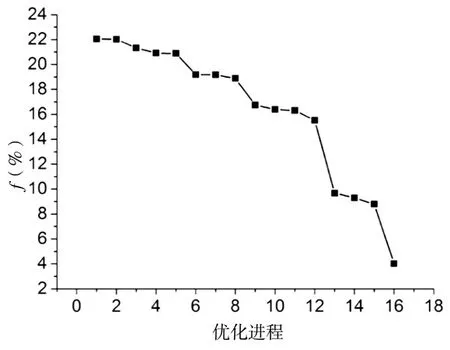
图4 优化迭代曲线

图5 优化迭代曲线

表1 优化结果

表2 优化结果

为验证简化模型的计算精度，对精细模型和简化模型分别施加1e6N的轴压、2e6N·mm的弯曲、2e6N·mm的扭转和2e3N·mm的局部弯曲载荷与相同的边界条件，静力学分析结果如图6-9和表3所示。

图6 轴压载荷下的位移云图对比

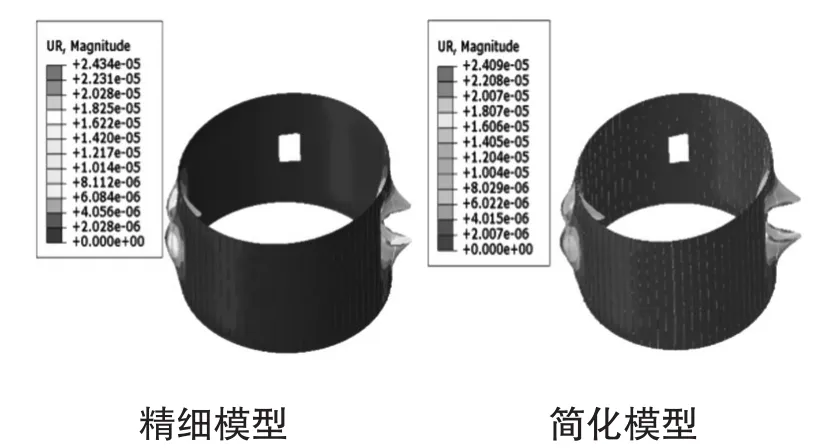
图7 弯曲载荷下的位移云图对比

图8 扭转载荷下的位移云图对比

图9 局部弯曲载荷下的位移云图对比

表3 简化前后位移计算结果对比

由上述可知，简化前后结构在各种工况下的位移云图基本一致，计算误差均小于5%，此结果说明对于大直径蒙皮桁条结构采用优化定解法可得到具有较高计算精度的梁-壳简化模型。

2 等效性能法

针对三维周期性材料和周期性板壳结构等效性质的预测，蔡圆武提出了一种渐进均匀化方法的新求解方法［6］，该方法结合了渐进均匀化方法［11-13］和代表体元法［14-16］的优点，一方面，其具有严格的数学基础，根据摄动理论，结构的等效性质可以通过求解定义于单胞上的偏微分方程组得到；另一方面，其操作简单，可以利用商业软件作为一个黑箱来建立单胞模型并进行分析计算。本文将其应用于周期性网格加筋结构的等效刚度模型简化当中。

2.1 方法介绍

首先，取网格加筋结构单胞并利用商业软件建立有限元模型，对其施加分别等效于三个单位面内应变和三个弯曲应变的节点位移场χ0(λμ)和χ∗(λμ)，对应的载荷向量为：

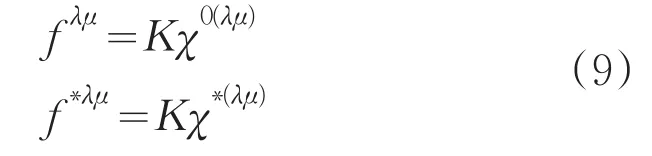
其中，指标λ，μ取值1和2，f为节点反力，K为刚度阵。节点反力可作为静力分析结果从商业软件中输出，进一步将节点力施加在单胞的每个节点上，并在板的面内两个方向施加周期性边界条件，而在上下表面施加自由边界条件，此时，在周期性边界条件下的有限元方程为：

再进行一次静力分析，便可得到节点反力pλμ和p∗λμ，同时间接得到了刚度阵K。最后，由文［6］可知，等效刚度系数可表示为：

其中，指标α，β同样取值1和2，z为沿板厚方向的坐标，尖括号表示在单胞体积上的平均。最后，建立与网格加筋结构精细模型蒙皮尺寸一致的光筒结构并赋予已经得到的结构等效刚度信息，完成模型简化工作，具体简化流程如图10所示。

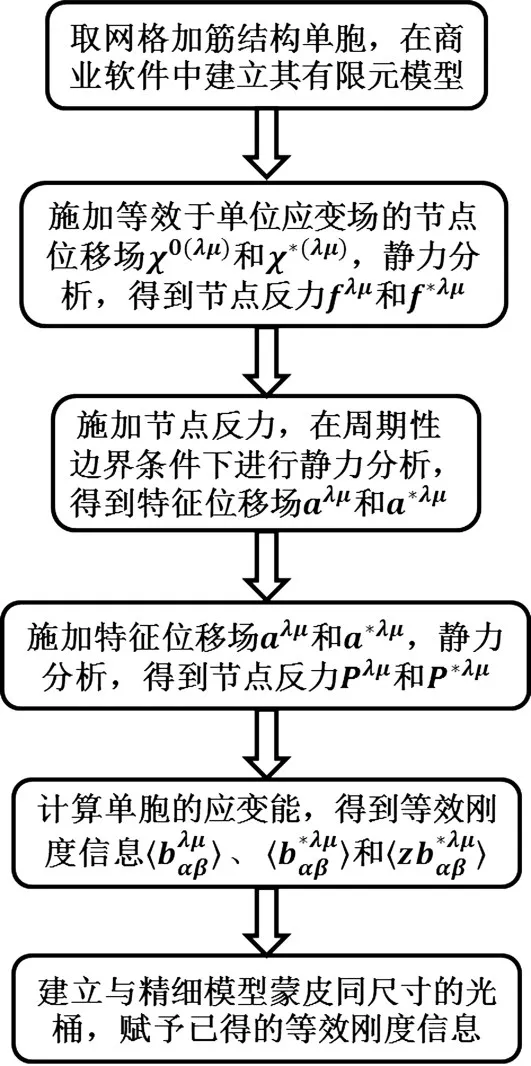
图10 模型简化流程

2.2 算例验证

建立半径500mm，高1178mm，正方形网格边长130mm，筋条高10mm的网格加筋结构，蒙皮和筋条的厚度均为1mm，材料密度为2.7e-9t/mm3，弹性模量为210Gpa，泊松比为0.3，简化模型为与精细模型蒙皮同尺寸的光筒结构，具体模型如图11所示。

图11 简化前后模型对比

图12 正置正交网格加筋结构单胞

取如图12所示的结构单胞，并按照图10所示的操作流程进行模型简化工作，得到的等效拉伸刚度[A] 、耦合刚度[B]和弯曲刚度[D]如下：

为了检验光筒简化模型的计算精度，在精细模型和简化模型的顶端圆心处建立参考点并与顶端边界耦合，将底端边界固支，对其分别施加1e6N的轴压、1e6N·mm的弯曲和1e6N·mm的扭转载荷，结构整体的轴、弯、扭刚度同样均通过参考点的位移来表征，静力分析结果如图13-图15和表4所示。

图13 轴压载荷下的位移云图对比

图14 弯曲载荷下的位移云图对比

图15 扭转载荷下的位移云图对比

表4 简化前后位移计算结果对比

由以上结果可知，简化前后结构在各种工况下的位移云图基本一致，计算误差均小于5%，说明对于正置正交网格加筋结构采用等效性能法可得到具有较高计算精度的光筒简化模型。

3 结论

本文基于刚度等效的原则，对航天半硬壳结构的模型简化提出了优化定解法和等效性能法，两种方法均具有清晰的理论基础且操作简单。

（1）优化定解法一般适用于具有大直径的蒙皮桁条结构，可以将其简化为梁-壳结构，在结构形式得到简化的同时，简化模型与精细模型之间的刚度误差小于5%。

（2）等效性能法适用于具有周期性的网格加筋结构，可将其简化为光筒结构，在结构形式得到简化的同时，简化模型与精细模型之间的刚度误差也小于5%。

相应的算例验证了两种模型简化方法的有效性，同时也说明了本文提出的模型简化方法具有很好的工程应用前景。