基于灰关联度理论降雨不同非饱和参数边坡的渗透稳定性分析
宋亚萌,雷锋国,王成华
(1 天津大学建筑工程学院,天津 300350;2 中铁十八局集团有限公司,天津 300350)
降雨是影响边坡稳定的重要因素[1-4],降雨会使得边坡内部水位变化[5-6],土体强度参数降低[7-8]以及渗流力指向坝坡外部[9],从而加剧下滑趋势,导致坝坡失稳。对于降雨导致边坡失稳的例子有很多,如1963年意大利Vajoint水库[10]在降雨时发生了大规模的滑坡事件降雨导致的边坡失稳会对边坡周围的居民生命、财产造成威胁,以及周边的建筑物形成永久的损坏,因此,对降雨条件下的边坡渗透稳定性的研究意义重大。
对于降雨条件下的边坡稳定性分析,国内外许多学者进行了大量有益的研究,杨攀[11]对前期降雨条件对边坡渗透稳定性进行了数值模拟分析,顾成壮[12]分析了强降雨饱和状态下四川汉源二蛮山滑坡的临界失稳状态,郭爱斌[13]对淹锅沙坝滑坡在降雨入渗下的安全系数变化进行了分析,但是以上研究均未考虑到土体的非饱和程度对于降雨条件下边坡渗透稳定性的影响。事实上土体的非饱和参数(通常是以VG模型或者是Fredlund&Xing模型刻画)对于边坡的非饱和渗透稳定性的影响巨大,如张磊[14]分析了不同非饱和参数对于降雨边坡的影响程度,郁舒阳[15]基于Fredlund & Xing参数对降雨条件下的不同非饱和参数对边坡渗流特性以及边坡的安全系数变化进行了数值模拟,但是以上研究均未进行非饱和参数的定量化敏感性分析。
本文研究以文献[15]的算例为例,基于灰关联度理论对降雨条件下不同Fredlund & Xing参数对边坡渗透稳定性的影响进行定量化敏感性分析,研究成果可为认识非饱和参数对边坡影响的规律提供一定的参考。
1 计算理论
1.1 非饱和理论
非饱和渗流的控制方程形式为:
(1)
上式中:kr为相对透水率,kij为饱和渗透张量,hc为压力水头,Q为源汇,C(hc)为容水度,θ为压力水头函数,n为孔隙率,Ss为单位贮水量。
1.2 Fredlund & Xing非饱和模型[16]
土水特征曲线是衡量土体内部渗透系数(体积含水量)与基质吸力之间的关系,比较广泛使用的是Fredlund & Xing模型,其控制方程如下:
(2)
式(2)中:θw为土体的体积含水量;C为函数的修正函数,根据文献[15]的建议,本文取为1;θs为土体的饱和体积含水量;e为自然对数,其值为2.71828;Φ为负孔隙水压力;a、m、n为拟合参数,a是体积含水量的拐点,其值略大于进气值,单位为kPa,m控制了残余含水量,n控制了体积含水量函数的斜率,表达形式如下:
a=φi,
(3)
(4)
(5)
式(3)~(5)中:Φi为曲线拐点对应的基质吸力,s为拐点处的斜率。
而土体的渗透系数函数如下:
(6)
式(6)中:kw为含水量或者负的孔隙水压力计算所得的渗透系数,ks为边坡土的饱和渗透系数;y代表负孔隙水压力算法的虚拟变量,i为j到N之间的数值间距;j为最终函数所描述的最小负孔隙水压力,N为最终函数所描述的最大负孔隙水压力,Ψ对应于第j步的负孔隙水压力;θ0为方程的起始值。
1.3 非饱和抗剪强度理论
本文采用Fredlund双应力变量公式[16]
s=c′+σntanφ′+(ua-uw)tanφb,
(7)
式(7)中:c′与φ′为有效强度参数,σn为法向总应力与孔隙气压力的差值,ua为孔隙空气压力,uw为孔隙水压力,φb表征由负孔隙水压力而提高的强度。
1.4 灰关联度理论
灰关联度[17]属于灰色系统理论,可以在相对有限的资料下较为准确的找到影响因素值与目标影响值的联系,关联度的大小与比较因素和参考因素的相关性成正比,具体步骤如下:
1.4.1 确定比较矩阵与参考矩阵
对于Hoek-Brown准则,可以选取反映土体非饱和程度的a、m、n、k参数等为比较矩阵,即
(8)
将边坡的安全系数作为参考矩阵:
(9)
1.4.2 矩阵的无量纲化
为了消除各个参数之间的差异性,及方便进行比较,对1.2.1节所述的比较矩阵和参考矩阵进行归一化处理,比较矩阵为
Xi′=[Xi′(1),Xi′(2),…Xi′(n)],
(10)
式(10)中
(11)
同理,参考矩阵为
Yi′=[Yi′(1),Yi′(2),…Yi′(n)],
(12)
式(12)中:
(13)
1.4.3 确定灰关联差异信息空间
对比较矩阵和参考矩阵进行差异性分析,计算其差异矩阵:
Δij=|Yi′(j)-Xi′(j)|,
(14)
取其最大最小值:
Δmax=max(Δij),
(15)
Δmin=min(Δij)。
(16)
1.4.4 计算灰关联度系数矩阵与灰关联度
关联系数可以根据下式求得:
(17)
式(17)中:μ为分辨系数,范围为[0,1],本文取为0.5。
关联系数矩阵内数据较多,比较不同因素的影响程度较为困难,因此求出每个因素关联系数的平均值作为关联度,即
(18)
关联度Di值在[0,1]变动,Di值越大,代表影响因素的关联度越大,即敏感性越大。
2 计算模型
2.1 计算模型及边界
计算模型选择文献[15]中的计算模型,如图1所示,设置上部与下部监测点来实时监测边坡内部不同点的孔压变化。边坡高度hf=14 m,坡脚高度ac=7 m,坡比为1∶2,初始条件为图1所示的初始水位线计算所得的初始渗流场作为整个计算模型的初始条件,边界条件设置如下:cdef为降雨入渗边界;cb、gf、ah为不透水边界,ab、gh为定水头边界,分别为3 m与8m。模型网格图如图2所示,整个模型共划分为1847个节点,1752个单元。
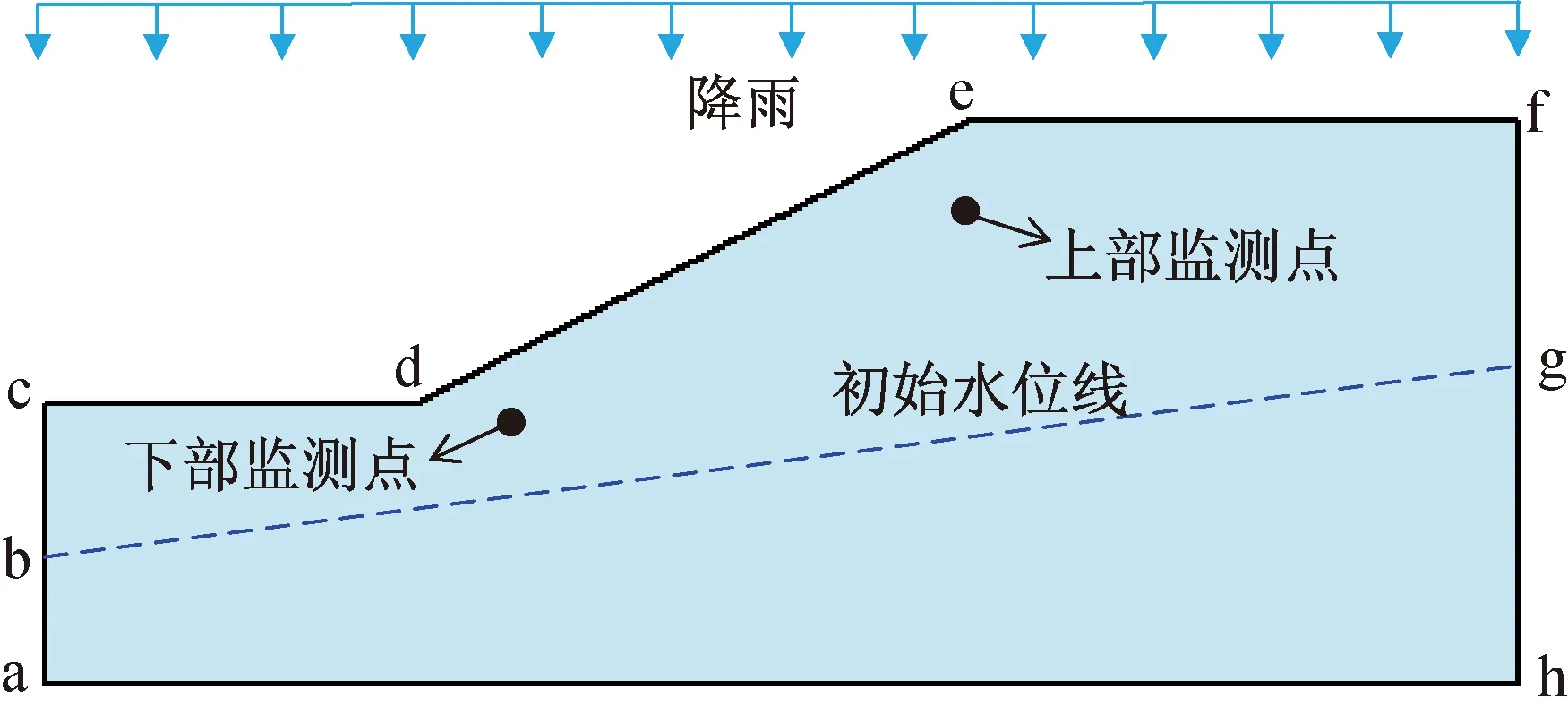
图1 计算模型Fig.1 Computational model
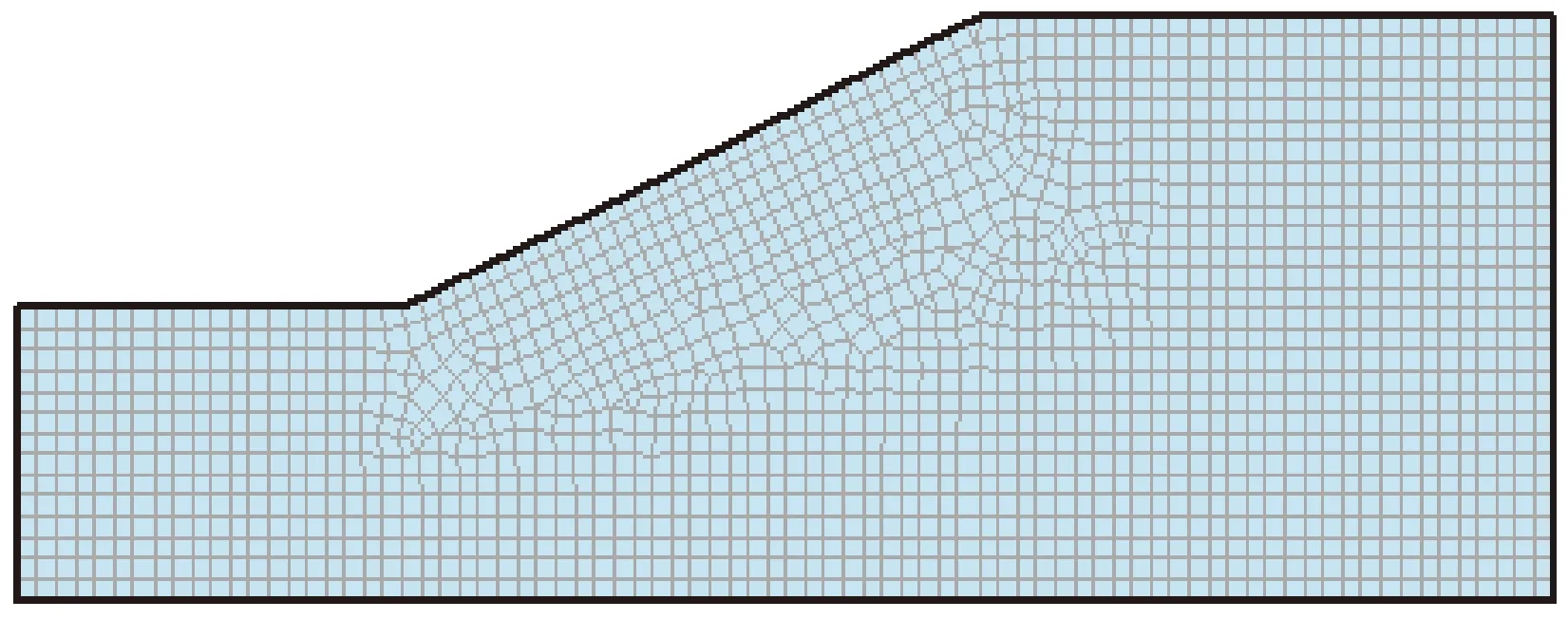
图2 模型网格Fig.2 Model mesh
2.2 计算参数及计算工况
材料的基础参数根据文献[15]取值,饱和体积含水量θs为0.1 m3/m3,重度γ为18.6 kN/m3,黏聚力c为22 kPa,内摩擦角φ为16°,φb为20°。非饱和参数a、m、n、k基础参数取为a=10 kPa,m=1,n=4,k=0.01 m/d,相应的计算工况为改变土体非饱和参数k、a、m、n,计算边坡的渗透稳定性,降雨强度取为0.01 m/d,降雨持续时间取为10 d,考虑停雨10 d的情况,相应工况如表1所示。

表1 计算工况Tab.1 calculation conditions
3 计算结果与分析
3.1 渗流场分析
不同工况下不同监测点(上部监测点与下部监测点)的孔压变化规律如图3、图4所示。
由图3、图4可知,上部和下部监测点以及不同工况下的孔压变化规律大不相同,总结可以发现以下规律:
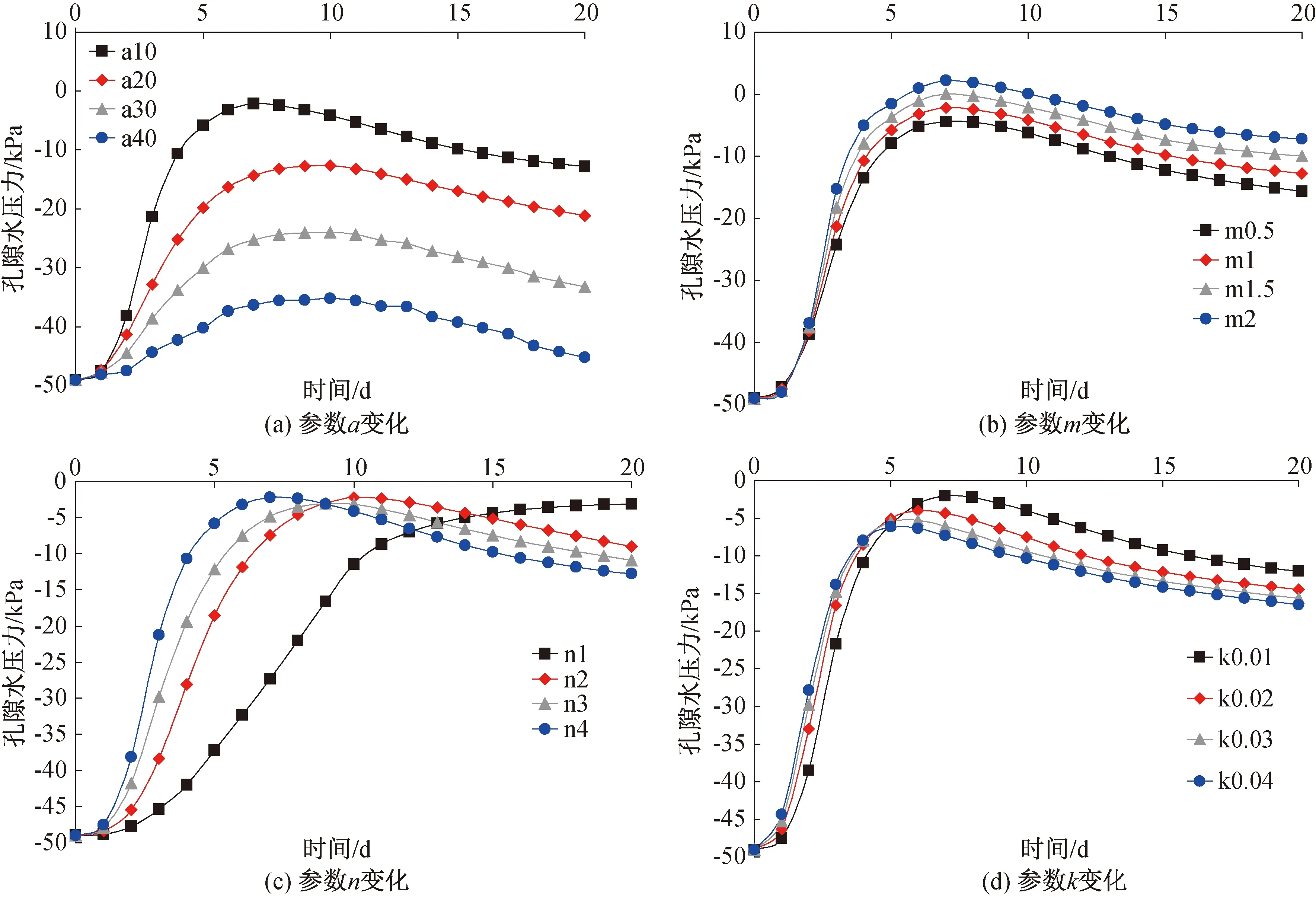
图3 上部监测点孔压的变化Fig.3 variation of pore pressure at upper monitoring points

图4 下部监测点孔压的变化Fig.4 change of pore pressure at the lower monitoring point
(1)总体上而言,上部和下部监测点的孔压都随时间呈现在降雨时迅速增大,而在降雨结束时刻缓慢减小的趋势。
(2)对于上部监测点,参数a、m和孔压上升的幅度呈正相关,而参数n与k越大,在降雨时上升越快,在降雨结束后下降也越快。
(3)对于下部监测点来说,参数m、n与孔压上升的幅度呈正相关,参数a越大,孔压增幅缺越小,但是在参数a=40 kPa时却有一个突然的上升,参数k越大,前期孔压上升幅度也越大,而在降雨结束后孔压下降也越快。
(4)对于同一工况来说,下部监测点的孔压整体上要大于上部监测点的孔压。
3.2 边坡稳定性分析
不同工况下的边坡安全系数的变化规律如图5所示。由图5可见:
(1)不同工况下的安全系数呈现在降雨时迅速下降、停雨后缓慢下降的趋势。
(2)参数a越大,整体安全系数也越大,但是当a=40 kPa时整体安全系数有一个突然的陡降;参数m、n、k越大,安全系数整体上也越大。
(3)参数k在降雨前期安全系数几乎一致,而在降雨后期安全系数则随着渗透系数k的增大而减小。

图5 安全系数的变化Fig.5 Law of variation of safety factor
4 灰关联度敏感性分析
为定量化研究不同工况下安全系数对非饱和参数敏感性的影响,取不同工况下的非饱和参数作为比较值,并取边坡在降雨过程中最小安全系数作为参考值,不同工况下最小安全系数见表2。
由表2所列的最小安全系数,按式(8)、(9)构建比较矩阵为:
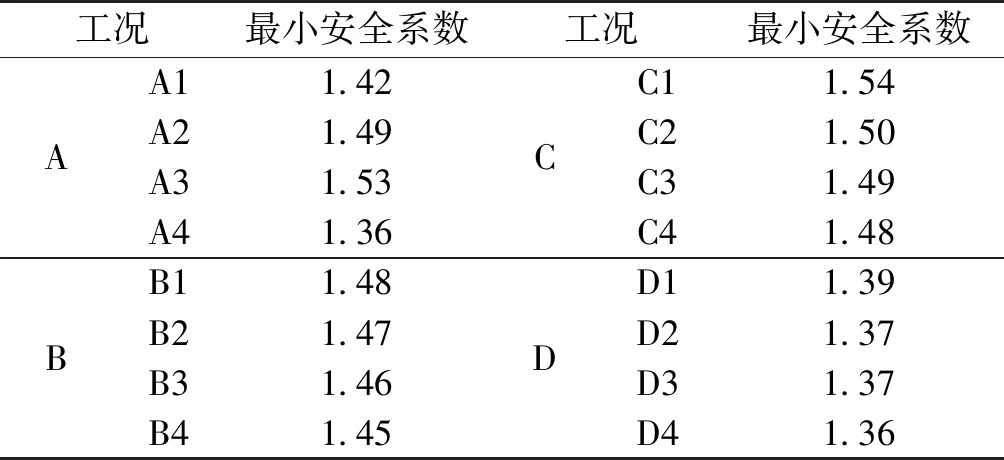
表2 最小安全系数汇总Tab.2 Summary of minimum safety factor
(19)
参考矩阵则可以表示为:
(20)
根据式(19)、(20)可以得到相应的差异矩阵为:
(21)
灰关联系数矩阵式为:
(22)
最后得到关联度D为:
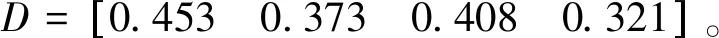
(23)
由此可以得到灰关联度敏感性大小排序为a>n>m>k。
5 结论
(1)降雨条件下上部、下部监测点的孔压都随时间呈现在降雨时迅速增大、在降雨后缓慢减小的趋势;对于同一工况,整体上下部监测点的孔压要大于上部监测点的孔压。
(2)边坡安全系数在降雨时迅速下降,而停雨后缓慢下降,参数a越大,整体安全系数越大,但在a=40 kPa时整体安全系数有一个突然的陡降;参数m、n、k越大,整体上安全系数也越大。
(3)降雨条件下参数a与参数n对边坡的渗透稳定性影响相对较大,而参数n与参数k影响则相对较小。

