基于浴盆曲线的整车耐久试验故障曲线

陈伟波，范 韬，叶 欣，刘文彬，袁 涌

(泛亚汽车技术中心有限公司 试验认证部,上海 200120)

整车耐久试验是一种模拟客户使用的整车级加速试验，是代表客户评价整车可靠性的重要方法，同时也是考核和评价汽车质量的最终技术措施和手段，是整车设计认证的最后一道关口[1-3]。整车的可靠性需要科学的评价指标来指导与评价耐久试验的结果。目前关于整车耐久试验的评价方法有很多，比如通过概率和数理统计方法将故障数据(如里程信息)作为随机变量进行分布函数拟合和优化，寻出最优的分布函数[4]，这种方法可以较好地评估产品的可靠性水平。或基于某种模型，对耐久试验的总故障数进行预测[5]，这种方法更多是关注累积统计，进而来评估项目质量风险。但是实际应用中，故障数据有时是随机的，可能不服从某种分布或置信度较低。而且如果只针对故障总数有要求，不对每段时刻的故障数设置指标，会提高监控的风险性。

为此，笔者基于浴盆曲线理论，结合整车耐久试验模拟客户使用的前期质量和长期可靠性，利用盒须图方法处理大量实际试验数据，针对试验里程建立一种新的整车耐久试验故障分布指标和评价方法。

1 浴盆曲线理论

整车质量中的前期质量，或者说客户对于新车的感知质量，越来越得到市场的重视，是在客户驾驶或乘坐车辆的过程中，通过看、听、闻、触等主观感受，所获得的车辆在外观、内装、便利空间、整车性能等方面的直接评价[6]。JD.Power公司针对感知质量有很多调查方法，其中IQS(initial quality survey)新车质量调查，是一种比较重要的方法，其调查了客户在2～6个月的客户新车使用的抱怨度。2018年JD.Power公司发布了主流车的IQS数据，如图1所示，PP100为每百辆车问题数，分数越低，表明问题越少，质量越好。目前主流车企已经越来越重视新车质量，基本都高于市场平均水平。

图1 2018年主流车IQS数据(JD.Power)

图2 客户使用故障分布曲线

传统上，整车耐久道路试验更加注重中后期质量，考察各零件在长期载荷积累的情况下是否能够不发生失效，但现在车辆的前期质量越来越被消费者看重。客户使用故障分布曲线如图2所示，可知体现整车耐久试验的指标需要将车辆的客户前期质量评价与长期可靠性结合起来，对耐久试验的全过程进行监控。其中，故障曲线A表示初始性能或功能不满足客户期望；故障曲线B表示制造或安装问题；故障曲线C表示设计不满足强度(环境/使用)要求；TOTAL表示总体故障问题。整车耐久试验模拟了客户的整个生命周期的考核要求，对于故障曲线A、B、C都应该涵盖，故障数总体应该呈现：在客户使用初期主要感知质量和制造安装问题，在使用中后期主要关注耐久性的强度问题。这个故障发生的区域，总体曲线满足浴盆曲线理论。

浴盆曲线如图3所示。故障随使用时间变化分为初始故障期、偶发故障期和耗损故障期3个阶段[7]。对于整车耐久试验来说，在试验初期，由于各种制造安装问题和客户感知质量问题，故障数开始较高，随后迅速降低；在试验中期，故障数因为随机故障而进入稳定期；在试验后期，零件在载荷的累积下不断失效，整车故障数不断升高。

图3 浴盆曲线图

2 耐久试验数据分析

为了得到历史故障数据的分布曲线，需要对试验故障数据的故障里程进行分析。由于整车耐久试验过程中，车辆发生失效后是可修复的。对于可修复系统，由于在发生故障后仍可继续使用，所以实际上人们最感兴趣的是无故障工作时间的平均值，常用MTBF(平均故障间隔时间)来表征，指产品或系统在两相邻故障间隔期内正确工作的平均时间，是标志产品或系统能平均工作多长时间的量[8]，其计算式为：

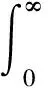
为了表示浴盆曲线中每一阶段的故障数，需要知道每一阶段的MTBF，设将总时间为T的整车耐久试验分割为n份，在每一份的MTBFi的表达式为：

其中，i=0,1,…,n-1。

根据故障数的计算式，将历史故障数据按照10%的故障数进行统计，并按照不同的项目更改类型和车辆造车阶段进行分类，得到的故障率分布曲线如图4所示。

图4 故障率分布曲线

项目更改1～项目更改4按照项目改款大小依次是由大到小，造车阶段1～造车阶段4按照接近量产车状态依次是由远到近。由图4可知，不论是按照项目更改统计，还是按照造车阶段统计，故障数按照试验进度的走势基本与浴盆曲线的走势一致，并且按照项目更改和造车阶段，故障数在各个试验进度下逐渐降低。

3 整车耐久试验评价指标

从上述分析可得到实车的故障分布曲线，但是如何根据实车数据的状态进行评价，需要一个评价指标来衡量实际曲线的表现。

传统的计算方法需要知道历史试验数据的分布情况，如是否符合正态分布或韦布尔分布，但是在处理实际数据的过程中，并不是每一个检查时刻点的历史数据都服从某种分布，或者不是所有数据都服从同一种分布，例如图5所示的SOT(0%)试验故障样本分布，可知0%的SOT检查的样本数据，通常是用某种分布曲线去拟合数据，然后取一定百分比的上下限。但该数据分布较为分散，每10%的数据分布可能完全不同，所以如何剔除异常值，确定这些数据的上限与下限，需要更加稳健的方法。

图5 SOT(0%)试验故障样本分布

3.1 盒须图理论

引入稳健统计学的盒须图理论，可以真实客观地表现数据形状的本来面貌。盒须图的绘制依靠实际数据，不需要事先假定数据服从特定的分布形式，没有对数据作任何限制性要求，能够根据数据本身的特点来识别背景总体和异常总体，提供数据变化范围和极端值的信息[9-10]。

盒须图引入了一个简单明了的图示技术，是一种表现最小和最大观测值以及第1、第2、第3个四分位数的图形方法。在盒须图上，可以表现第1个四分位数(Q1)、中位数(Q2)、第3个四分位数(Q3)以及四分位数间距(IQR=Q3-Q1)[11]。Q3+1.5 倍IQR和Q1-1.5倍IQR分别为上下限；处于上下限以外位置的点表示的数据均为异常值。盒须图关键参数的计算方法如表1所示。

将盒须图理论应用在SOT故障分析上，以图5的样本为例，得出中位数是9，上四分位是15，下四分位是4，因此IQR=9。按照表1中上下限计算公式，上、下限分别为min(31.5，35)和max(-12.5，1)，考虑实际情况并取整得上限为31，下限为1。故原始样本中的35确定为异常值，需要剔除。盒须图取值方法如图6所示，可知参考上限定为31，参考下限定为1，说明大多数历史数据都分布在1到31之间。

表1 盒须图关键参数的计算方法

图6 盒须图取值方法图示

3.2 参考线确定方法

首先搜集所有故障数据，提取故障进度信息，然后按照项目更改1～项目更改4和车辆阶段1～车辆阶段4进行分类，可分为16类，统计出所有项目故障在各个百分比的故障分布图，如图7(a)所示。对于每一类进行10%间隔统计，得出每10%的故障分段统计图,如图7(b)所示。基于盒须图理论分段做出盒须图，连接每个阶段的上限点与下限点，最后圆整数据，得出每一类的上限参考指标和下限参考指标，某分类车辆各阶段问题数盒须图如图8所示。每一条上下参考指标区域代表的是历史数据中依据盒须图理论剔除掉异常值的绝大多数数据的分布区域。

图7 各阶段故障分布

图8 某分类车辆各阶段问题数盒须图

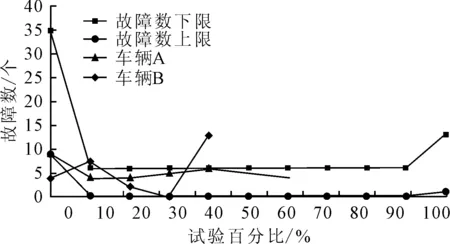
图9 评价结果

3.3 针对故障分布曲线的评价方法

结合某项目浴盆曲线故障数统计，评价结果如图9所示，车辆A在60%的耐久试验过程中，整体曲线都在上下限之间，且没有较大的突变(突然变大或者突然变小)，该车的故障数走势与参考线一致，说明该车不论在初始质量的检查上，还是在后面各个阶段的检查都满足了要求。车辆B在0%处的初始检查低于下限，说明该值比历史数据的下限还低，提示需要进一步检查，而如果忽略该值，后续10%的检查位置很大概率上会突升；在40%点上，相对于30%节点的数据有明显的突升，此时，需要对每一个问题进行分析，看是否有提前发现的可能性，降低在试验中后期发现SOT问题的概率。

综上，可得出利用该故障分布曲线的策略：①在耐久试验早期，加强基于客户使用的各种场景类的SOT检查，让早期失效提前暴露，满足浴盆曲线第一阶段的趋势；②在耐久试验中后期，若某10%阶段的问题数量“突降”，此时提示检查人员应该着重检查车辆，否则应该在此阶段发现的试验故障会延后堆积；③在耐久试验中后期，若某10%阶段的问题数量“突升”，则对每一个问题发生的条件进行分析，是否有提前发现的可能性。总之，应使得故障分布曲线按照参考曲线的趋势暴露，尽量让故障数平稳出现，避免故障数突变。

4 结论

笔者基于浴盆曲线的理论，将盒须图与整车耐久道路试验评价相结合，总结出基于浴盆曲线的整车耐久试验故障曲线评价方法，可以有效地应用于整车道路试验和整车开发工作中，同时也可以应用于产品前期、中期和长期的可靠性评价。

(1)根据稳定性统计学的盒须图理论和历史数据，确定了各阶段整车路试可靠性评价故障数的上下限，低于故障数下限时，则需加大试验评估频次和强度，高于故障数上限时，则需分析故障较多的原因，评估项目风险。

(2)利用该曲线可以描述整个生命周期故障分布情况，且可以参照参考曲线，结合故障原因，分析整车制造能力、零部件认证能力、零部件工艺生产等。

(3)通过不断的数据积累，总结整车开发项目质量评价标准，应用于后续不同阶段、项目、车型等工程开发工作，以便对其进行有效的质量管控和风险评估。