一种基于陆基导航的测速测距方法

廖延娜, 商语秋

(西安邮电大学 理学院， 陕西 西安 710121)

陆基导航是以地面无线导航站为参考，对飞行器进行定位和导航的。相比于卫星定位系统，陆基导航系统成本低廉，维护保养方便，保密性好，抗干扰能力强，所以已成为一种重要的飞行器导航方式[1-3]。在卫星导航遭到干扰，卫星星历不足时，陆基导航是一种重要的补充方式，可以解决特殊时期空中飞行器的导航问题。而飞行器的主要特点就是高速飞行，从亚音速的航空飞行器，到7～8马赫飞行的其他飞行器。其速度引起的多普勒频移，是该类导航系统中必须处理的核心问题之一[4-6]。

在导航接收机方面，无线导航目前往往是和其他诸如惯性导航等方式进行组合导航的[7]。因此，陆基导航往往只测量飞行物到地面站的距离，进而定位，将位置信息传输给导航系统。用来进行多普勒处理的速度信息往往来自于惯性导航系统[8-10]。

当一个飞行器本身没有惯性导航系统，或者要进行独立无线导航的时候，除了测距，测速也就会成为该无线导航的一个任务。由于布站的原因，也会引起几何精度因子(geometric dilution of precision， GDOP)值的变化，水平位置精度因子(horizontal dilution of precision，HDOP)值是GDOP值的水平分量，陆基导航系统中地基站的几何分布与定位精度之间关系的参考值[2]。HDOP值越小，定位精度就越高[3-4]，所以，合理布置基站，是陆基导航定位系统设计中关键的一环[4-6]。本文拟研究在独立的无线导航系统中，利用时间和空间的信息，进行测速的方法。

本文重点在于测速方法的研究，没有在几何因子方面去做考虑。因此，在飞行器飞行末端，由于飞行器远离布站区域，而使得整个导航系统的GDOP值变差，从而导致测速精度的下降，这也是陆基导航本身的一个缺陷。同时，导航区域受限，也是陆基导航本身的特点[8]。

1 陆基导航原理

考虑地面上布置3个以上的地面站，飞行器向地面站发送测距信号，地面站收到后立即反发出来，再被飞行器上的接收机接收。飞行器收到的信号进行时延计算，从而测出到第i个地面站的距离Li。地面站位置坐标Gi(xi,yi,zi)已知，则飞行物本身位置(x,y,z)和飞行物到第Li个地面站的距离 可表示为

(1)

若考虑用3个地面站对飞行器进行测距，式(1)中i=1,2,3。当进行测距完成后，即xi、yi、zi和Li已知，所以，利用式(1)可以建立方程组如下

(2)

通过求解方程组(2)，能够解算出飞行物的具体坐标。

一般情况下，伪码测距的数据包括整数和小数两个组成部分，整数部分可以理解为整数伪码周期及整数个伪码码片的部分，整数部分容易的获得。小数部分则指示小于一个伪码码片的伪距部分，直接反映了测距精度[2]。

从飞行器上天线发出信号到接收到信号之间的时间间隔为ti，飞行器上收发处理机和地面站内部传输总延时为tid，则，Li=C(ti-tid)，其中C是光速。在具体的数字信号处理中，考虑到测距码的帧周期往往远小于tid，因此，为了精确测量，在测量tid的时，除计算整帧周期的倍数时间外，还应该进行剩余时间的测量。用相关峰匹配可以进行整周期外的时间的测量，这样就可以把测距误差控制在半个码元宽度。比如测距码帧长2 ms，如果测距码码长为2 048 bits，测量误差就是0.5 ns，相当的测距误差就是15 cm。如果在相关峰匹配时，不是按照整个码元宽度移位进行匹配，而是以小于码元宽度进行移位，这样就可以进一步提高定位精度。

2 测速原理

由于飞行物的高速飞行，不可避免的会有多普勒频移，多普勒频移的处理依赖于对速度的测量。频偏估计的方法可以在一定程度上去估算多普勒频移，但是造成的误差乃至造成的系统接收灵敏度的降低对系统是指标一个损失。

飞行物上一般用速度计、加速度计等惯性器件测速，但是，在没有惯性器件的时候，就可以应用本无线测速。在定位的时，飞行器发出定位码，地面站接收后就发回。也就是说，几个地面站同时进行测距。

采用每一次对一个地面站发送测距码的方法，然后在一个很短的间隔(几个毫秒)后，再对第二个地面站发送测距码测距，以此类推。完成3次测距，就可以进行位置的计算。假设3次测距时的位置分别为P1、P2、P3，如图1所示。

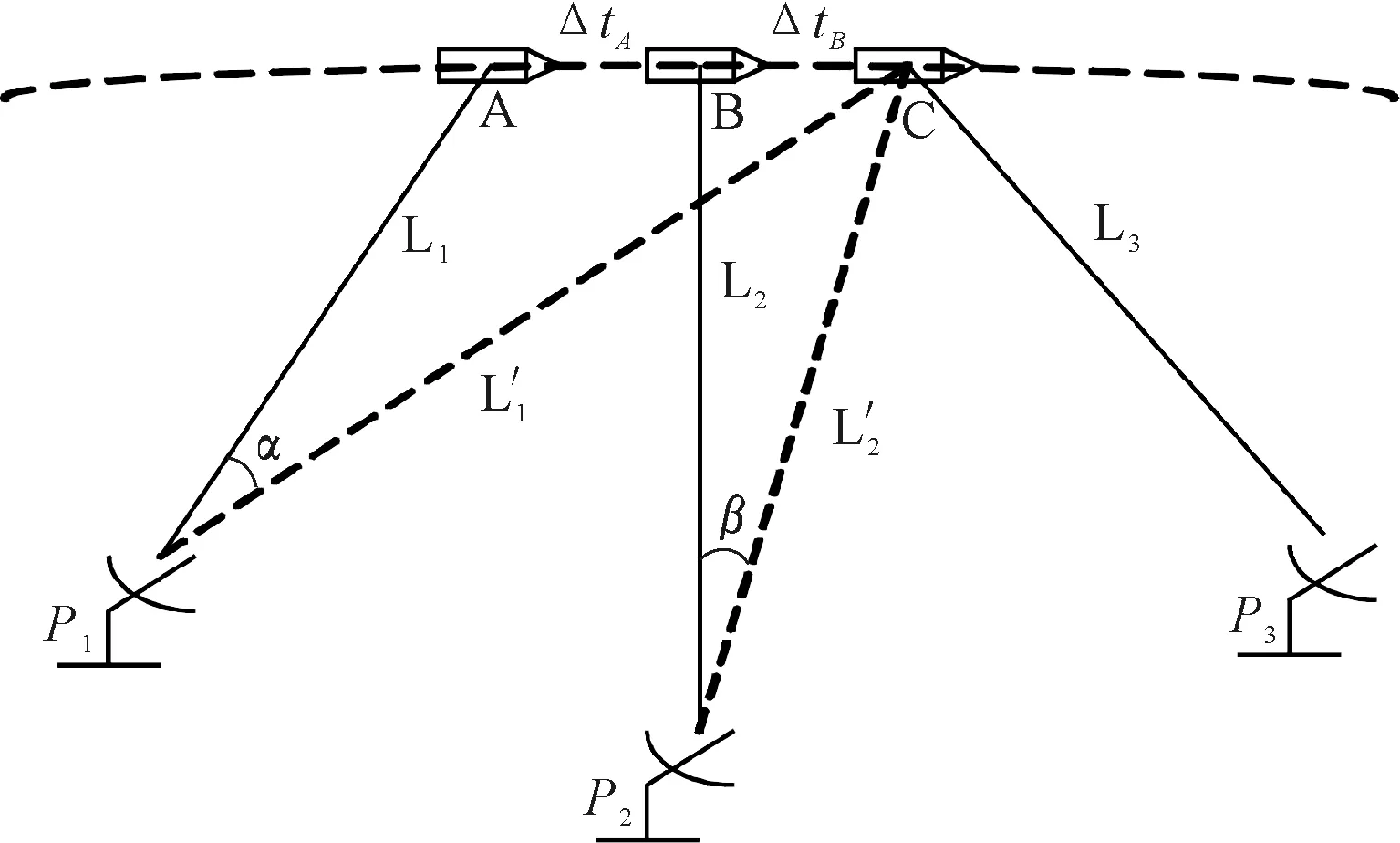
图1 3次测距时的位置示意图

速度的计算则需要定期(约100～200毫秒)地进行测距定位，利用两次定位的结果就可以计算出飞行物的速度。

通常情况下，飞行物虽然速度大小时常会较大且会发生变化，但是，其速度值在飞行过程中应该都是连续变量。如果把间隔时间设置成毫秒数量级，每次测距位置的变化量不可以忽略。例如，当飞行器的速度为200米/秒时，每5毫秒对应距离的变化量达到1米，本身加上测距的误差在±0.5米以内，这会造成测速的误差的增大。所以，必须对测距进行修正。

假设间隔几个毫秒测一次距的时，将飞行器速度看成匀速运动。即在3次测距时，两个时间间隔内，飞行器其速度为v=(vx,vy,vz)。令飞行物从A点飞到C点的时间为ΔtA；从B点飞到C点的时间为ΔtB。则在C点的飞行器对目标位置修正的估计结果为

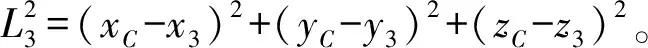
(3)

其中L′1和L′2为飞行物运行到C点时与1和2站之间的距离，此距离需要通过下面的方程组来求解得到。设∠P1AC=α,∠P2BC=β,则该方程为

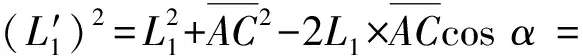
(4)

(5)

这样，两次测量就会得到类似于式(3)的两组方程。通过解两组6个方程，就能得到(x,y,z)和(vx,vy,vz)。

3 仿真结果

3.1 仿真条件

仿真条件参数设置分别为目标的起始坐标为(0,0,0)处，地面站位置坐标分别位于A(-13 000 m, 10 000 m, 50 m), B(-20 000 m, 0 m, 0 m), C(-6 000 m, 10 000 m, 200 m)。

飞行物发射3个测距时刻为(0 s，0.004 s，0.01 s)，测速周期0.14 s。飞行器实际轨迹和实际速度结果如图2所示。

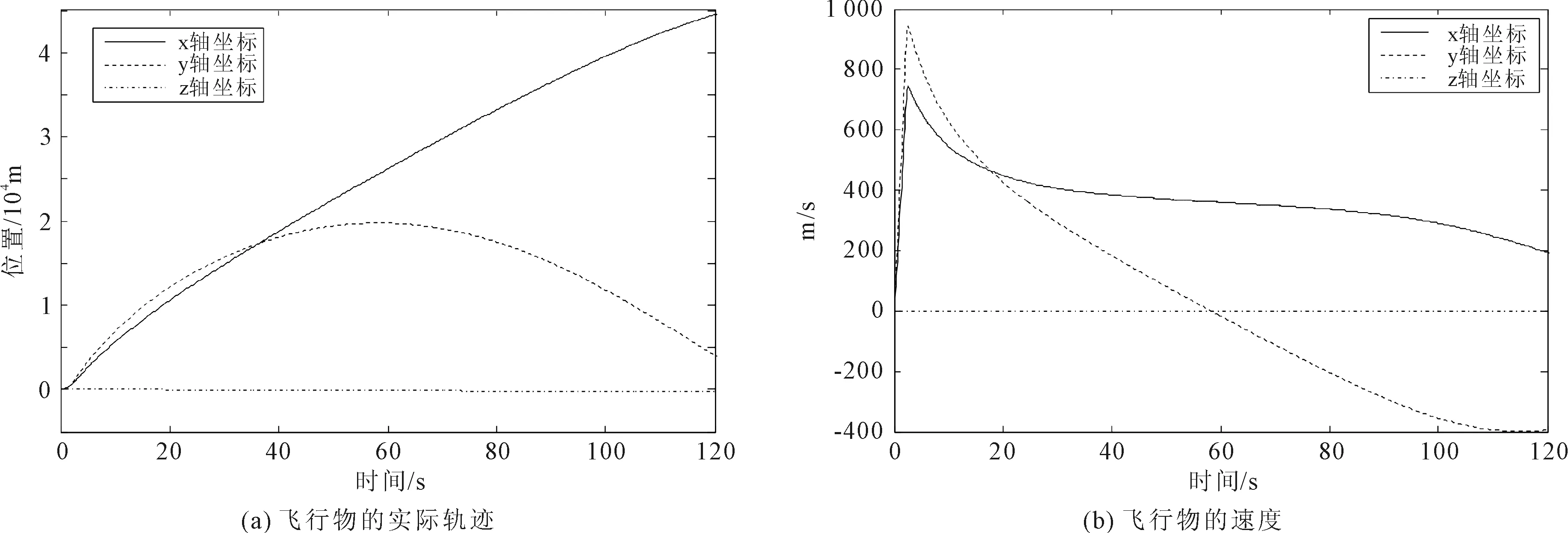
图2 飞行物的实际参数

3.2 仿真结果

为了验证本文方法的有效性，采用在给定一条飞行器实际的弹道上进行仿真验证。仿真了未修正前和利用本文方法修正后的计算结果与实际弹道、弹速的差，其结果如图3所示。

从图3可以看出，修正后的算法在飞行中段定位和测速的精度都优于未校正算法。所以，式(3)和式(4)对位置变化引起的飞行器到地面站之间距离的修正是很有必要的。在20秒到100秒的飞行中段内。修正后的测距精度为定位误差不大于10米，中段修正后测速误差不大于20米/秒。在飞行初段，由于加速度过大，导致速度变化过快。而在飞行末段，由于飞行器距离远离地面站分布区域而导致几何因子的下降，所以该段的定位和测速精度均相对较差。需要说明的是在一般的陆基导航系统中，这两段不依赖于陆基导航。

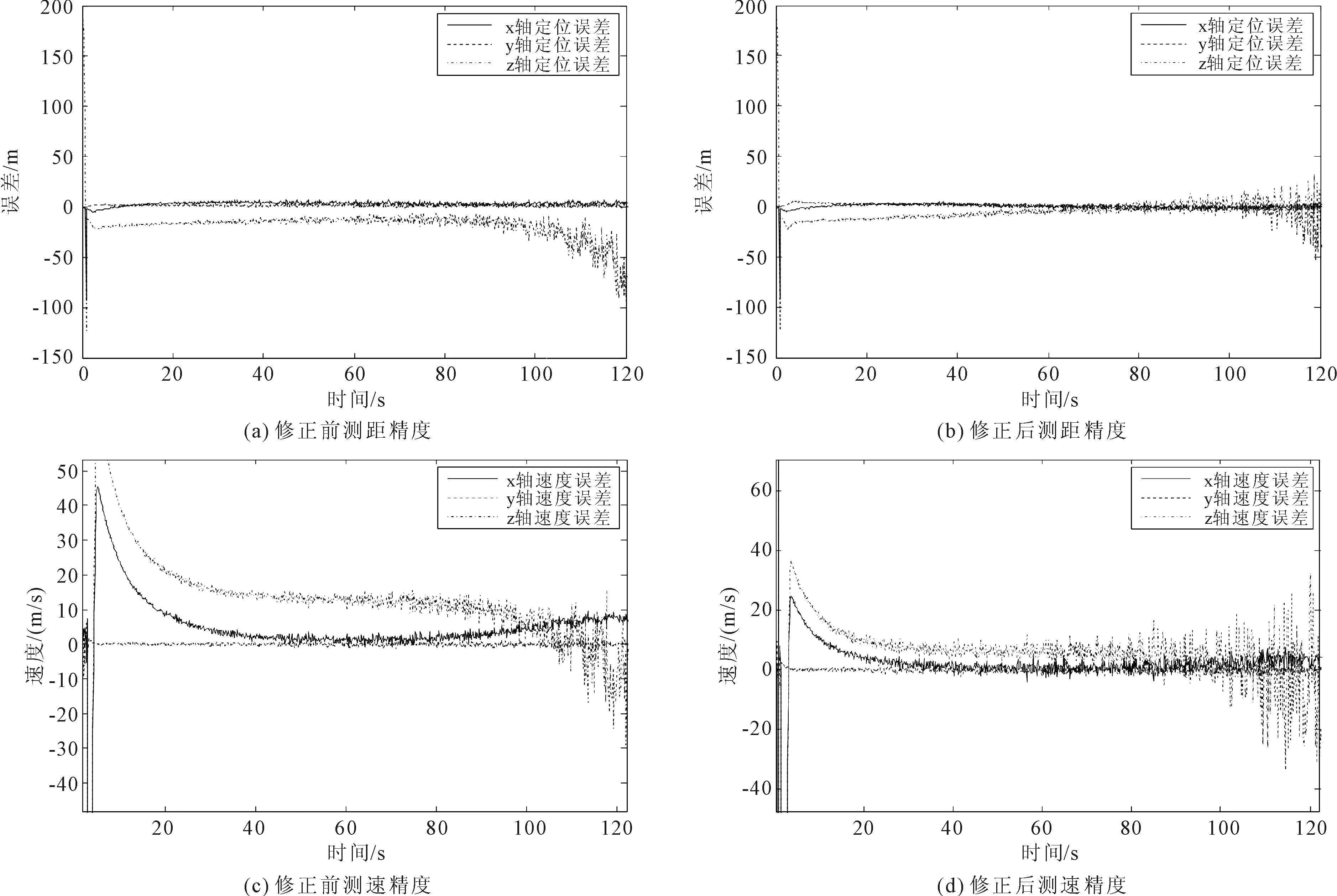
图3 修正前后对定位和测速的精度

4 结论

无线测距测速的方法，可以进行独立的无线导航。本文方法主要是在没有其他测速设备的前提下进行独立的无线测速方法，是无线测速测距的结合。在没有惯导系统等测速方法的条件下，该方法既可以将速度信息提供给测距系统进行多普勒频移的处理，也可以获得飞行物本身的速度信息。在飞行器飞行中段，该方法提供了较好的测距测速精度。这样，在一定区域内，在布站较为合理的前提下，可以得到精度良好的测速测距结果[10-12]。在不依赖于卫星导航的前提下，可以达到无线导航的目的。