基于曲率模型修正的星载DDM建模与仿真

刘原华, 李 雪, 牛新亮

(1. 西安邮电大学 通信与信息工程学院, 陕西 西安 710121； 2. 中国空间技术研究院 西安分院, 陕西 西安 710000)

全球导航卫星系统反射信号(global navigation satellite system-reflection，GNSS-R)技术[1]，通过接收、处理经过地表散射的全球导航卫星系统(global navigaton satellite system，GNSS)信号，对反射面的物理特性和参数进行反演。其应用已扩展到海面高度测量[2]、海面风场反演[3]、海冰探测[4]和土壤湿度测量[5]等诸多领域。卫星信号发射到海面产生散射现象，镜面反射点附近的散射区域中各个散射点功率的叠加，形成时延-多普勒图像(delay-Doppler map，DDM)。DDM包含比时延波形更丰富的海面信息，可以模拟出任意场景下海面对GNSS信号的散射效果，用它可反演海面风场。

DDM建模与仿真通常基于岸基[6]和机载场景[7-8]，散射能量集中在较小的时延-多普勒范围内[9]，无需考虑地球曲率的影响，把地球当成水平面来研究。在岸基和机载场景条件下，天线覆盖范围较小，适用于中、小尺度范围的遥感探测。较大尺度范围的遥感探测在星载场景下进行，与机载场景相比，星载场景的散射能量分布在更广的时延-多普勒范围内[9]，需要考虑地球曲率的影响。

本文拟提出一种基于曲率模型修正的星载场景DDM建模方法。该方法在星载场景中，利用二分法对平面模型进行修正，使用Z-V(Zavortny-Voronovich)电磁散射模型对DDM建模，并统计分析不同风速条件下的相关反射功率波形。

1 DDM生成原理

地球大气层会干扰导航卫星信号传播，导致海面反射信号能量降低并出现衰减现象，需要从时延和多普勒两个方面探测反射信号的相关功率波形，进行相应的处理。

1.1 机载场景下的散射信号平面模型

机载场景中GNSS-R的几何关系如图1所示。机载场景下的散射信号平面模型以镜面反射点为中心划分散射区域。将散射区域划分为众多小的正方形区域，在每个小正方形区域内，分析其相对于镜面反射点的延时和多普勒频率。

图1 机载场景中GNSS-R的几何关系

卫星信号经过海面交界处反射和散射后进入接收机，不同的散射点所对应的延迟时间不同。

令路径r处信号传播时间与镜面反射点处的时间延迟[10]为

Δτ=τ(r)-τ0。

(1)

其中，τ0为发射机到镜面反射点处信号反射路径的传播时间，τ(r)表示路径r的传播时间。与时间延迟Δτ相等点组成的反射面上的曲线即为等延迟环。

由于接收机、GPS卫星和散射点三者之间存在相对运动，导致不同散射点散射信号的多普勒频率不同，其中具有相同多普勒频率的海面散射点组成的曲线即为多普勒线[12]。

多普勒线第r个路径散射点与镜面反射点处的多普勒频率关系[10]的表达式为

Δf=fD(r)-f0。

(2)

其中f0为镜面反射点处的多普勒频率，fD(r)表示第r个路径处的多普勒频率。

1.2 散射信号相关功率

利用海面反射信号的相关功率Z-V模型描述任一点处散射功率，得到GNSS信号在海面散射区域中任意点处的时延τ-多普勒频移f相关功率[11]表达式为

(3)

其中，〈·〉表示求均值；Ti为相干积分时间；ρ≤为积分散射单元，G(ρ)为天线增益分布；L为伪随机码自相关函数，L2表示等延迟区；Rt和Rr分别表示发射机、接收机到ρ处的距离；c为光速；δf(ρ)为变量f与散射单元ρ处的频移差值，S[δ(f(ρ))]为多普勒滤波函数，|S[δ(f(ρ))]|2表示多普勒区；σ0表示散射系数，与海面的反射系数和粗糙度等有关。

2 基于曲率模型的星载DDM

星载场景下需要考虑地球曲率因素的影响，利用利用二分法对平面模型进行修正，模拟星载散射信号的相关功率。

2.1 星载场景下几何关系

星载场景中几何关系如图2所示。

图2 星载场景下GNSS-R几何关系

其中，SSP表示镜面反射点位置，O为地心，S1为平面第一等延迟环处各散射点的位置，S为S1的投影点位置，R1和R2分别表示GNSS卫星和接收机到S1处的距离，Rd表示GNSS卫星到接收机的距离。

2.2 基于曲率模型修正的DDM

根据图2所示的几何关系，在S1处，发射机、接收机与散射点的几何关系为R1+R2-Rd=Δ，Δ为S1处几何关系的距离差。令a和b分别表示接收机、GNSS卫星与S处之间的距离，则S处的几何关系为a+b-Rd>Δ。

(1) 利用二分法修正平面模型

令S3表示S1和SSP的中点位置S2所对应的投影点位置，用R3、R4分别表示GNSS卫星和接收机与S3之间的距离。考虑地球曲率的影响，利用二分法[12]修正平面模型，其流程如图3所示。

图3 模型修正流程

基于曲率模型修正的步骤如下。

步骤1取S1和SSP的中间值所对应的投影点位置为S3。

步骤2若R3+R4-Rd<Δ，则将SSP的坐标转换成S2处的坐标；若R3+R4-Rd>Δ，则将S1的坐标转换成S2处的坐标。

步骤3重复上述步骤，直到S3处的几何关系满足R3+R4-Rd-Δ<1，结束循环，退出迭代。

(2) 计算投影点坐标

修正平面模型后，需要计算投影点坐标。采用WGS-84地球模型参数[12],即长轴、极扁率、偏心率分别取

(4)

其中z2表示S2处的z轴坐标。

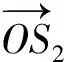
(5)

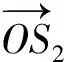
(6)

(3) 生成相关功率波形

利用二分法和投影点的计算方法可找到曲率模型下的第一等延迟环。此时可在曲率模型中的散射区域进行散射单元的划分，建立曲率模型下的几何关系。基于曲率模型，利用公式(3)中由σ0、L2、|S[δ(f(ρ))]|2、G(ρ)决定的散射区域中等延迟区、等多普勒区相关交叉区域的几何关系进行散射单元的积分，可得到相应的散射信号相关功率。

3 实验结果及分析

给定风向、卫星仰角等条件，使用Matlab作为编程工具，分别对机载场景模型和星载场景模型的相关功率进行仿真。机载场景下设定接收机高度为5 km[8]，星载场景下设定接收机高度为500 km[13]。

对平面模型和曲率模型的第一等延迟环区域范围仿真结果如图4所示。

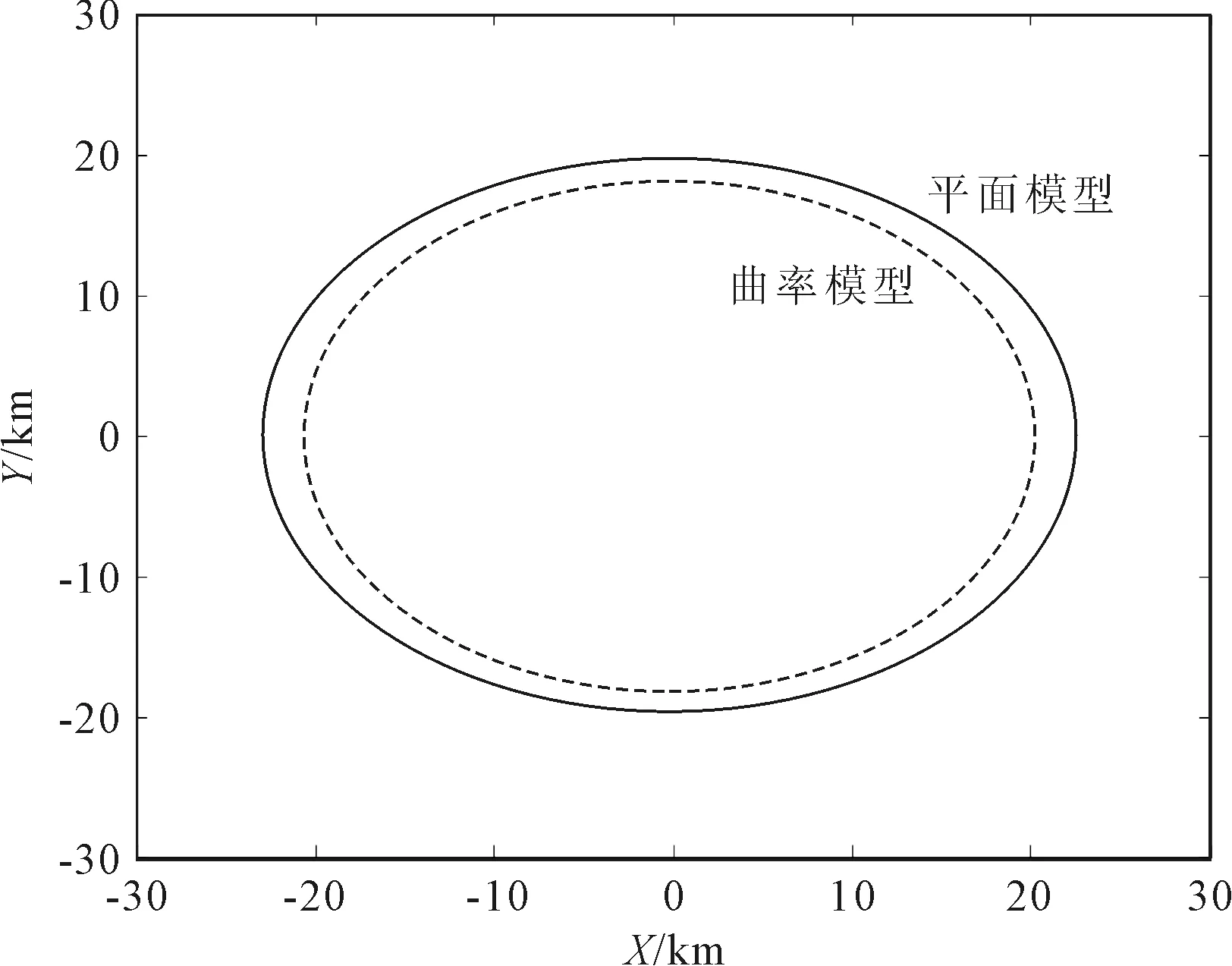
图4 平面模型和曲率模型第一等延迟环

从图4中可以看出，基于曲率模型修正的第一等延迟环的区域范围比平面模型下第一等延迟环的区域范围小，所对应的散射信号能量区域也较小。

在风向、卫星仰角等条件相同，不同风速条件下，多普勒频率为0时，基于曲率模型修正下的散射信号相关功率波形的仿真结果如图5所示。从图5可以看出，在风速分别为2 m/s、6 m/s、24 m/s、70 m/s时，随着风速的增大，散射信号的相关功率峰值逐渐变小。

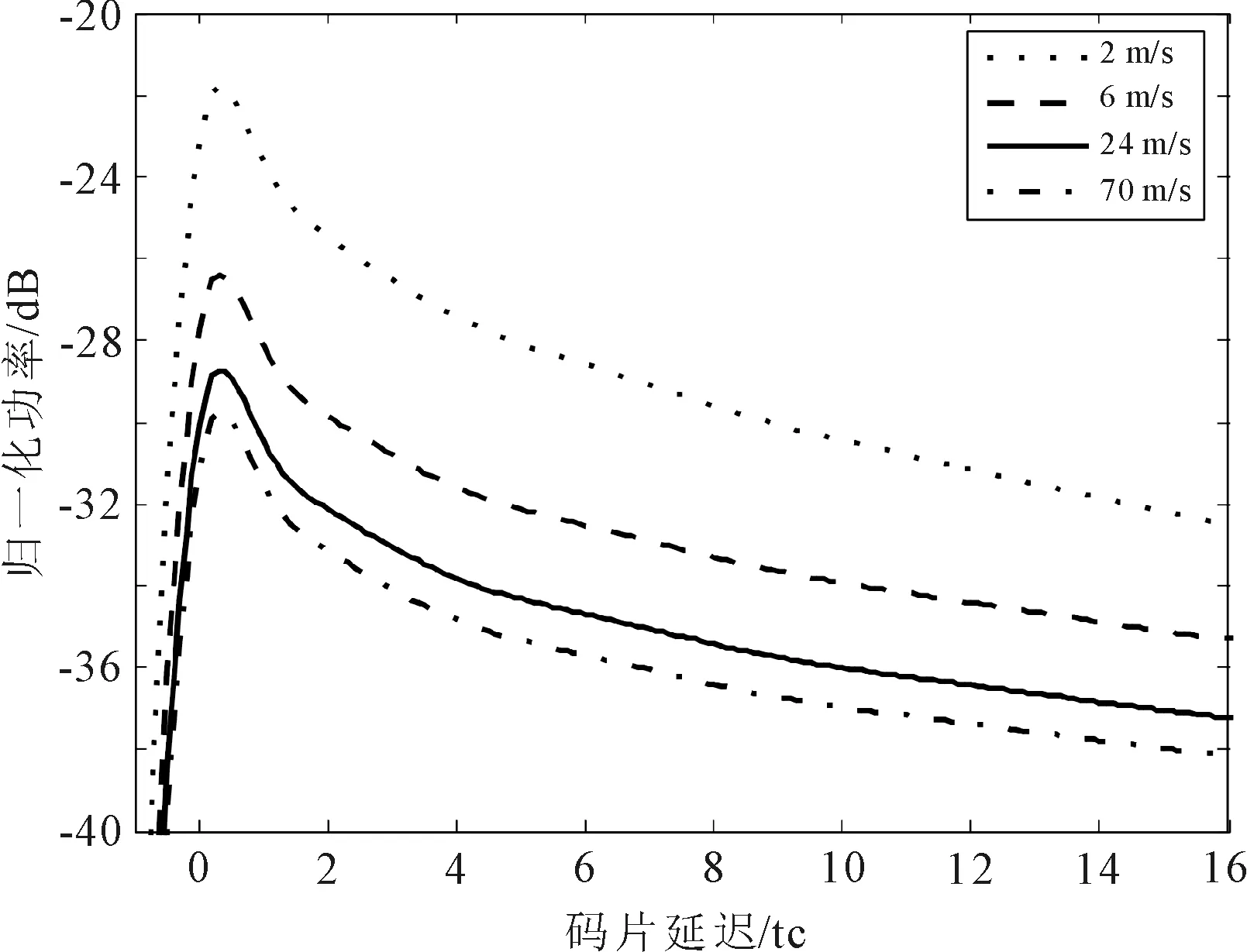
图5 不同风速条件下的功率波形

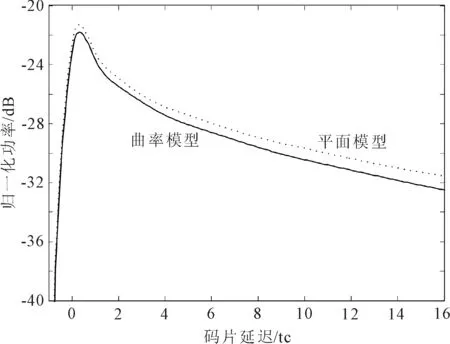
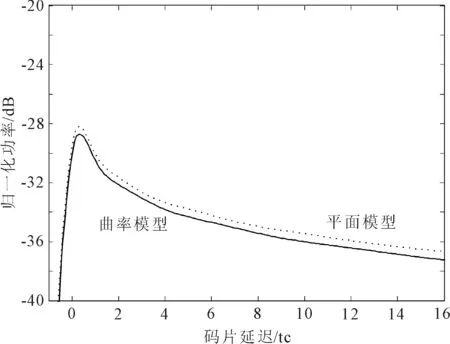
风速为2 m/s、6 m/s、24 m/s、70 m/s时，不同模型下的相关功率波形对比情况如图6所示。

由图6可以看出，不同风速条件下的平面模型的相关功率波形峰值略高于曲率模型下的功率峰值，散射信号相关功率波形无太大差异。平面模型中，2 m/s低风速时散射信号相关功率峰值为-21.29 dB，且随着风速增加至70 m/s相关功率峰值降至-29.26 dB。星载曲率模型中，2 m/s低风速时散射信号相关功率峰值为-21.81 dB，且随着风速增加至70 m/s相关功率峰值降至-29.76 dB。这是因为基于曲率模型修正的第一等延迟环范围减小，使得对应的散射信号能量区域减小，散射信号的相关功率波形峰值较低。

4 结语

基于星载曲率模型，提出了一种利用二分法进行模型修正的方法。在曲率模型下的几何关系与平面模型下的几何关系误差小于1的条件下，找到曲率模型下的第一等延迟环，完成模型修正，并基于Z-V散射模型统计不同模型的相关功率波形。相关仿真结果表明，该方法缩小发第一等延迟环范围，减小了散射信号，导致曲率模型下的相关功率峰值略低于平面下的相关功率峰值，但整体上，波形无太大变化。