一道2019年中考考纲几何题的多种解法

励钟丹

(浙江省慈溪市宗汉锦纶中学，浙江 慈溪 315301)

人们常说：数学是思维的体操，数学中一题多解的训练不仅可以让学生体验成功的喜悦，而且能提高学生综合运用数学知识的能力，开拓思维的灵活性。

下面我们来看这么一道题目：

原题：2018年山东省滨州市中考题

如图，在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE=,∠EAF=45°,则AF的长为.

现以2019年宁波中考考纲评估卷一中的一道压轴题为例,从不同的角度给出多种解法,一同体验数学解题的乐趣.

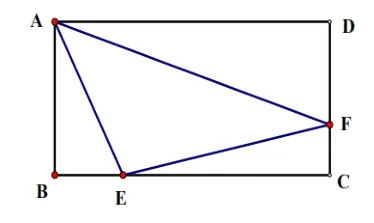
题目如下：如图,矩形ABCD的边长AB=2,AD=4,点E,F分别在线段BC和线段DC延长线上.若,∠EAF=45°,则AF的长为()

解法1：构造等腰直角三角形,即“K”字型,得到全等三角形,利用全等三角形对应边相等的性质以及相似三角形的性质求解。

如图,连接EG,过G作GM⊥AD于M,作GN⊥BC于N,

由∠EAF=45°,易证△AGE为等腰直角三角形,则AG=EG,

由“K”字型,易证△AMG≌△GNE,设MG=NE=x,

解法2：构造等腰直角三角,即“K”字型,方法和解法1类似.

如图,过E作EG⊥AE交AF于G,过G作GQ⊥AD于Q,作GH⊥BC于H,由∠EAF=45°,易证△AGE为等腰直角三角形,则AE=GE,由“K”字型,易证△ABE≌△EHG,则EH=AB=2,

解法3：构造等腰直角三角形,即“K”字型,和上述两种方法类似.

如图,过F作FG⊥AF交AE的延长线于G,过G作GM⊥AB于M,作GH⊥DC于H,由∠EAF=45,易证△AGF为等腰直角三角形,则AF=GF,由“K”字型,易证△ADF≌△FHG,设DF=HG=x,HF=DA=4,

则MG=4-x,AM=DH=2+x,再由△ABE∽△AMG,可得,故,求得,故AF==.

总结：以上三种解法都是利用45°角构造等腰直角三角形,通过“K”字型,结合全等和相似的性质解得。

解法4：构造一线三等角,利用相似三角形的性质求解。

如图,延长AB至G,连接GE,使∠G=45°,延长BA至H,连接FH,

又∠EAF=45°,由“一线三等角”,可证△AGE∽△FHA,

通过这道题目的多种解法,可以提高学生的发散性思维,提高学生综合运用数学知识的能力,也可以让学生感受数学的不穷魅力,体验成功的喜悦。