高铁车站到发线计划非常态调整模型与算法

赵天蔚

摘  要：针对非常态下高铁车站组织作业秩序受到的影响，对高铁车站到发线计划实时调整进行研究。提出基于乘降因子的到发线计划调整方法，并对其可行性进行分析。以到发线计划乘降因子的波动性和均衡性最优为目标，构建高铁车站到发线计划实时调整模型问题，设计基于三种优先权规则的实时调整算法。最后通过算例验证该模型和算法的有效性，可为高铁车站到发线计划的实时调整提供有效依据。

關键词：到发线计划;非常态调整;乘降因子;稳定性;均衡性

中图分类号：F530    文献标识码：A

Abstract： This paper studies the real-time adjustment of arrival-departure track utilization in high-speed railway stations， aiming at influencing abnormal operation orders of high-speed railway station. On the paper， we put a forward adjustment method of arrival-departure track utilization based on carriage factor and analyzed its feasibility. In order to optimize the fluctuation and equilibrium of arrival-departure track utilization in carriage factors， a real-time adjustment model of arrival-departure track utilization in high-speed railway stations is constructed， and designed a real-time adjustment algorithm based on three priority rules. Finally， give an example to verify the effectiveness of the model and algorithm， which can provide an effective basis for real-time adjustment of arrival-departure track utilization in high-speed railway stations.

Key words： arrival-departure track utilization; abnormal adjustment; carriage factor; stability; equilibrium

0  引  言

高速铁路因具有快速、安全、便捷、舒适等优点，越来越受出行者的青睐，其客运量占比铁路客运量逐年上升，同时，在当前物流需求高速增长的情况下，高铁货运也已成为当前发展方向。倘若高速铁路受到高峰期客流、列车晚点、突发天气、安全事故和自然灾害等非常态干扰因素的影响，破坏高速铁路车站到发线计划稳定性，势必影响高速铁路运能，降低其在交通运输系统中的竞争力[1]。因此如何通过人工干预和实时控制快速实现高铁车站到发线运用计划的调整，编制适应当前阶段运营环境的新到发线运用计划已成为高铁车站智能管理的关键。

Kroon L G[2]和T?rnquist J[3]等（1997，2007）分析车站的技术作业过程，以列车晚点传播理论和最短路问题为基础，对列车运行图的稳定性问题进行了探究;张英贵等[4]（2011）在引入时间窗、权重、有限度的基础上，建立股道运用排序模型，基于三种改进解的策略得到股道运用改进方案;Sels P[5]（2016）构建分配多车站列车为目标的模型，完成车站股道编排方案优化问题;Dewilde等[6-7]（2013，2014）将问题分为进路、时刻表、到发线三个模块，求解具有健壮性的运行图及编排股道运用方案;Burggraeve S等[8]（2015）继续拓展Dewilde的方法，将旅客规模引入到进路模块，作为衡量指标，使得编制方案更具有人性化;吕红霞等[9]（2016）对铁路出行旅客进行类别划分;张英贵、刘青意等[10]（2018）统筹考虑列车类型、牵引性质、运行速度、作业类型等因素，构建旅客列车到发特征聚类指标体系，给出一种基于模糊C均值聚类的列车密集到发峰期确定方法。

已有研究中主要从车站技术作业角度出发，对晚点列车调整的优先级进行排序。本文为了更好地利用高铁车站组织设备，将引入乘降因子作为调整参考指标，对非常态高铁车站到发线运用计划进行实时调整。

1  乘降因子分析

乘降因子为高铁列车承运的旅客和货物。铁路客运站到发线计划优化一般从到发线选用费用、到发线均衡性、旅客走行距离三方面考虑。其中前两项指标均从列车对车站到发线的影响角度出发[11]，以时间作为评判指标，旅客走行距离考虑进出站口到列车所在到发线的空间距离。但高铁车站作为旅客、货物与列车的交互场所，乘降因子规模不同，对应列车所在到发线接发的客运量与货运量也不相同，到发线的繁忙程度不同，乘降因子在车站乘降过程中对相关设备的损耗程度以及车站组织作业的难易程度也都不同（如图1，（1）（2）分别为两种到发线计划，根据列车A、C的乘降因子不同，两条到发线的使用情况也不相同），因此在到发线计划编排的过程中，不仅要考虑列车对到发线的影响，还需要考虑当前到发线计划确定站内乘降因子的影响，防止出现车站设备资源浪费和超负载情况共存。

同时，当高铁列车因非常态发生延误时，若预留缓冲时间不足以吸收列车延误时间，列车在到发线实时调整过程中与后续列车到发线计划发生冲突，势必会使乘降因子随列车到发线的变动换乘其他站台。当两列列车到发线计划发生冲突时，必须改变其中一列列车到发线计划（如图2，（1）为车站原始到发线计划，G2605/6408次列车晚点20分钟，与G3559次列车占用2号到发线冲突。共有（2）、（3）兩种到发线实时调整方法），为维持车站运营稳定性，将乘降因子作调整依据，减少乘降站台的变动，可防止乘降因子大规模移动引起车站秩序紊乱，降低运营风险，确保车站运营安全。

2  模型与算法

记高铁车站的列车集为L=1，2，…，i，…，n，按列车等级设权重为ω，站内到发线集合为U=1，2，…，u，…，m，进路集合为R=1，2，…，r，…，k，站台集合为Q=1，2，…，q，…，l;t，t分别表示列车i到发时刻;x表示列车i是否占用到发线u，x=1时占用，x=0不占用;o表示列车i是否占用进路r，o=1时占用，o=0不占用;y表示列车i是否占用站台p，y=1时占用，y=0不占用;根据铁路客货运信息系统，车站内对应车次的乘降因子是可知的，记车站内对列车i候车的乘降因子规模为P（当i为旅客高铁时，取站内候车旅客规模（单位：人）;为货运高铁时，取站内候车货物重量（单位：吨），客货换算系数为α）。本文不考虑列车到发时刻及技术作业时间的调整问题，在时间确定下实时调整到发线计划。

2.1  模  型

以到发线乘降因子波动性为第一目标，即通过减少到发线调整频次，降低实时调整计划与原计划的差异性。令ε表示列车到发线是否发生调整，则：

公式（3）为强约束，表示计划调整后，任意车站都能保证列车有股道接发;公式（4）、公式（5）为到发线约束，分别表示一列列车只能有一条股道接发，一条到发线只能被一列列车占用;公式（6）、公式（7）为进路约束，分别表示一列列车只能占用一条接发车进路;一条接发列车进路最多为V中一列列车的办理接发列车作业;公式（8）、公式（9）为站台约束，分别表示一列列车只能有一个站台接发，一个站台能容纳V中的列车数不能超过该站台最大允许接车数。

2.2  算  法

3  算  例

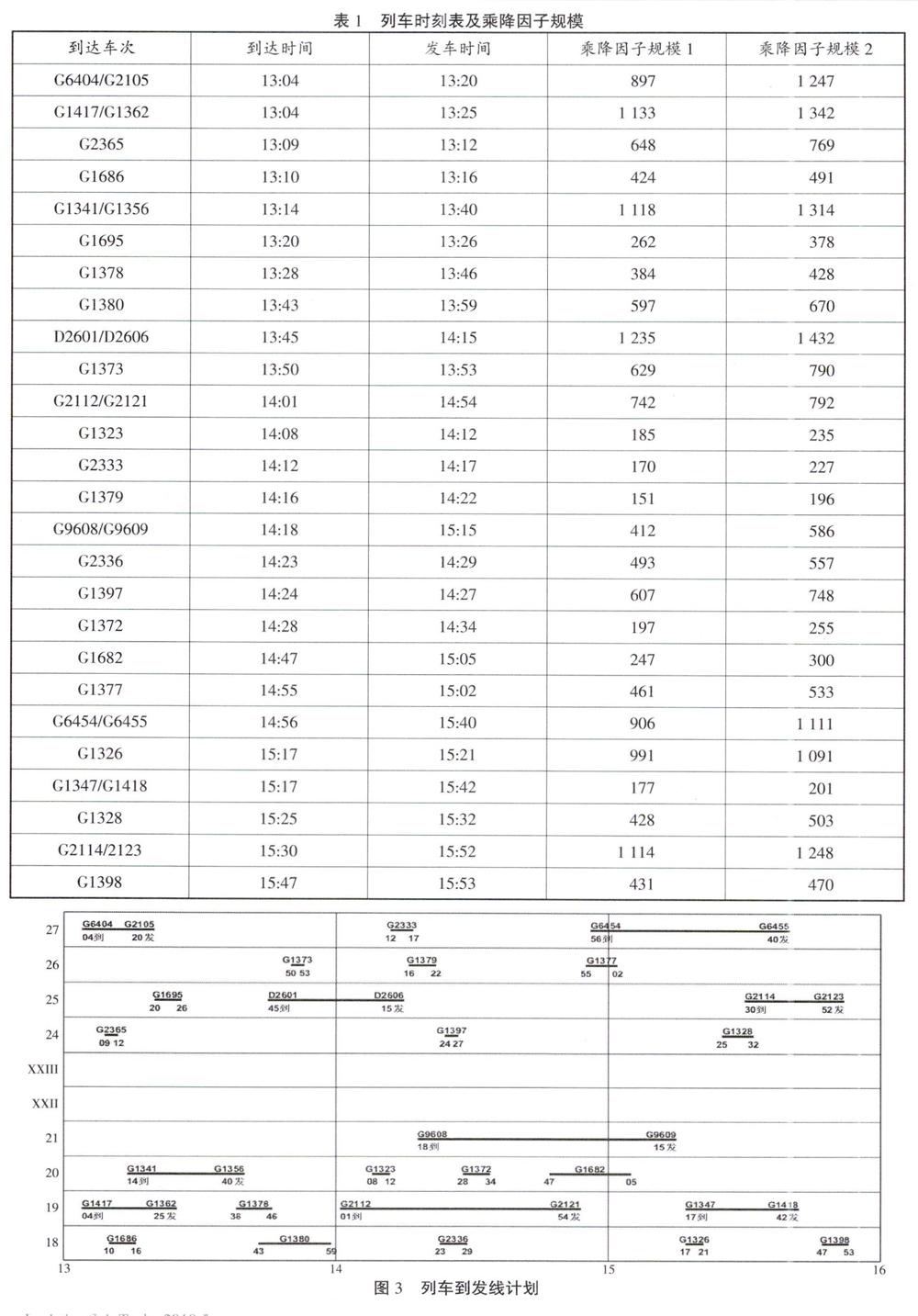
本算例选用长沙南站沪昆场13：00～16：00所有列车数据，如表1。所有列车的乘降因子均为旅客，乘降因子规模为11月采集样本，其中“乘降因子规模1”为所有样本平均数据，“乘降因子规模2”为乘降因子高峰期数据。

该时段内，长沙南站沪昆场共计有18～21、24～27号到发线在用，列车到发线运用计划图3所示。

此时，乘降因子1（非高峰期）对应站内到发线平均发送乘降因子1 880（人），到发线计划乘降因子均衡性为6.37×105，到发线计划乘降因子发送最大差值为2 837（人）;乘降因子2（高峰期）对应站内到发线平均发送乘降因子2 339（人），发线计划乘降因子均衡性为7.66×105，到发线计划乘降因子发送最大差值为3 068（人）。可知，对应高峰期下乘客占用到发线情况严重不均衡，不同到发线接繁忙程度不同，造成客流组织不均，车站设备资源存在浪费和超负载情况共存。根据本问题提到的方法，对高峰期状态下的到发线计划进行调整，算法规则优先级为列车等级原则?乘降因子均衡性原则?乘降因子波动性原则，结果如图4。

G1659次列车由原25号到发线调整至26号到发线，G1417/1362次列车由原19号到发线调整至21号到发线。此时f=1 720。发线计划整体乘降因子均衡性f=8.92×104，到发线计划乘降因子发送最大差值为783（人）。

通过结果可以看出，该方法可以有效地提高车站到发线乘降因子均衡性，使各到发线乘降因子规模趋于均衡，提高部分闲置资源利用率，降低个别资源超负载使用。

4  结  论

本文针对非常态下高铁车站到发线计划调整问题，提出了基于乘降因子的调整方法，对乘降因子在到发线计划的优化和调整过程中对车站的影响进行阐述，并对其可行性进行分析。

以到发线计划乘降因子的波动性和均衡性为目标，以到发线、进路、站台为约束，构建了高铁车站到发线计划的调整模型并设计了基于三种优先权规则的实时调整算法，

本文为将时间调整考虑在内，对非常态下列车运行图及车站到发线计划的综合考虑还需要进一步研究。

参考文献：

[1] 贾利民，王莉，秦勇. 突发事件下高速铁路运输组织——理论与应用[M]. 北京：北京交通大学出版社，2017.

[2]  Kroon L G， Romeijn H E， Zwaneveld P J. Routing trains through railway stations： complexity issues[J]. European Journal of Operational Research， 1997，98（3）：485-498.

[3]  T?rnquist J， Persson J A. N-tracked railway traffic re-scheduling during disturbances[J]. Transportation Research， Part B（Methodological）， 2007，41（3）：360-362.

[4] 张英贵. 铁路客运站股道运用优化方法与应用研究[D]. 长沙：中南大学（博士学位论文），2012.

[5]  Sels P， Cattrysse D， Vansteenwegen P. Automated platforming & routing of trains in all Belgian railway stations[J]. Expert Systems with Applications， 2016，62：302-316.

[6]  Thijs Dewilde， Peter Sels， et al. Robust railway station planning： An interaction between routing， timetabling and platforming[J]. Journal of Rail Transport Planning & Management， 2013，3（3）：68-77.

[7]  Dewilde T， Sels P， Cattrysse D， et al. Improving the robustness in railway station areas[J]. European Journal of Operational Research， 2014，235（1）：276-286.

[8]  Burggraeve S， Dewilde T， Sels P， et al. Improving passenger robustness by taking passenger numbers and recurring delays explicitly into account on the tactical level[C] // Proceedings of 6th International Seminar on Railway Operations Modelling and Analysis （IAROR） -Rail Tokyo， 2015.

[9] 呂红霞，王文宪，蒲松，等. 基于聚类分析的铁路出行旅客类别划分[J]. 交通运输系统工程与信息，2016，16（1）：129-134.

[10] 张英贵，刘青意，雷定猷，等. 铁路大型客运站旅客列车到发特征聚类分析[J]. 物流科技，2018，41（3）：69-73.

[11] 刘伟. 非常态下的大型客站咽喉利用与到发线分配优化研究[D]. 北京：北京交通大学（博士学位论文），2017.