切换拓扑企业创新时滞演化博弈
苏 雪,徐 勇,樊旭娇
(河北工业大学理学院,天津 300401)
0 引言
企业合作创新是企业间的一种联合创新行为,能够为企业的技术学习、知识创造提供有效途径[1]。合作创新行为作为一种重要的技术创新模式,已受到学术界和企业界的广泛关注[2-4]。
创新是企业家的根本职能,企业创新活动的动力来源于对垄断利润及超额利润的追逐。企业合作创新追求的目标是纯收益最大化,有些企业为达目的,往往会采取投机行为,即利用合作企业的创新成果,但不把自己的成果分享给别人。这一行为将导致博弈演化过程中出现囚徒困境现象。若想跳出囚徒困境,让所有企业全部参与合作创新,就需要施加控制,如:政府实施奖励政策[5]、通过控制一个企业的行为而影响整个创新网络博弈的演化。
将企业视为节点,企业之间的博弈关系用边的连接表示,形成一个企业创新网络。那么,企业创新演化博弈问题就转化成创新网络演化博弈问题。企业的策略选择,取决于企业对合作创新带来的纯收益的预期。每个时刻,企业对比自身及邻居的收益情况,决定下一时刻应对其它企业的最优策略以及最优博弈网络结构。在实际应用中,博弈企业往往结合其他企业以往时刻的策略和收益进行策略选择,为实现收益最大化,可能选择不同的博弈对手或抛弃部分博弈对手,导致网络结构发生改变。本文假设企业在切换网络结构的情况下根据博弈企业前τ个时刻的信息更新策略。
网络图上的演化博弈称为网络演化博弈[6],图中的点表示博弈参与人,图的边表示博弈关系。近年来,网络演化博弈受到广泛关注。但由于网络演化博弈的复杂性以及可利用工具的局限性,有关企业创新网络演化博弈的文献凤毛麟角。程代展教授将普通矩阵乘积推广到任意维数两个矩阵乘积,并保留普通矩阵乘积的性质,提出了矩阵半张量积理论[7]。半张量积作为有效工具,可将博弈动态系统转化为相应的代数形式[8-9]。这种方法已成功应用到了布尔网络[10-12]、多值逻辑网络[13-15]、多层网络演化博弈[16]、电网的需求和控制[17-18]以及带有破产机制的网络演化博弈中[19-20]。
通过企业合作创新博弈,企业能够做出最大化自身利益的决策:参与合作创新或不参与合作创新、与哪个企业进行合作创新等。与传统地利用计算机实验模拟和微分方程分析企业创新博弈演化相比[21-22],通过半张量积理论将博弈过程代数化,企业可更加直观、简捷地观察自身在博弈中的处境,并根据博弈局势及时决定下一时刻的最佳博弈策略。同时政府可通过分析博弈演化趋势,设计合适的控制,从而使得所有企业实现合作创新。
基于以上分析,本文通过半张量积方法研究切换拓扑企业创新时滞演化博弈。首先,建立切换网络企业创新时滞演化博弈模型,利用半张量积将博弈中的企业收益、策略演化以及网络的切换分别代数公式化,得到切换拓扑企业局势演化过程的代数表达式,基于代数表达式分析博弈的局势演化特征;其次,设计控制输入,给出企业全部参与合作创新的充要条件,得到自由控制序列;最后,举例验证以上方法和结论在切换拓扑企业创新时滞演化博弈分析中的可行性。
1 预备知识
首先列出本文用到的相关符号、定义及基本性质。
1)Mm×n表示m×n实矩阵集合;
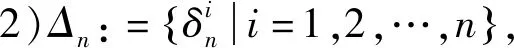
3)Coli(M)表示矩阵M的第i列,Col(M)表示矩阵M的列集合;
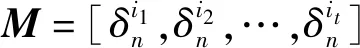
5)Vr(A)=(a1,1,a1,2,…,a1,n,…,am,1,am,2,…,am,n)T表示矩阵A的行展开。
定义1[7]设A∈Mm×n,B∈Mp×q,l=lcm{n,p}为n与p的最小公倍数,那么,A与B的半张量积定义为
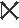
定义2[6]设M∈Mp×s,N∈Mq×s,它们的Khatri-Rao积记为M*N,定义为
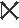
命题1[7]设X∈Rm,Y∈Rn是两个列向量,那么有
W[m,n]XY=YX
其中,W[m,n]=δmn[1,m+1,2m+1,…,(n-1)m+1,2,m+2,…,(n-1)m+2,…,m,2m,…,nm]称为mn×mn换位矩阵。
命题2[23]定义恢复因子
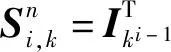
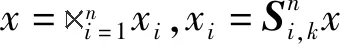
命题3[6]设X∈Δp,Y∈Δq,定义两个哑矩阵分别称为“前保持操作”和“后保持操作”:
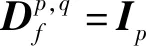
则
命题4[6]1)设列向量X∈Rt×1,A∈Rm×n,则有
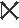
2)设X∈Δk,有
X2=Mr,kX
(1)
式(1)中
称为降幂矩阵。
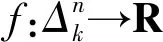
(2)
式(2)中xi∈Δk,i=1,2,…,n。
引理2[11]考虑一个k值逻辑网络
x(t+1)=Lx(t)
(3)
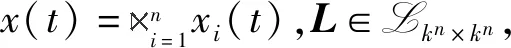
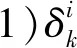
Ne=Trace(L)
2)长度为s的极限环的个数记为Cs,有
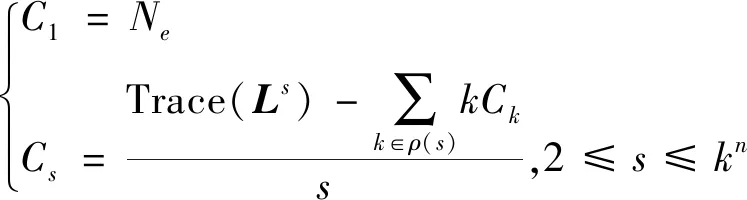
其中,ρ(s)代表s的真因子的集合,s的真因子是正整数且k 下面给出博弈论的相关定义。 定义3[6]一个正规有限博弈由以下3个要素组成: 1)n个玩家N={1,2,…,n}; 3)玩家i的支付函数pi,i=1,2,…,n。 如果博弈在确定的策略更新规则下重复进行,就称其为演化博弈。 定义4[6]一个网络演化博弈由3个要素组成,记为((N,E),G,Π): 1)(N,E)代表一个网络图; 2)G称为基本网络博弈,当(i,j)∈E是网络的一条边时,i与j重复进行基本博弈; 3)Π称为策略更新规则。 本文主要考虑切换拓扑企业创新时滞演化博弈。其中,切换拓扑是指不同时间点企业之间的博弈关系网不同,企业根据收益和策略的选择调整参与博弈的网络。时滞是指企业会根据邻居及自身前τ个时刻的策略和收益信息来选择下一时刻的博弈策略。 切换拓扑企业创新时滞演化博弈,包含以下4个部分: 1)企业创新网络集M:={1,2,…,m},每个网络的拓扑结构都是一个连通无向图 (N,εz),其中N:={1,2,…,n}为企业集,εz:={(i,j),i,j∈N}是边集,表示企业i和j在网络z上存在博弈关系,z∈M; 2)企业创新基本网络演化博弈:如果(i,j)∈εz,那么t时刻,在网络z上企业i和企业j分别以策略xi(t)和xj(t)进行基本网络演化博弈,xi(t),xj(t)∈S0={1,2}; 3)企业的策略更新:假设t时刻所有企业在网络z上进行博弈,策略更新表示为 xi(t+1)=fi,z(xi(t-τ+1),xi(t-τ+2),…,xi(t),xj(t-τ+1),xj(t-τ+2),…,xj(t)|j∈Ni,z) (4) 式(4)中xj(t)∈S0是玩家j在t,t=0,1,2,…时刻的策略,Ni,z是企业i在网络z上的邻居集合,j∈Ni,z当且仅当 (i,j)∈εz,i∈N,z∈M; 4)企业创新博弈网络的切换:设所有企业t时刻博弈的网络记为z(t),网络的切换为 z(t)=g(x(0),x(1),…,x(t)) (5) 表1 企业创新博弈的基本收益矩阵Tab.1 The basic benefit matrix of enterprise innovation game 由表1看出收益矩阵是对称的。 本文计算博弈网络上企业的总收益, 那么t时刻在网络z上企业i的收益函数为 (6) 式(6)中pij(xi(t),xj(t))是t时刻在网络z上,企业i与企业j分别以策略xi(t)和xj(t)博弈的收益,Ni,z表示网络z上企业i的邻居企业集合。 考虑到企业进行博弈时,都期望自身收益最高,所以本文采用时间并联型短视最优响应的策略更新规则:站在企业i的立场上,企业i认为其他企业下一时刻的策略选择和上一时刻一样,企业下一时刻的策略选择是对付其他企业上一时刻最好的策略。设其他企业在t时刻的策略局势为S-i(t),有 xi(t+1):=argmaxxi(t)∈S0pi(xi(t),S-i(t)) (7) 当企业有超过一个最优响应策略时,选择下标最小的策略作为下一时刻的策略。比如策略si,sj∈S0满足式(7),如果有i>j,那么企业i选择策略sj作为下一时刻的策略, 即xi(t+1)=sj。 企业的合作创新博弈是一个持续演化的动态过程,下面将切换拓扑企业创新时滞演化博弈过程代数公式化。 为了方便表示,定义如下符号表示向量 (8) 式(8)中yi(t)∈Δ2τ,y(t)∈Δ2nτ,y-i(t)∈Δ2(n-1)τ。 2.2.1 博弈收益代数公式化 由表1得收益矩阵 在网络z上企业i的收益函数就可表示为 (9) 2.2.2 最优策略演化的代数公式化 将Mpi,z分成 2(n-1)τ块 Mpi,z=[Blk1(Mpi,z),Blk2(Mpi,z),…,Blk2(n-1)τ(Mpi,z)] Colξi,l,z(Blkl(Mpi,z))≥Colξ(Blkl(Mpi,z)),∀ξ=1,2 令Li=[Li,1,Li,2,…,Li,m],有 xi(t+1)=Liz(t)y(t) (10) 2.2.3 网络切换的代数公式化 企业已选出在每种网络结构下对付其他企业最好的策略,这时企业需要根据所选策略预估同样的策略在不同博弈网络上的收益,然后决定下一时刻想要参加的博弈网络。基于企业采用的短视最优响应的策略更新规则,企业在t+1时刻的预估收益为 (11) 设行指标ζj满足 Rowζj(V)≥Rowζ(V),∀ζ=1,2,…,m 令Lz=δm[ζ1,ζ2,…,ζ2nτ],得到企业博弈网络切换的代数表达形式 z(t)=Lzy(t) (12) 2.2.4 博弈过程的代数公式化 综合以上几步,得到切换拓扑τ时滞企业创新网络演化博弈的代数表达式 (13) (14) y(t+1)=Lyz(t)y(t) (15) y(t+1)=Lyz(t)y(t)=LyLzy(t)y(t)=LyLzMr,2nτy(t)=Ly(t) (16) 式(16)中L=LyLzMr,2nτ。 企业博弈的演化特征可通过式(16)体现,L是企业策略局势演化的状态转移矩阵,蕴含了企业策略演化的信息。因此,博弈的演化过程与式(16)所示的代数形式等价。基于此,本文通过研究L的性质来分析博弈的演化特征,例如:博弈局势演化的均衡,包括不动点和极限环。如果博弈过程收敛到一个不动点,表示所有企业都采取同样的策略并保持不变,极限环表示企业的策略选择是呈周期性改变的。 在这一部分,研究切换拓扑企业创新时滞演化博弈的策略优化问题。目标是设计合理的自由控制序列使得所有企业全部参与合作创新。不失一般性,把第一个企业视为伪玩家作为控制输入。 通过式(10)得到网络z上带有控制的最优策略演化的代数表达 (17) yj(t+1)=xj(t-τ+2)xj(t-τ+3)…xj(t+1) (18) h(t+1)=y2(t+1)y3(t+1)…yn(t+1)=(Ly2*Ly3*…*Lyn)u(t)h(t)=Luu(t)h(t) (19) 式(19)中Lu=(Ly2*Ly3*…*Lyn)。 对式(19)变形,得h(t+1)=LuW[2(n-1)τ,2τ]h(t)u(t)=Lhh(t)u(t),其中Lh=LuW[2(n-1)τ,2τ]。则对∀t∈Z+,有 h(t+1)=Lhh(t)u(t)=LhLhh(t-1)u(t-1)u(t)=(Lh)th(1)u(1)u(2)…u(t) (20) 基于式(20),得到下面的定理。 (21) 如果式(21)成立,使得所有企业全部参与合作创新的自由控制序列可设计为 (22) 那么式(21)成立。 同时对∀t>T有 这一部分,以产品零部件生产企业创新网络演化博弈为例,来展示如何应用上述方法和结论研究其博弈过程。 考虑如下切换拓扑企业创新时滞演化博弈: 1)产品零部件生产企业创新博弈网络集M={1,2,3},每个网络图都是一个连通无向图 (N,εz),其中N={1,2,3}是3种产品零部件生产企业,εz是网络z上的边集,其中ε1={(1,2),(2,3)},ε2={(1,2),(1,3)},ε3={(1,2),(1,3),(2,3)}; 2)基本收益矩阵如表2所示: 3)企业遵循短视最优响应的策略更新规则; 4)博弈网络的切换依赖于当前时刻每种局势下最优策略在每个网络上的收益。 图1 企业创新博弈结构图Fig.1 The structure of enterprise innovation game 表2 基本收益矩阵Tab.2 Fundamental return matrix 假设3种企业规模相当,且τ=2。首先解决博弈动态的代数表达式问题。 第1步:计算每个创新网络上各企业博弈收益结构矩阵,得 Mp1,1=Mp2,2=Mp3,2= [2 2.5 2 2.5 2 2.5 2 2.5 1 0 1 0 1 0 1 0 2 2.5 2 2.5 2 2.5 2 2.5 1 0 1 0 1 0 1 0]; Mp1,2=Mp1,3=Mp2,1=Mp2,3=Mp3,3 Mp3,1= [2 2.5 1 0 2 2.5 1 0 2 2.5 1 0 2 2.5 1 0 2 2.5 1 0 2 2.5 1 0 2 2.5 1 0 2 2.5 1 0]。 第2步:在企业所有可能的策略局势下选取使得自身收益最大的策略作为下一时刻的策略。计算得 第3步:在同样的策略下,选择收益最大的博弈网络作为下一时刻参与博弈的网络。计算得Lz=δ3[3 3 3…3 3 3],即所有的企业最后将会在网络3上进行博弈。 第4步:得到切换拓扑下τ=2时滞的企业创新演化博弈的代数表达:y(t+1)=Ly(t),其中 L=δ64[22 4 22 4 13 11 13 11 22 4 22 4 13 11 13 11 49 35 49 35 41 43 41 43 49 35 49 35 41 43 41 43 为了观察博弈的演化特征,当k≥1时,计算得 L2k=δ64[43 4 43 4 13 22 13 22 43 4 43 4 13 22 13 22 49 22 49 22 22 22 22 22 49 22 49 22 22 22 22 22 L2k+1=δ64[22 4 22 4 13 43 13 43 22 4 22 4 13 43 13 43 49 43 49 43 43 43 43 43 49 43 49 43 43 43 43 43 对比两个矩阵,可以看出博弈局势的演化有3个不动点和1个极限环: 实际上,(1)中的不动点是博弈的一个纳什均衡,在此局势下任何人都不愿意改变自己的策略,因为任何人改变策略都会导致收益减少,然而,这个纳什均衡不是一个最优的状态。下面我们研究如何通过控制使得所有企业全部参与合作创新,即博弈演化收敛到最优状态。把第一个企业视为控制输入,得到带有控制的时滞演化博弈代数表达式 h(t+1)=Luu(t)h(t) (23) 其中 Lu=δ16[6 4 6 4 13 11 13 11 6 4 6 4 13 11 13 11 13 13 9 11 9 11 13 13 9 11 9 11 变形h(t+1)=Lhh(t)u(t),计算 Lh=δ16[6 1 6 1 4 3 4 3 6 1 6 1 4 3 4 3 13 9 13 9 11 11 11 11 13 9 13 9 11 11 11 11 上述分析表示,如果伪玩家选择策略2并保持不变,博弈从任意局势开始都将收敛到参与合作创新状态,并保持此局势不变。 本文首先建立了企业合作创新网络演化博弈模型,并考虑切换拓扑和时滞两个因素,使得博弈过程更加直观,切合实际。其次,利用半张量积方法,将切换拓扑下企业创新时滞演化博弈过程转化为代数演化方程,得到能够反映出每一次博弈演化特征的局势转移矩阵。然后选择伪玩家,将其视为控制输入,通过博弈控制系统的代数空间表达式给出了所有企业全部参与合作创新的充要条件,得到合适的自由控制序列。最后,仿真分析验证了方法和结论的有效性。 本文给出的方法和结果可以广泛应用于实际生活中,如:人工智能与硬件终端的合作、蚂蚁金服和银行之间的互联网金融的合作升级改造、华为和英特尔合作完善物联网连接功能等。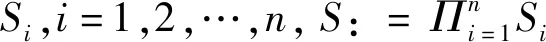
2 主要结果
2.1 模型描述
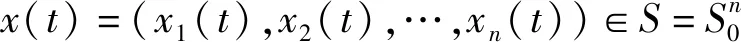


2.2 切换拓扑企业创新时滞演化博弈的代数公式化
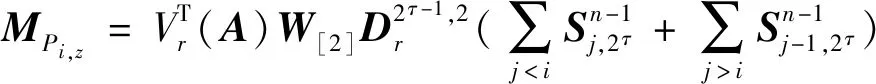
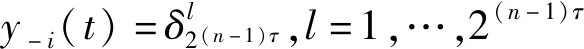
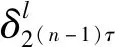
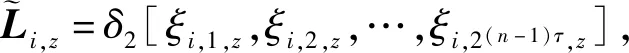
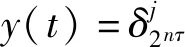
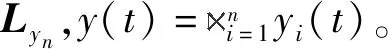
3 优化控制
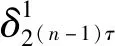
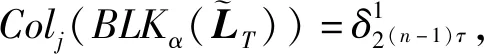
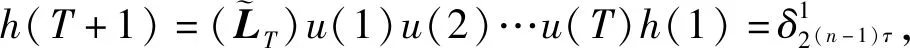
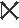
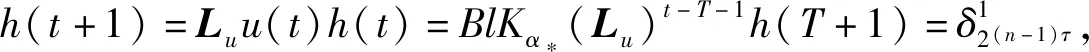
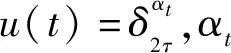
4 仿真分析


=[4 5 3 2.5 4 5 3 2.5 3 2.5 2 0 3 2.5 2 0 4 5 3 2.5 4 5 3 2.5 3 2.5 2 0 3 2.5 2 0];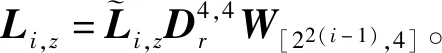
22 4 22 4 13 11 13 11 22 4 22 4 13 11 13 11 49 35 49 35 41 43 41 43 49 35 49 35 41 43 41 43]。
22 4 22 4 13 11 13 11 22 4 22 4 13 11 13 11 49 22 49 22 22 22 22 22 49 22 49 22 22 22 22 22]
43 44 34 13 11 13 11 43 44 34 13 11 13 11 49 22 49 43 43 43 43 43 49 43 49 43 43 43 43 43]
6 4 6 4 13 11 13 11 6 4 6 4 13 11 13 11 13 13 9 11 9 11 13 13 9 11 9 11]
6 1 6 1 4 3 4 3 6 1 6 1 4 3 4 3 13 9 13 9 11 11 11 11 13 9 13 9 11 11 11 11]
5 结语

