层次分析法−突变理论在煤矿煤与瓦斯突出危险性预测中的应用研究*

徐邦耘，李希建



层次分析法−突变理论在煤矿煤与瓦斯突出危险性预测中的应用研究*

徐邦耘1, 2, 3，李希建1, 2, 3

(1.贵州大学矿业学院，贵州 贵阳 550025；2.复杂地质矿山开采安全技术工程中心，贵州 贵阳 550025；3.贵州大学瓦斯灾害防治与煤层气开发研究所，贵州 贵阳 550025)

煤与瓦斯突出事故是严重影响煤矿安全生产的事故之一。为了提高对煤矿煤与瓦斯突出危险性预测的准确度，将层次分析法−突变理论引入煤矿的煤与瓦斯突出危险性预测中，通过层次分析法优化突变理论中各层指标的排序，以达到提高预测模型精确度的目的。通过对某煤矿3个煤层的实例计算，由其突变级数预测该煤层突出危险性的大小，表明基于层次分析法−突变理论预测模型在煤矿煤与瓦斯突出危险性预测中是有效的。

煤与瓦斯突出；预测模型；突变理论；层次分析法

0 引 言

目前，对于煤矿煤与瓦斯突出预测的方法很多，常用的有钻屑指标法与综合指标法[1]。传统的预测方法在时间成本与经济成本上的消耗都比较大，所以越来越多的学者开始选择用数学建模的方式来进行煤矿煤与瓦斯突出危险性的预测[2−4]。但是单一的预测模型用于实际生产中存在诸多问题，目前的预测模型大多都是基于数学方法优化后的预测模型。温廷新等[5]通过基于灰色关联熵的神经网络预测模型进行了煤层与瓦斯预测，通过灰色关联熵优化了神经网络预测模型，使得预测精确度更好；匡亮等[6]运用BP神经网络预测法对成贵高铁7座瓦斯隧道进行了煤与瓦斯突出预测；郭德勇等[7]在进行矿井瓦斯预测时，引入了突变理论的方法，通过研究，认为突变理论在煤与瓦斯突出预测中是合理且可行的。

突变理论是根据现有的模型势函数以及分歧方程推导归一公式，通过归一公式对底层指标按照重要度排序，从而得到顶层目标的突变级数的预测模型。但是，在实际预测中，底层指标的重要度受主观影响过大，所以直接应用突变理论进行预测，预测结果精确度不够高，本文通过在突变理论的基础上引入层次分析法进一步优化突变理论，使得预测结果准确度更高。

1 基于AHP的隧道煤与瓦斯突出突变理论预测模型

1.1 模型构建步骤

(1) 构建煤与瓦斯突出危险性预测指标体系。根据煤与瓦斯突出的机理，对影响煤与瓦斯突出的指标进行划分，分解为多个层级，由多个指标构成多层预测系统。

(2) 对各层指标分别进行重要度排序。根据所构建的多层预测系统，利用层次分析法进行重要度计算排序。首先需要在每个层级中对其指标进行重要度比较，按1-9的赋值构造判断矩阵，其最大特征值max要与对应的特征向量满足以下等式：

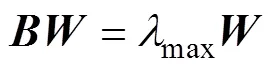
所得的max就是指标重要度值，从大到小进行排序；然后需要进行一致性检验，判断矩阵是否具有满意的一致性，否则就需对判断矩阵进行调整。

(3) 突出危险性预测。根据排序过后的多层预测系统进行突变理论预测。

表1 常见的突变数学模型势函数及其分歧方程

对表1中的突变数学模型的分歧点集方程进行变换和推导，得出尖点突变和燕尾突变两种突变模型的归一公式如下：

通过归一公式的计算求出最顶层变量值，该值就为该变量的突变级数，越靠近1危险性越大。

1.2 指标的确定与模型建立

根据相关学者[8-10]的研究，本文将煤矿煤与瓦斯突出的主要因素归结于地应力、瓦斯参数、煤的物理特性3类，在这3类中根据隧道可测量的数据分别选取以下7个指标来描述上述的3个因素，其中影响地应力的指标为：煤层埋深、瓦斯压力以及煤的孔隙率；瓦斯参数包括：瓦斯含量、瓦斯放散初速度以及瓦斯压力；煤的物理特性包括：煤的坚固性系数、煤的孔隙率和煤的焦渣特征。

由于在突变理论的运用中要求每个指标有排序，因此通过层次分析法来将每个指标进行量化，对比其重要程度，再运用突变理论来预测穿煤层隧道的煤与瓦斯突出危险性。

在地应力下的指标排序确定中，根据文献总结与专家打分的方法，确定判断矩阵见表2。

表2 地应力判断矩阵

注：其中C1代表煤的埋深，C2代表煤的孔隙率，C3代表瓦斯压力。

经计算max=3.053，对应的特征向量为[0.825 0.218 0.521]，一致性检验符合一致性。

同理在瓦斯参数的指标中，确定的判断矩阵见 表3。

表3 瓦斯参数判断矩阵

注：其中C4代表瓦斯含量，C5代表瓦斯放散初速度。

经计算max=3.018，对应的特征向量为[0.852 0.488 0.186]，一致性检验符合一致性。

同理在煤的物理特性的指标中，确定的判断矩阵见表4。

表4 煤的物理特性判断矩阵

注：C6代表煤的坚固系数，C7代表煤的焦渣特征。

经计算max=3.073，对应的特征向量为[0.394 0.902 0.172]，一致性检验符合一致性。

通过计算，准则层通过一致性检验的最大特征值对应的特征向量为[0.491 0.707 0.509]。通过计算，总排序为：

C3=0.853>C6=0.459>C1=0.419>C4=0.345>C2= 0.307>C5=0.132>C7=0.088

由此构造突变级数评价指标，如图1所示。

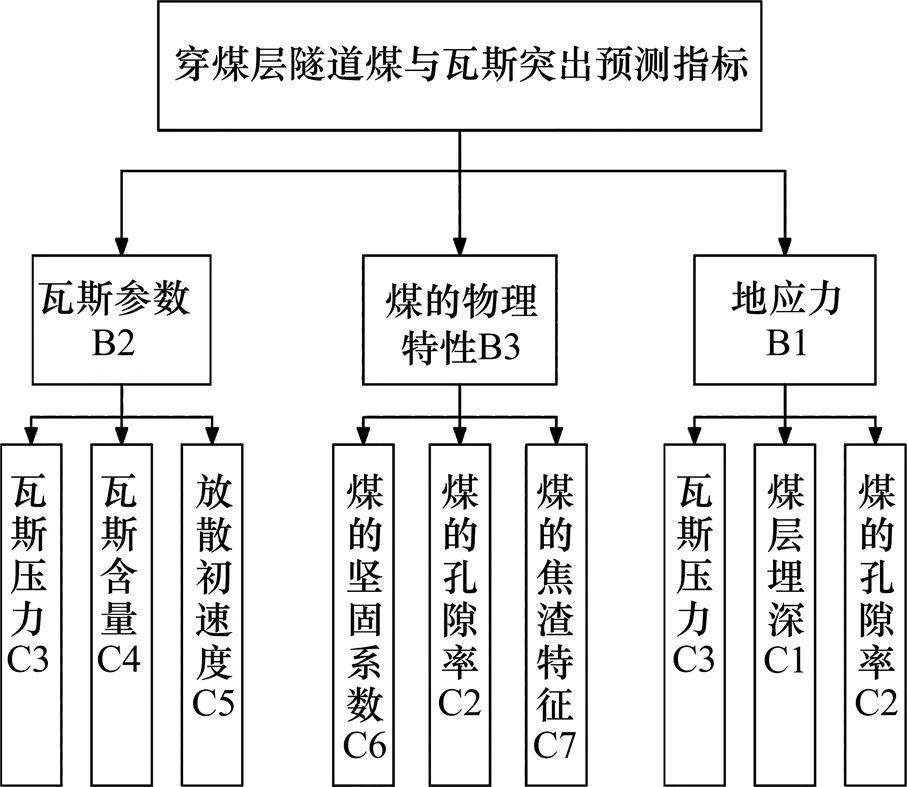
图1 瓦斯突出危险性预测评价指标体系

注：各层指标从左自右进行重要性排序。

2 实例计算

通过上文所介绍的模型，选取某煤矿的3个煤层，分别为A1煤层、A3煤层以及A5煤层，进行实例计算，根据该矿所提供的相关参数，整理出表5所示的7个煤与瓦斯突出危险性预测指标的数据，对于指标体系中数值不在0～1之间的指标，不能直接进行数值计算，需进行无量纲转换，将其取值转换为0～1之间的数量值才能进行突变级数计算，具体数据结果如表6所示。

表5 桃子垭煤与瓦斯突出危险性预测指标原始数据

表6 规范化后的煤与瓦斯危险性预测指标及突变级数数据

以A1煤层为例进行突变级数的演算。由图1可知，地应力下的C1、C2、C3指标构成燕尾突变模型，C1、C2、C3的重要程度排序为C3>C1>C2，采用燕尾突变归一公式有：

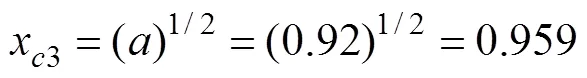
由于C1、C2、C3对煤与瓦斯突出的危险性具有互补性，共同对准则层评价指标起作用，因此，按照“互补”原则，求取平均值有：

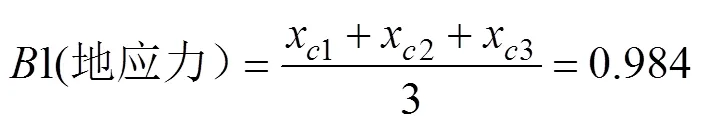
同理，在瓦斯参数准则层中，C3、C4、C5构成燕尾突变模型，其重要度排序为C3>C4>C5。由燕尾归一公式有，x3=0.959, x4=0.913，x5=0.966，按照互补原则，求其平均值，得2(瓦斯参数)=0.946。

同理，煤的物理特性准则层也满足燕尾突变模型，C2、C6、C7的重要度排序为C6>C2>C7。

通过计算得，x6=1.000，x2=0.990，x7=0.905，3(煤的物理特性)=0.965。

对于准则层目标B1、B2、B3构成燕尾突变，其重要性排序为B2>B3>B1根据燕尾突变模型归一公式有：x2=0.973，x3=0.988，x1=0.996，然后根据互补原则，取平均值，得到A1=0.986。即A1煤层的突变级数值为0.986。同理可计算其他两个煤层的突变级数值。

根据3个煤层的突变级数计算结果显示，其中A5煤层的突变级数值最大，其突出危险性最大，A3煤层的突出危险性最小，但是3个煤层的突变级数值都比较接近1，所以计算结果显示3个煤层都具有突出危险性。根据该矿的开采事实，A5煤层的突出风险为最高，这与计算结果相印证。

3 结 论

(1) 在综合分析煤与瓦斯突出影响因素的基础上，基于瓦斯突出综合作用假说机理，本文提出了突变理论预测隧道煤与瓦斯突出危险性的方法，该方法综合反映了众多复杂的影响因素，具有更高效的判别效率。

(2) 本文构建了基于层次分析法−突变理论预测模型，根据对某煤矿的实例预测计算，计算结果与实际情况相符合，验证了基于层次分析法的突变理论模型应用到煤矿煤与瓦斯突出危险性预测是可行的。

(3) 通过基于层次分析的突变理论模型对某煤矿进行煤与瓦斯突出危险性预判，并与实际情况相对比，结果显示，该煤矿的3个煤层都具有突出危险性，其中A5煤层的突出危险性最高。

[1] 国家安全生产监督管理局,国家煤矿安全监察局.煤矿安全规程.(2014 版)[M].北京:煤炭工业出版社,2014.

[2] 李 苗,张红军,陈唐军,刘夏临,王纪鹏.灰色－突变理论在尾矿坝失稳预测中的应用[J].矿业研究与开发,2014,34(5):66−68.

[3] 于海云,杨 力.基于灰色关联与SVM 模型的煤矿通风系统评价方法研究[J].煤矿安全,2013,44(1):181−184.

[4] 夏 龙,郝兵元,钱翰飞.模糊数学综合评价在矸石山边坡稳定性评价中的应用[J].矿业研究与开发,2017,37(10):33−37.

[5] 温廷新,于凤娥,邵良杉.基于灰色关联熵的煤与瓦斯突出概率神经网络预测模型[J].计算机应用研究,2018,35(11):96−100.

[6] 匡 亮,赵万强,喻 渝.BP神经网络法预测隧道瓦斯突出的模型与实例[J].铁道工程学报,2018,233(2):56−61.

[7] 郭德勇,李佳乃,王彦凯.基于黏滑失稳与突变理论的煤与瓦斯突出预警模型[J].北京科技大学学报,2013(11):1407−1412.

[8] 吴应明.华蓥山隧道有害气体监测与综合治理技术[J].现代隧道技术,2003,40(4):68−73.

[9] 袁森林,刘 旭,周建中.瓦斯隧道工程勘查技术探讨[J].四川地质学报,2009,29(1):50−51.

[10] 袁真秀,张羽军,王崇良.新寨隧道煤与瓦斯突出危险性评价及揭煤施工设计[J].四川工业学院学报,2003,22(3):88−91.

国家自然科学基金面上项目(51874107).

(2018−10−22)

徐邦耘(1995－)，男，贵州六盘水人，在读硕士生，主要从事安全科学技术相关研究，Email：790606745@ qq.com。