大采高工作面回风侧巷道群合理煤柱宽度研究

刘 建，张 松

(1. 毕节市非煤矿山安全生产监督管理站，贵州 毕节 551700； 2. 毕节市工业和信息化局，贵州 毕节 551700)

在高瓦斯矿井，由于瓦斯浓度过高，为达到通风及瓦斯抽采治理要求，一般采用以巷道群为主的多巷布置。巷道间相互扰动，由于开挖深度的加深，掘进期相互扰动效应逐渐变强[1-2]，国内多数学者采用理论分析、数值模拟等研究方式针对巷道群布置下围岩的破损机理和稳定控制技术进行了系统性的研究[3-4]. 以山西晋城寺河矿W2302工作面回风侧巷道群为研究对象，主要对其煤柱宽度进行相应的合理性验证研究。

1 工程背景

寺河矿为大采高、高瓦斯矿井，研究对象为2巷、3巷、4巷，主要研究3巷和4巷间的煤柱宽度，工作面和巷道布置图见图1. W2302工作面目前主采3#煤，并采用一次采全高开采方式，煤层埋深400～500 m，平均煤厚6.07 m，倾角4o，瓦斯含量24.7 m3/t.

根据该矿瓦斯防治安全标准，掘进时的瓦斯浓度不得高于7.9 m3/t，考虑采掘接替平衡，必须提高巷道成巷速度并将富集瓦斯抽采利用，提升抽采效率。因此，采用底板抽采瓦斯的巷道布置，2巷位于煤层地板6 m岩层处。通风方式采用“三进两回”方式，见图2，因巷道间层位不同，需从3巷与4巷间联络巷附近打通风立眼至底板2巷，以实现工作面正常通风。3#煤顶底板相关岩性力学参数见表1.

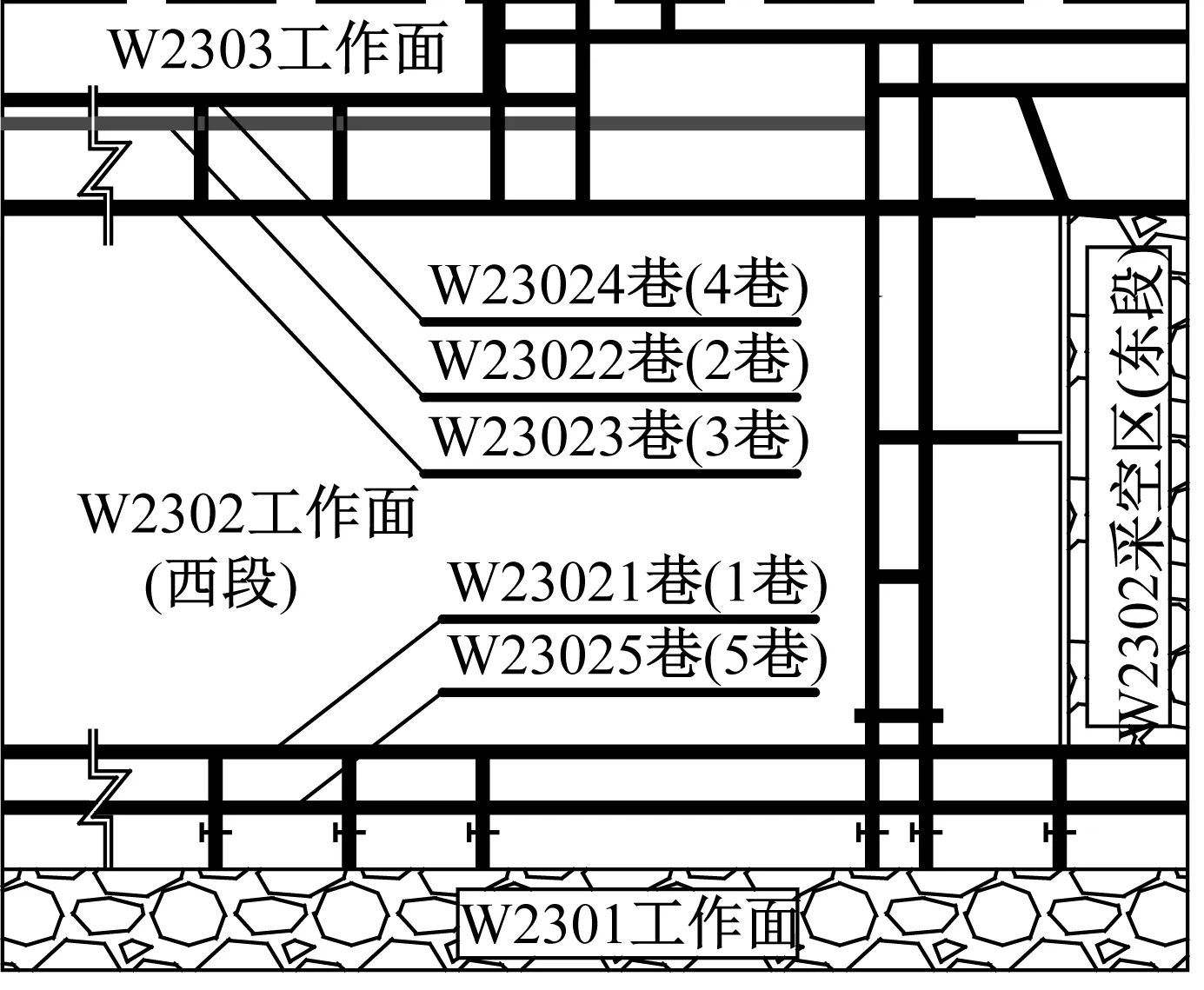
图1 工作面和巷道布置图

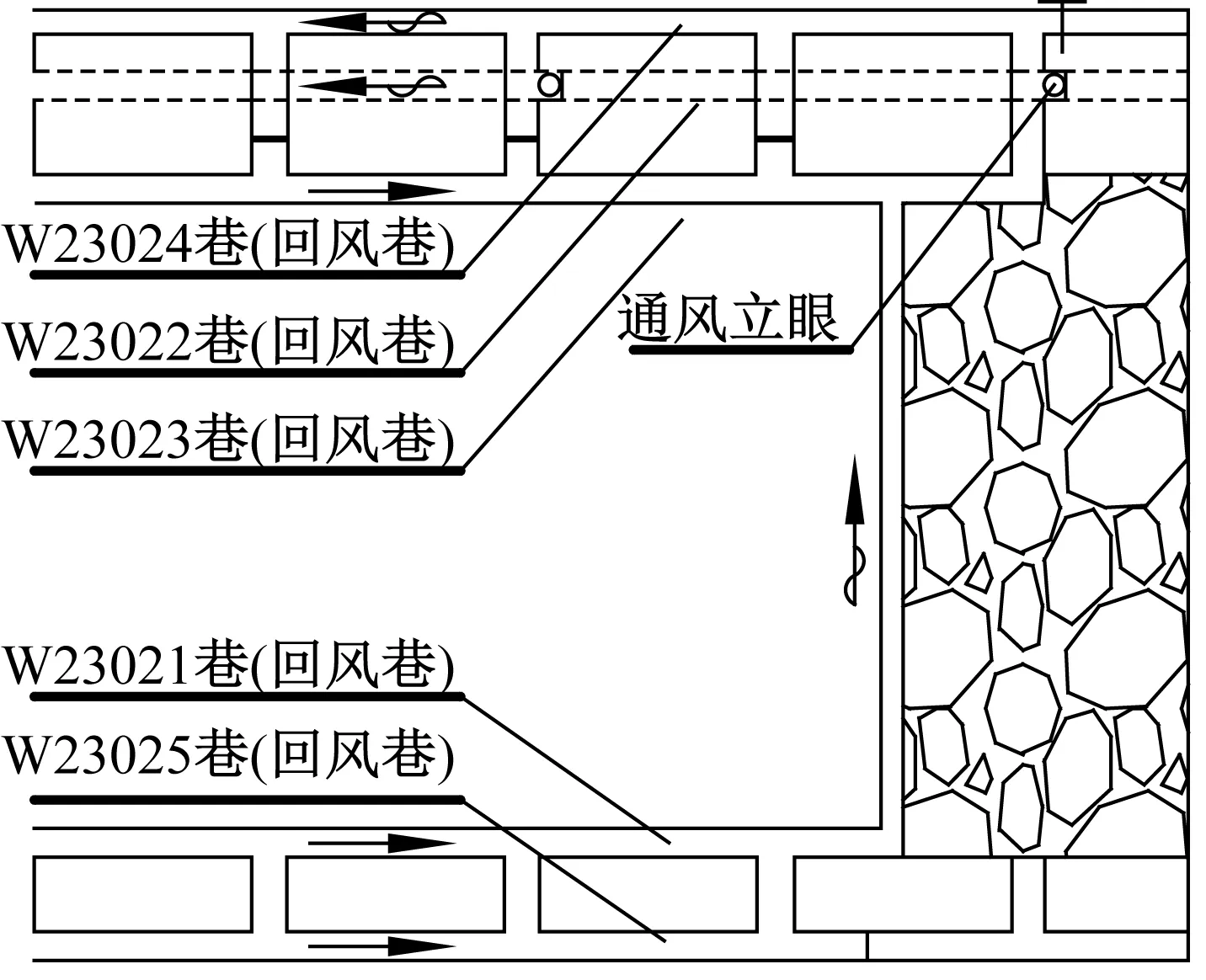
图2 通风方式示意图

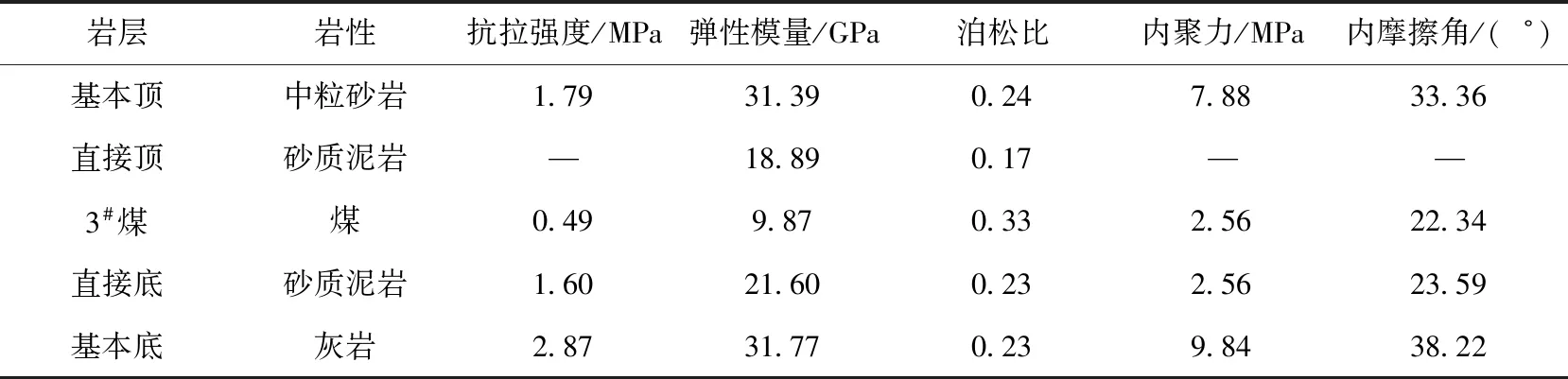
表1 煤岩体试样力学参数表

2 应力叠加分布模型确定

对3巷和4巷间合理煤柱宽度进行相应的理论研究，对现场煤柱留设宽度的合理性进行验证。

2.1 回风侧煤柱内部应力叠加分布模型

根据现场实际情况，对W2302工作面回风侧建立相应的煤柱内部应力叠加分布模型，见图3.

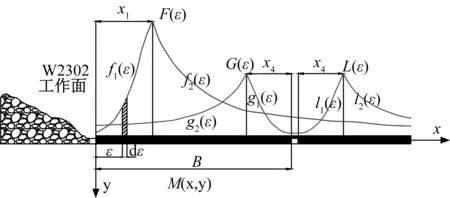
图3 现场煤柱内部应力叠加分布模型图

图3中，F(ε)曲线代表W2302工作面开挖后在煤柱形成的应力分布；f1(ε)代表塑性区内的应力分布曲线；f2(ε)即代表弹性区；同理，G(ε)、L(ε)则代表巷道开挖对左(右)煤柱形成的应力曲线；g1(ε)、l1(ε)代表塑性区曲线；g2(ε)、l2(ε)代表弹性区曲线。

煤柱内部的应力符合Weibull分布，根据文献[5]函数表达式为：

(1)

图3只是针对单个因素下的函数曲线图，但实际煤柱内应力应是工作面回采和巷道开挖后的应力叠加，留设煤柱到达一定宽度后，煤柱间原岩应力区消失，煤柱内的应力分布是由工作面回采和巷道开挖后的应力相加，并且呈一定规律重新分布，根据以上理论分析，可得工作面回采及巷道开挖后W2303工作面右侧煤体内应力叠加重新分布后函数见式(2).

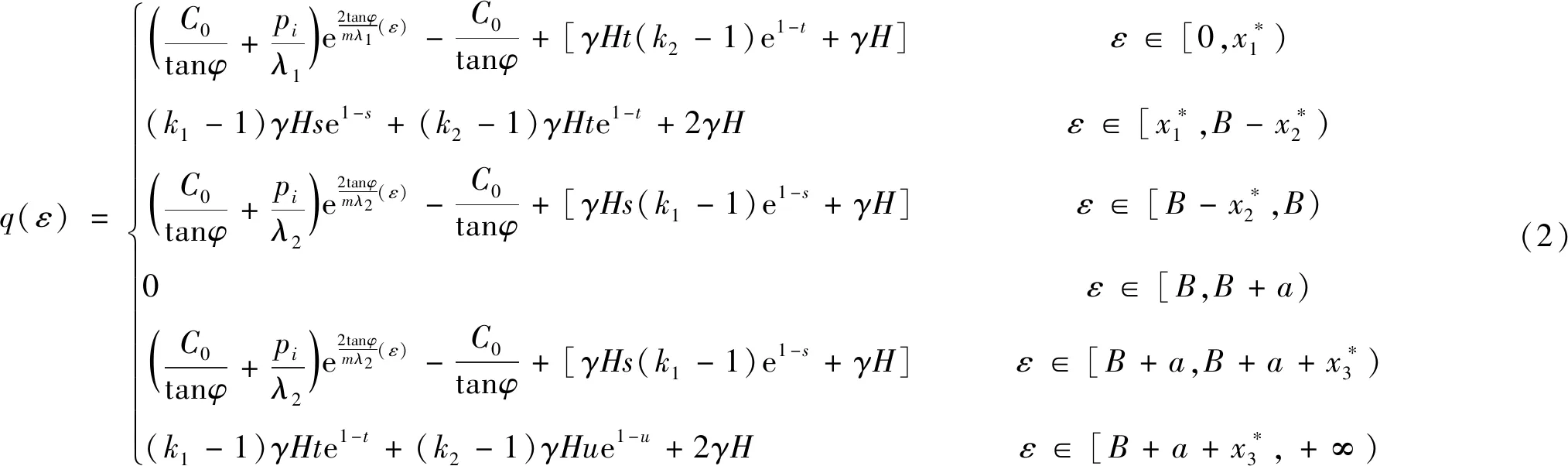
q(ε)=C0tanφ+piλ1()e2tanφmλ1(ε)-C0tanφ+[γHt(k2-1)e1-t+γH]ε∈[0,x∗1)(k1-1)γHse1-s+(k2-1)γHte1-t+2γHε∈[x∗1,B-x∗2)C0tanφ+piλ2()e2tanφmλ2(ε)-C0tanφ+[γHs(k1-1)e1-s+γH]ε∈[B-x∗2,B)0ε∈[B,B+a)C0tanφ+piλ2()e2tanφmλ2(ε)-C0tanφ+[γHs(k1-1)e1-s+γH]ε∈[B+a,B+a+x∗3)(k1-1)γHte1-t+(k2-1)γHue1-u+2γHε∈[B+a+x∗3,+∞)ìîíïïïïïïïïïïïïïï(2)

式中：

t=(-ε+xg+B-x4)/xg；

u=(xg+ε-B-a-x4)/xg；

s=(ε+xf-x1)/xf；

x1、x4—塑性区范围，m；

xf、xg—函数缓急调节参数；

λ1、λ2—侧压系数；

k1、k2—应力增高系数；

C0—内聚力，MPa；

φ——内摩擦角，(o)；

pi—锚杆支护强度，MPa，取0.2；

m—巷高，m，取3.8；

B—煤柱宽度，m；

γ—容重，kN/m3；

a—4巷宽度，m，取5.85.

式中，在ε=x1时，煤柱内最大应力为f2(ε)=k1γH.k1值即为最大应力值的主要影响因素，应力值越大，对工作面回采在煤柱内产生的支承应力的最大值影响越大，相反则越小。在ε→+∞范围中通过改变xf的值(增大或减小)，可以调节f2(ε)函数曲线的缓急程度，随着煤柱内应力逐渐向煤柱深部延伸，f2(ε)函数值将不断减小直至降低至原岩应力。同理，巷道开挖时，通过改变xg的值(增大或减小)，可以调节l2(ε)函数曲线的缓急程度。

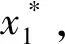
(k1-1)se1-s+(k2-1)te1-t+1=k1*

(3)

(4)

(5)

结合现场情况，利用数值模拟和理论计算对比研究得出k1、k2、xg、xf的值，其中计算参数选取如下：H=410 m(煤层埋深)，ρ=2.5×103kg/m3，煤厚6.07 m，pi=0.2 MPa，C0=0.26 MPa，φ=10o；数值计算得出单一巷道开挖后围岩垂直应力见图4，数值计算的煤柱内应力分布和xg赋不同值时煤柱内应力函数曲线见图5.

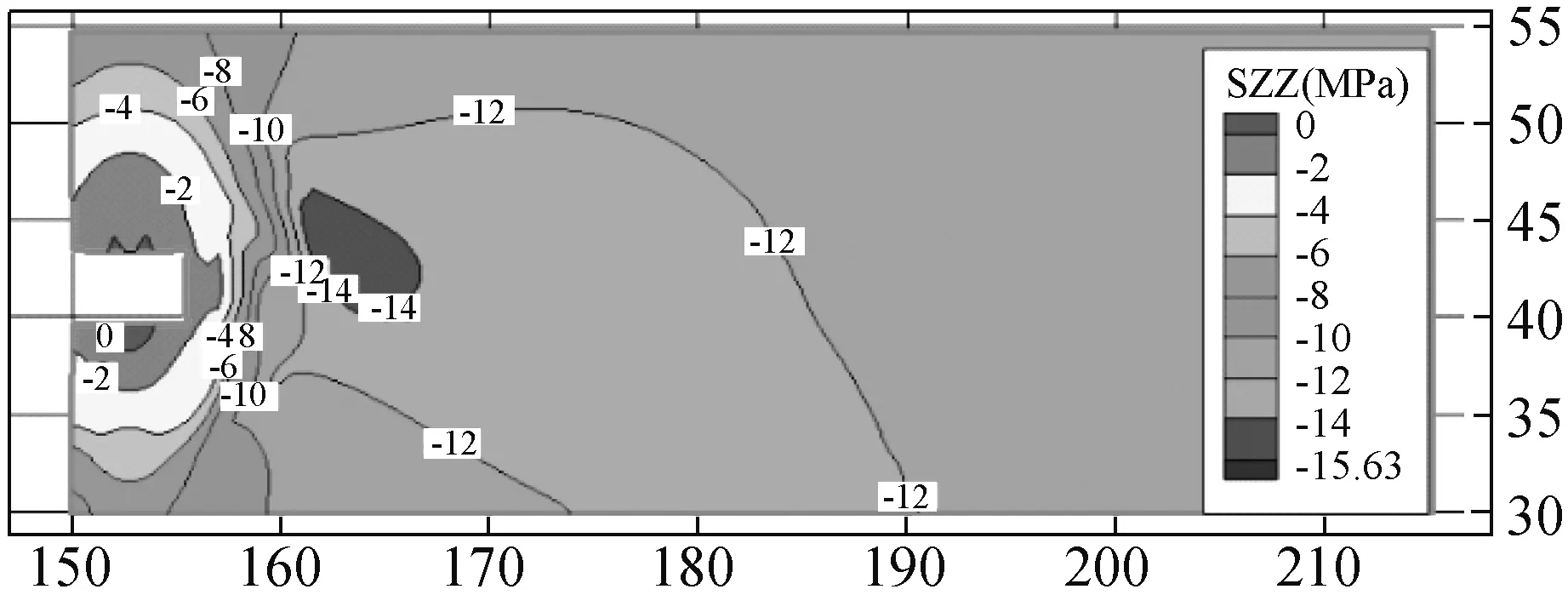
图4 煤柱内支承应力分布图(单巷开挖)

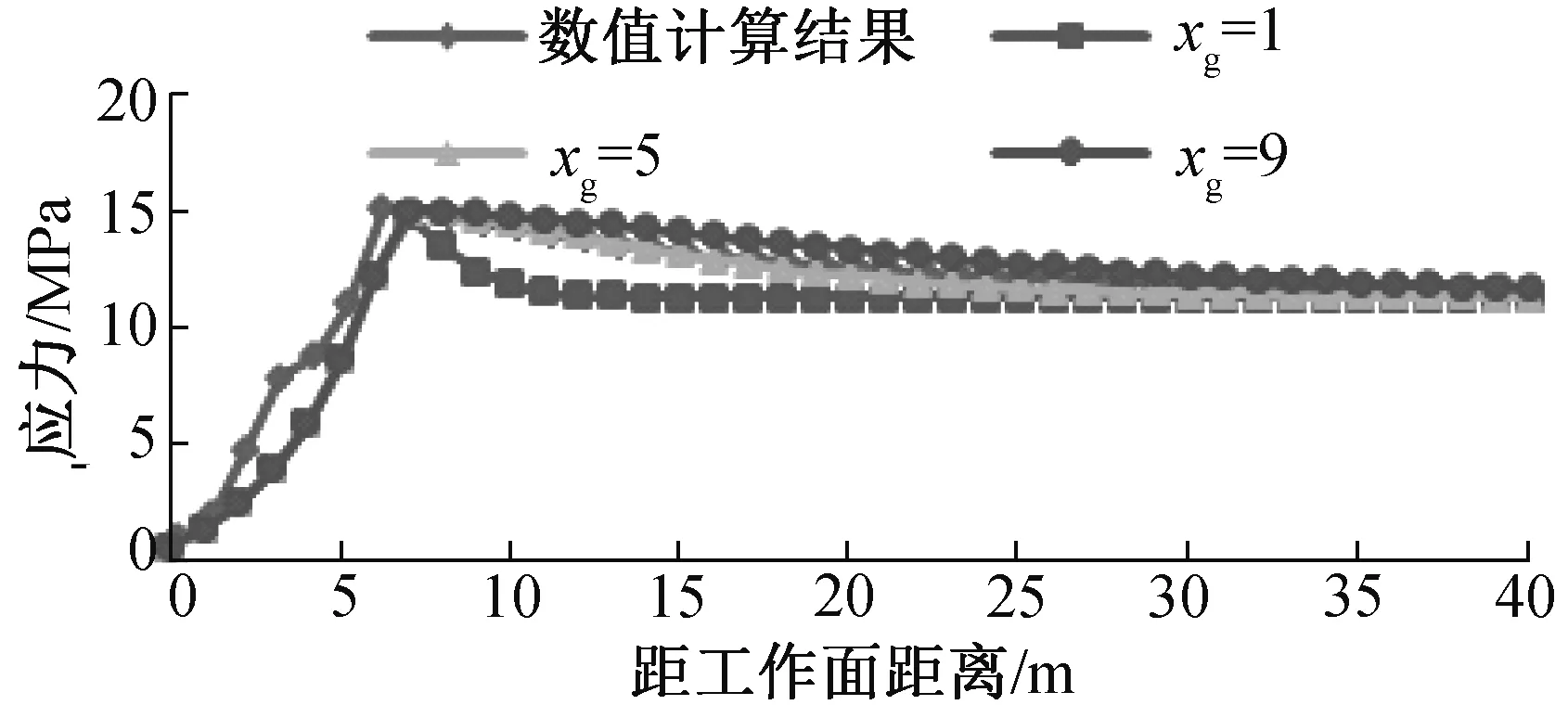
图5 不同xg时煤柱内支承应力图(单巷开挖)

由图4，5可知，k2=1.33，λ2=0.3. 在xg=5时，通过理论计算曲线和数值所得曲线基本重合，因此可以取值xg=5.

同理，模拟得出围岩垂直应力云图(单工作面回采)见图6，数值计算的煤柱内应力分布和xf赋不同值时煤柱内应力函数曲线见图7.

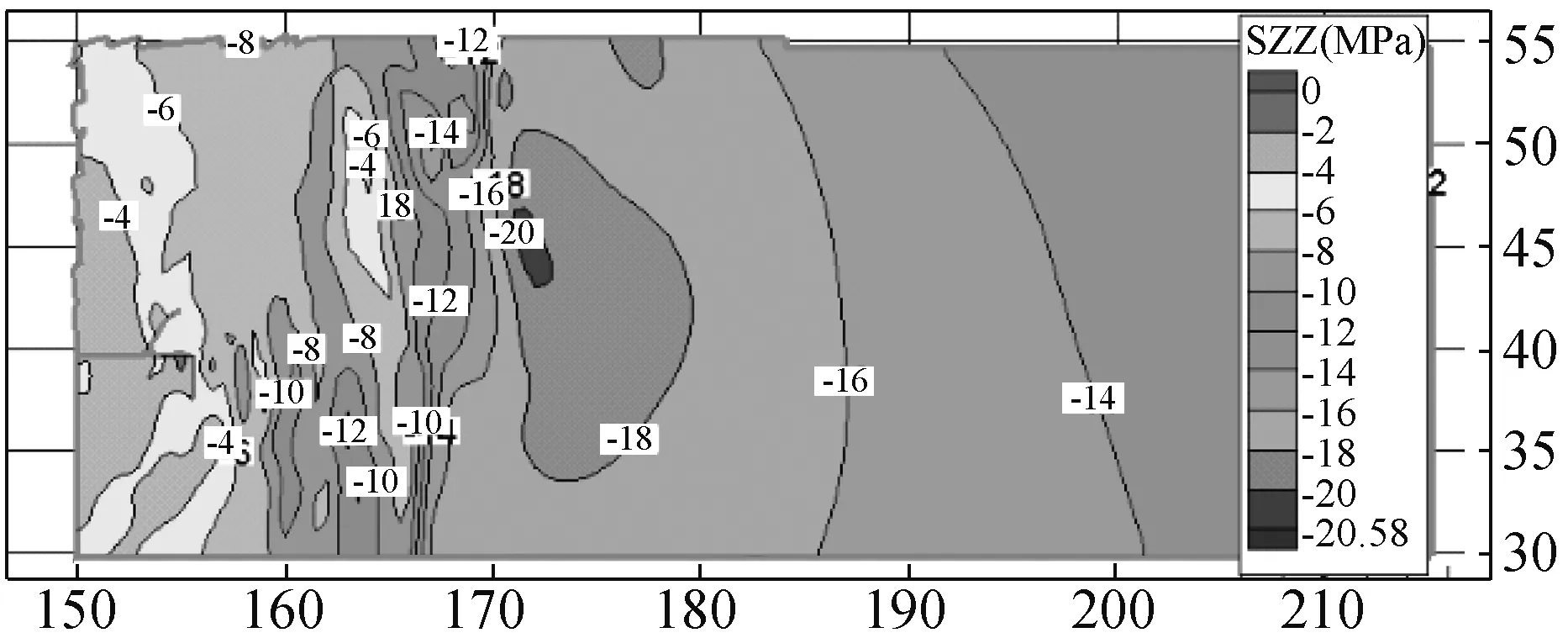
图6 煤体内垂直应力云图(单工作面回采)

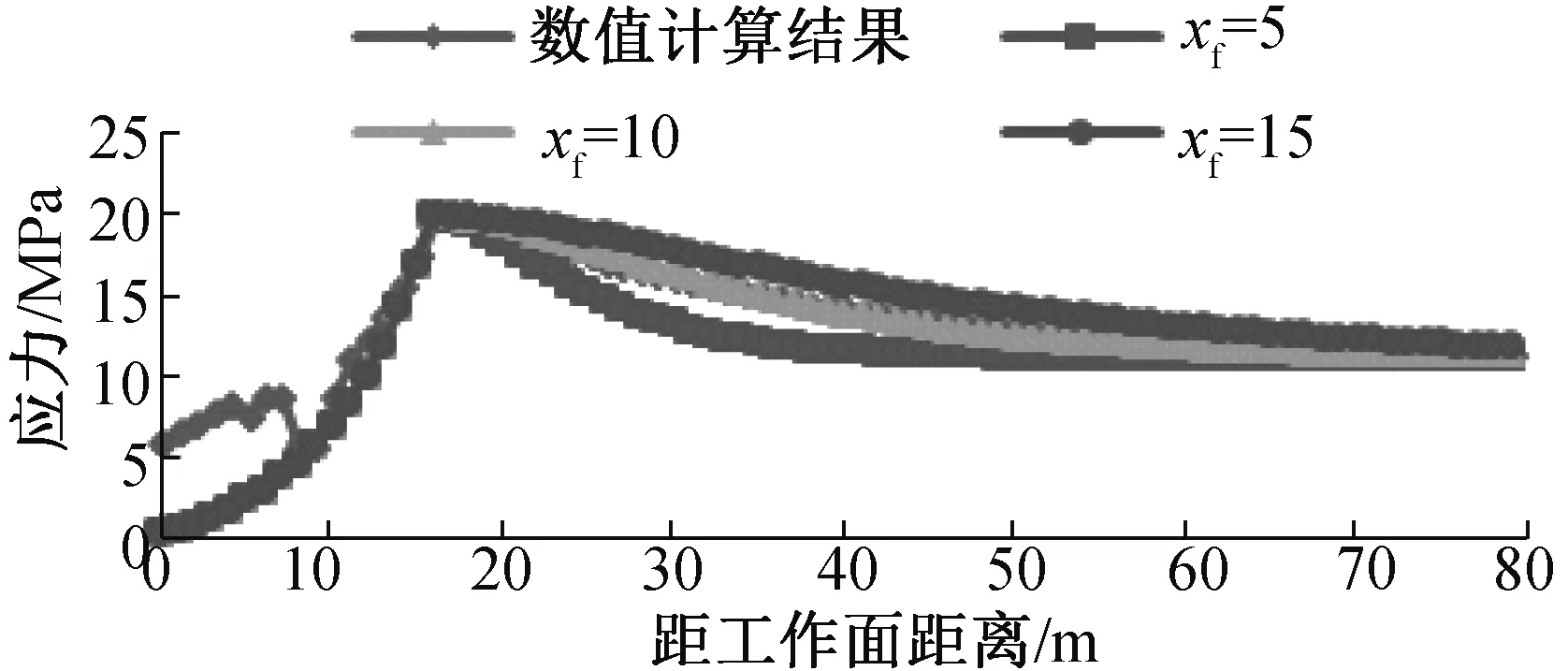
图7 不同xf时煤柱内支承应力图(单工作面回采)

由图6，7可知，k1=1.77，λ1=0.6. 其中，在距离工作面10 m范围内，理论计算的塑性区煤柱内应力低于模拟计算的结果，原因是在数值计算中煤柱受到工作面回采后的上覆岩层旋转下沉产生的水平应力，煤柱内应力受力增加较快，实际生产中，处于采空区的煤体是离散体，不能向煤柱施加水平应力。因此，在距离工作面10 m范围内，理论计算的煤柱内应力更接近现实情况，在xf=10时，距离工作面10 m以外的煤柱内应力理论计算曲线和数值所得曲线基本重合，因此，可取xf=10.

2.2 W2302工作面回风侧煤柱合理宽度确定

维持巷道稳定的煤柱宽度应满足：当煤柱左右侧皆受压变形并形成一定宽度的塑性区，煤柱中心需保留一定范围的弹性核区，并且弹性核区的宽度需大于煤柱高度的两倍，因此合理煤柱宽度应大于左右两侧塑性区宽度与两倍的煤柱高度的和，即式(6)：

(6)

式中：

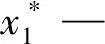
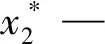
mc—煤柱高度，m，取6.

求解式(6)，得出B>37 m，由于W2302工作面回采完毕后巷道继续受到下一个工作面(W2303)的回采影响，出于安全考虑，保留安全系数1.2，得B>44.4 m，取整后W2302工作面回风侧3巷和4巷间煤柱宽度为45 m.

3 工业性试验

为验证理论研究，分析现场巷道变形规律，在2巷、3巷和4巷分别布置1个表面位移测站，为统一巷道的左右帮，规定W2302工作面推进方向左侧为巷道左帮，W2303工作面推进方向右侧为巷道右帮。测站布置见图8.

图8 回风侧巷道群测站布置图

测站1布置在2巷中，测站距切眼617 m；W23022巷左侧为W23023巷，右侧为W23024巷；测站2布置在3巷，距切眼542 m；测站3布置在4巷，距切眼412 m；现场工作面回采期间巷道表面收敛曲线见图9.

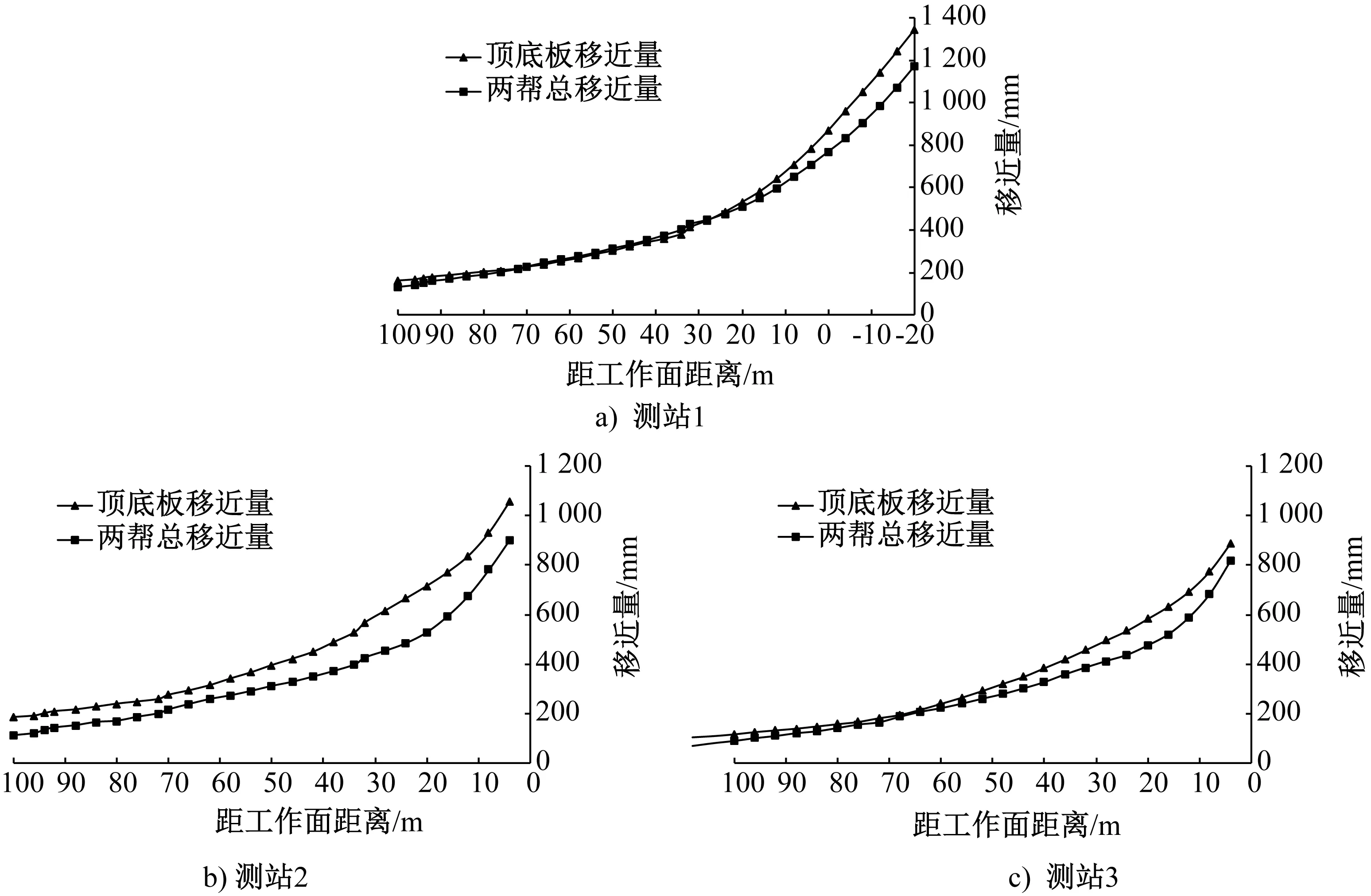
图9 巷道断面收敛曲线图

测站1和测站3是W2302工作面回采时，巷道的变形规律曲线；测站2是W2302工作面回采时，巷道表面的收敛规律曲线。由图9c)可知：在工作面超前50 m左右巷道变形曲线斜率迅速增大，此时巷道受采动影响较为严重，巷道变形速率增大；布置测站2的巷道服务于W2302工作面，由于这条巷道受到二次采动的影响，该巷道变形明显要比3巷变形严重，但是不会影响到煤炭的安全采出；测站1布置在2巷，由于其不在同一层位，巷道采用直墙半圆拱形，并且巷道掘在岩层中，虽然巷道相比其他两巷易维护，但是由于受到两次采动的影响，巷道变形要明显大于3巷和4巷。

总体看，巷道顶底板变形大于巷道两帮变形；受两次采动影响的巷道变形较大，为确保煤矿安全生产需在后期加强维护。

4 结 论

1) 建立了应力叠加分布计算模型，分析煤柱内应力分布规律并得出相应的计算式。

2) 研究得出煤柱合理宽度应大于37 m，同时考虑安全系数，煤柱宽度应大于44.4 m.

3) 经现场实测数据分析，验证W2302工作面回风侧煤柱宽度45 m是可行的，为了安全生产，后期需加强对受两次采动影响巷道的维护。