基于改进双自适应BP神经网络的故障诊断方法

李 波 , 张 琳, 张 搏, 张保山

(1. 空军工程大学研究生院， 陕西 西安 710000； 2. 93748 部队，内蒙古 包头 014000；3. 空军工程大学防空反导学院， 陕西 西安 710000)

BP神经网络是一种误差反向传播的前馈神经网络[1]，通常用误差梯度下降法更新网络。由于具备并行分布处理、非线性映射和自学习等优点，BP神经网络广泛应用于智能故障诊断[2]、健康状态预测[3]和自动控制[4]等领域。但是，因其存在易形成局部极小、学习效率低和收敛速度慢等固有缺陷[5]，未经改进的BP神经网络直接应用时效果常不够理想。目前，研究者对BP神经网络的改进研究通常集中在附加动量项和学习率自适应等方面,如：谢汝兵等[6]对BP神经网络进行了附加动量项改进并应用于机械故障诊断；王莉莉等[7]对BP神经网络进行“动量-学习率自适应”改进后应用于电容层析成像(Electrical Gapacitance Tomography，ECT)流型辨识；陈华珍等[8]提出了附加动量和学习率的自适应算法，并将这种“双自适应”BP神经网络应用于智能手环体征检测。然而，由于上述方法中动量因子和学习率或固定不变,或仅在有限的固定点上变动，自适应功能较弱，网络收敛性仍显不足。笔者将C语言中的“指针”思想引入BP神经网络中，创建了网络“误差指针”。通过“误差指针”对学习率和动量因子进行双自适应调整，进一步扩展了二者的取值空间，有利于网络更深层次的自适应调整，可提高网络收敛速度和诊断精度。

1 典型BP神经网络及改进

1.1 典型BP神经网络

BP神经网络的结构通常有输入层、隐含层和输出层3部分，根据隐含层数量不同，BP神经网络可分为单隐层和多隐层。研究表明:单隐层即可实现任意非线性映射功能。典型的单隐层BP神经网络结构如图1所示。

BP神经网络基本信号传输和调整原理如下：

输入信号

(1)

输出信号

(2)

式中：σ(·)为激活函数。

样本误差

e(n)=L(a[l](n),y)，

(3)

式中:y为期望的输出;L(·)为损失函数。

输出层梯度

(4)

式中：σ′(·)为激活函数的导数。

隐含层梯度

(5)

第n次迭代的偏置

(6)

式中：η为学习率(也称步长)，通常取(0,1)区间内的一个常数。

第n次迭代的权重

(7)

可见，标准BP算法属于简单的最速下降寻优法，其调整方向与梯度方向相反。

1.2 动量-自适应学习率BP神经网络

由于神经网络在修正权值和偏置过程中仅仅考虑了当前时刻的梯度，未考虑前一时刻的变化方向，导致网络在学习过程中容易发生振荡，收敛速度缓慢。因此，有研究者提出通过附加动量项的方式进行改进，改进后偏置和权重修正公式如下：

第n次迭代的偏置为

(8)

式中：μ为动量因子，通常取[0.1,0.8]区间内的一个常数。

第n次迭代的权重为

(9)

为了进一步加速网络收敛，有研究者提出对学习率η进行自适应改进，即η不再取固定值，而根据误差大小进行调整，通常取如下阶梯函数[9]：

(10)

可见，这种学习率自适应调整的基本思路是：误差降低时说明调整方向正确，此时增大学习率加速收敛；误差增大时说明调整方向错误，此时降低学习率避免振荡。使用批量训练方式的动量-学习率自适应BP算法流程如图2所示，其中ep为误差容限。

2 改进的双自适应BP神经网络

前述方法中，虽然通过附加动量项能有效抑制振荡，促进网络收敛，但如何选取动量因子μ一直没有较好的方法。μ选取过小，惯性效果弱，对于网络的振荡抑制不够明显；μ选取过大，惯性效果过于显著，又不易加速收敛。孙瑜[10]通过对比μ取不同值时神经网络收敛效果，得出了μ的最佳值与学习率η有关的结论，并给出了不同η下μ的一些取值范围。但因神经网络初始权值的随机性，其最佳值理论尚不具备一般性。同时，学习率自适应方法仅考虑误差的增大或减小，而未考虑误差连续增大或减小的情况，自适应能力仍显不足。

于海宁等[11]在研究C语言程序设计时提出一种改进的指针分析方法，提高了对敏感量的控制能力。BP神经网络中动量因子和学习率作为对误差函数敏感的变量，同样适用于上述方法。因此，笔者设计了计数器p1(p2)作为网络误差e(n)连续增大(减小)的标志量，并将其作为“误差指针”供动量因子和学习率自适应调节时引用，具体调整策略如下：

误差指针p1和p2分别为

(11)

(12)

自适应学习率η为

(13)

自适应动量因子μ为

(14)

如：误差e(n)连续减小k次时，说明调整方向正确并且搜索步长不足，此时以k幂指数方式提高学习率η，并以k幂指数方式降低动量因子μ，这样就可以进一步加速网络收敛。使用批量训练方式，改进的双自适应BP算法流程如图3所示。

3 仿真实验及结果分析

实验分析程序运行于Windows10系统，处理器为Intel(R)Core(TM)i5-7200u，CPU 2.50 GHz 2.71 GHz，软件版本为MATLAB R2016a。

3.1 样本数据

绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor，IGBT)是一种常用的电力电子元件，广泛应用于整流、逆变、脉宽调制等电路。笔者以某型雷达的三相电压型交-直-交变频器逆变电路为研究对象，对其IGBT开路故障进行诊断，其电路如图4所示。

统计表明：三相电压型交-直-交变频器逆变电路中1个IGBT开路故障居多，2个IGBT同时开路故障较少，3个以上IGBT同时故障的概率极小。因此，笔者以单IGBT开路、双IGBT开路(以T3、T4为例)和无故障等状态为诊断内容，对不同状态进行二进制编码并设定了故障编号；通过Simulink获取了IGBT在不同状态下的电路输出电压值，共取得880组样本[12](其中110组为正常值)；随机选取其中的800组用于训练，另外80组用于测试。三相逆变电路IGBT开路故障数据(归一化后)如表1所示。

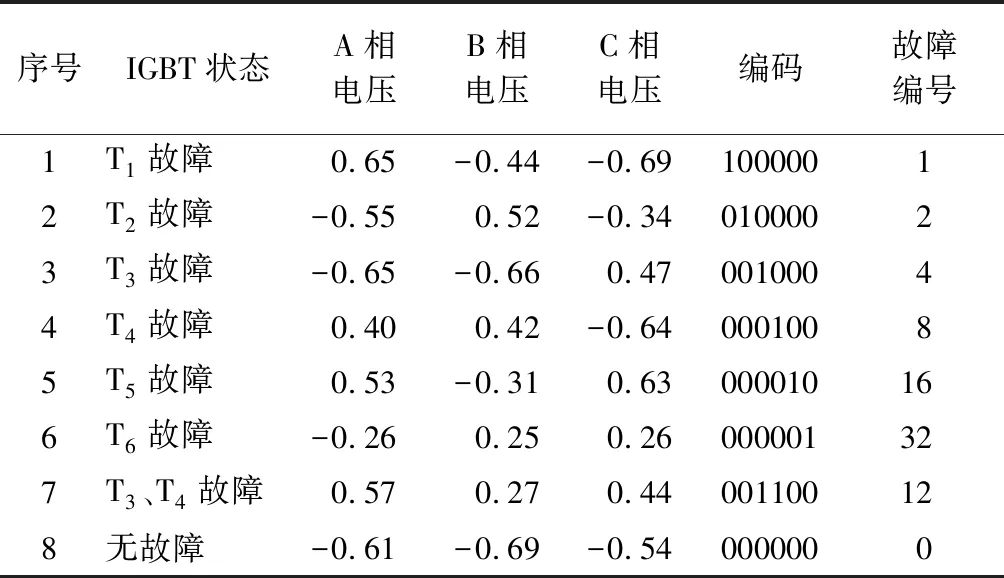
表1 三相逆变电路IGBT开路故障数据(归一化)

3.2 故障诊断方法对比

根据样本特点，设计了3×5×6的BP神经网络，使用批量训练方式。其中隐层传输函数为Log-sigmoid，输出层传输函数为Purelin。最大迭代次数为300步，为了更好地对比各算法收敛性，误差容限设为0。

当使用典型BP神经网络进行故障诊断时，选取的学习率和动量因子不同，网络收敛也不同。经测试，学习率η和动量因子μ分别选取0.8和0.7时，神经网络学习效果最理想，达到稳定误差的迭代次数132步。使用训练好的网络进行测试，诊断正确率为75%，误差曲线及诊断结果见图5、6。

由式(3)、(7)，可得典型BP神经网络的误差为

(15)

在使用动量-自适应学习率调整方法时，学习率初始值设置为0.8。经验证，μ=0.6时，神经网络学习效果最理想，达到稳定的迭代次数为38步，测试准确率提高至76.25%，误差曲线及诊断结果如图7、8所示。

由式(3)、(9)，可得动量-自适应学习率的网络误差为

(16)

最后，使用基于误差指针改进的学习率和动量因子双自适应性BP算法，学习率初始值同样取0.8，动量因子初始值取0.6。此时，网络达到稳定的迭代次数为46步，准确率为82.5%。误差曲线及诊断结果如图9、10所示。

由式(3)、(13)、(14),可得改进的双自适应神经网络误差为

(17)

此时，误差e(n)受η(n-1)和μ(n-1)双重调节，在指针变量p1(p2)的控制下，误差正常下降时，调节速度不断加快，出现震荡时，调节幅度时将得到抑制。因此，其误差降低速度加快，并且振荡效果得到了较好的抑制。

为了进一步对比各种算法，取网络最后100次迭代误差进行对比，结果如图11所示。不同算法误差均值分别为0.685、0.390、0.308，均方差分别为0.002 40、0.001 30、0.000 12，由此可知：经改进的双自适应BP算法收敛性和诊断精度均优于典型BP算法和动量-自适应学习率BP算法。

4 结论

笔者通过建立误差指针，设计了基于改进双自适应的BP算法，并建立了相应故障诊断模型。仿真实验证明该方法既增强了网络的收敛性，又提高了故障诊断精度，可以改善现有方法收敛速度慢、不稳定、诊断精度偏低等缺陷。但本文并未对动量因子、学习率初始值和调整门限的选取进行研究，而初始值和调整门限的取值在一定程度上影响BP神经网络的性能，因此，需对相关内容做进一步研究。