混凝土类材料SHPB 实验中确定应变率的方法*

胡亮亮，黄瑞源,，高光发，蒋 东，李永池

（1. 南京理工大学瞬态物理国家重点实验室，江苏 南京 210094；

2. 中国科学技术大学近代力学系，安徽 合肥 230027；

3. 北京航天长征飞行器研究所，北京 100076）

混凝土类材料已被广泛应用于民用建筑及防御工事[1-3]，它在爆炸冲击载荷作用下的动态力学性能和破坏机理，对于民用建筑及防御工事的设计和防护具有重要指导意义[4-6]，目前一般采用SHPB 技术来研究不同应变率下混凝土类材料的动态力学性能[7-9]。混凝土作为一种脆性材料，其破坏应变非常小，通常只有千分之几，而动态力学性能实验的加载时间又非常短，产生的高应变率往往会引起试件的结构破坏而非材料破坏，从而对SHPB 技术在混凝土材料中的应用提出了挑战[10-12]。Frew 等[13]针对波形整形技术，在脆性材料SHPB 实验中的应用展开研究, 认为应力均匀性问题相对比较容易解决, 同时指出恒应变率加载却很难实现。卢玉斌等[14]对于脆性材料SHPB 实验中实现近似恒应变率加载的必要性进行了讨论，认为恒应变率加载实现难度较大。陶俊林等[15]提出了两种SHPB 方法来实现对金属材料的恒应变率加载，但对于混凝土等脆性材料仍很难实现恒应变率加载。周子龙等[16]认为加载应力和试样应力历程具有相同的变化规律时，试样变形将处于恒应变率状态，但是对于如何实现恒应变率加载并没有给出明确的方法。由于在SHPB 实验中很难实现混凝土试件的恒应变率加载[17-19]，部分学者通过采用变截面杆[20]、波形整形技术[21-22]以及异形冲头法[23]等对输入波形进行了优化，从而实现了中低应变率下的恒应变率加载，但是目前已有的方法仍很难实现混凝土试件在较高应变率下的恒应变率加载。因此，如何处理非恒应变率加载下的实验数据，并确定其对应的应变率，就成为了一个迫切需要解决的问题。

为了确定混凝土类材料在SHPB 实验中所对应的应变率，本文中对3 种不同强度和4 种不同钢纤维含量的混凝土试件进行SHPB 实验，并针对实验得到的30 组恒应变率加载下的实验数据进行归纳总结，探索一种混凝土类材料SHPB 实验中确定应变率的方法，拟为处理非恒应变率加载下的实验数据并确定其对应的应变率提供合理的解决方法。

1 试 件

试件为3 种不同强度和4 种不同钢纤维含量的混凝土。3 种不同强度混凝土材料配比见表1，利用设计模具浇铸，尺寸为 70 mm×35 mm。试件养护过程符合工程要求，并利用磨床对两端面进行研磨，其不平行度在0.02 mm 以内，试件最终长径误差在±0.02 mm。4 种不同钢纤维含量混凝土试件的制作采用二次合成法工艺，基体强度为C40，坍落度为160～200 mm。采用 70 mm×35 mm 的圆柱钢模浇筑并振动成型，拆模后，室温条件标准养护28 d，实验时混凝土龄期为80 d 以上。钢纤维采用0213 型微钢纤，纤维直径d=0.2 mm、长度l=13 mm（特征比l/d=65，外形平直光洁）。钢纤维混凝土的实际配合比见表2。

表 1 不同强度混凝土试件配合比Table 1 Mixture ratio of concrete specimen with different strengths

表 2 不同钢纤维含量混凝土试件配合比Table 2 Mixture ratio of steel fiber reinforced concrete specimen

2 实 验

实验在 74 mm 的SHPB 实验装置上完成，实验装置如图1 所示。通过贴在入射杆和投射杆中部的应变片采集入射波εi、反射波εr和透射波εt，计算试样的动态平均应力σ、应变ε 和应变率：式中：c0为压杆的弹性波速，L 为试件的长度，A 为压杆的横截面积，As为试件的横截面积，E 为压杆的弹性模量。

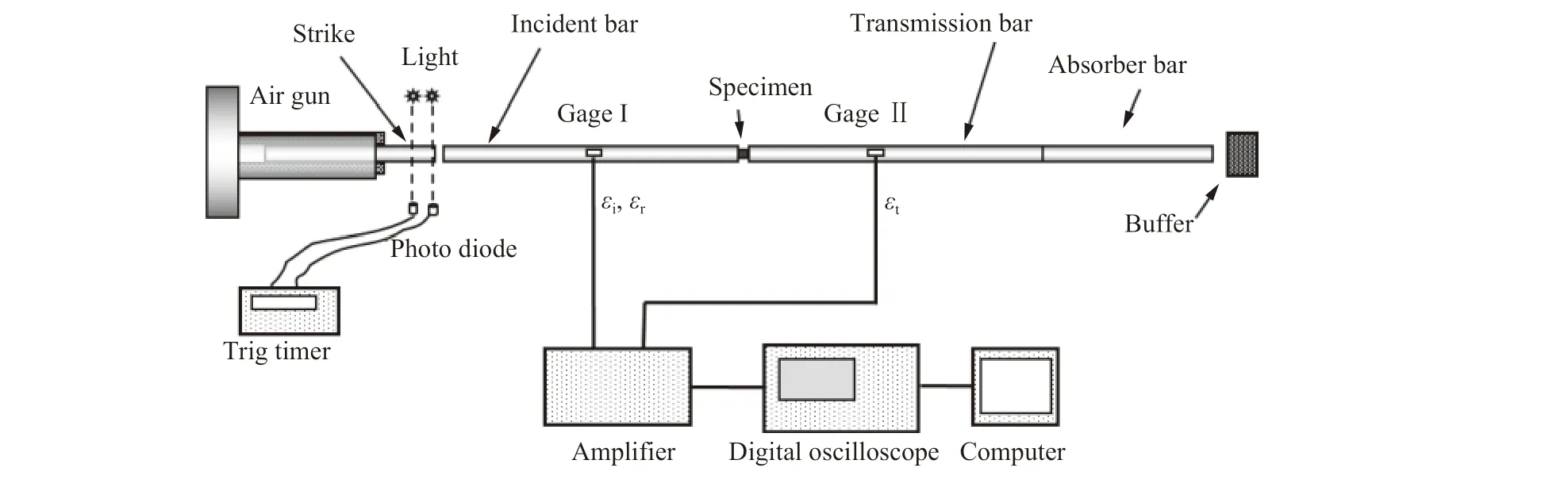
图 1 实验装置Fig. 1 Experimental device

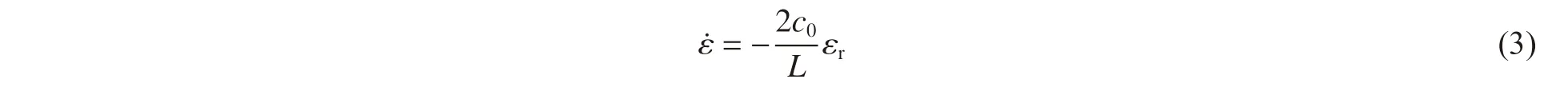
由式（3）可知，试样变形的应变率由反射应力波确定，即应变率和反射波波形呈线性关系，因此在SHPB 实验中实现恒应变率加载可以由在有效加载时间内在反射应力波上得到的一个近似恒定平台表征[24]。

3 恒应变率加载

选取直径20 mm、厚度1.0～2.5 mm 的黄铜材料作为波形整形器。为了得到恒应变率加载的实验数据，通过采用不同几何尺寸的黄铜波形整形器对不同强度（C20，C45，C70）和不同钢纤维含量（0%，0.75%，1.50%，4.50%）的混凝土进行了大量SHPB 实验，获得的典型波形如图2 所示。

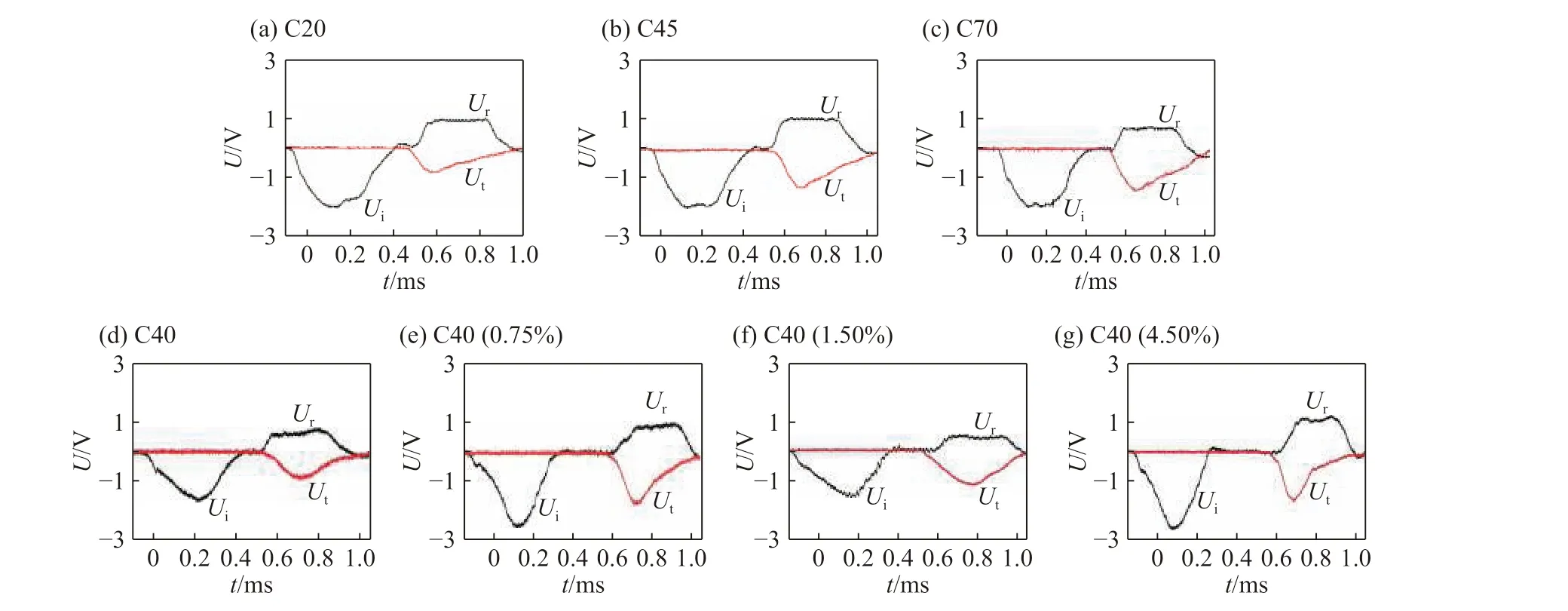
图 2 不同强度和不同钢纤维含量的混凝土材料的典型波形Fig. 2 Typical waveforms for concrete-like materials with different strengths and different fiber contents

SHPB 实验主要基于两个基本假定：一维假定和均匀性假定。Ravichandran 等[25]认为应力波在试件中传播3 个来回，试件可近似达到应力均匀状态。3 个来回的时间为Δt=6L/c，波速 ，ρ 为试件的密度。以图2（b）中C45 混凝土的典型波形为例，对应力与应变率曲线进行分析，其中L=35 mm、E=33.5 GPa、ρ=2 530 kg/m3，经计算波速c=3 700 m/s，Δt=57 μs，即试件在57 μs 的时候已经达到应力均匀状态, 而此时对应的应力还不到峰值应力的15%。由图3 可以看出，反射波脉冲上升沿作用时间为92 μs，即试件达到恒应变率加载段需要的时间为92 μs，该时刻对应的应力为峰值应力的50%，说明通过黄铜整形器得到的实验数据实现了混凝土材料的恒应变率加载并满足加载过程中的应力均匀性假定。图4 分别给出了30 组恒应变率实验数据中C20、C70 和C40 (0.75%)混凝土试件在相近恒应变率加载下的应力应变曲线对比，从图中可以看出，实验数据重复性较好。

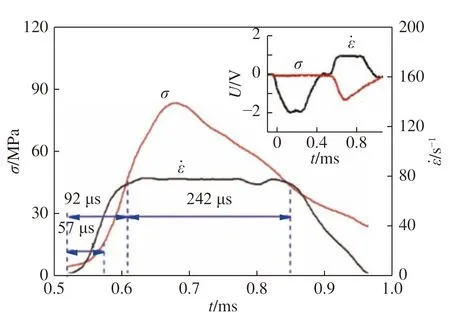
图 3 典型的应力曲线与应变率曲线Fig. 3 Typical stress curves and strain rate curves

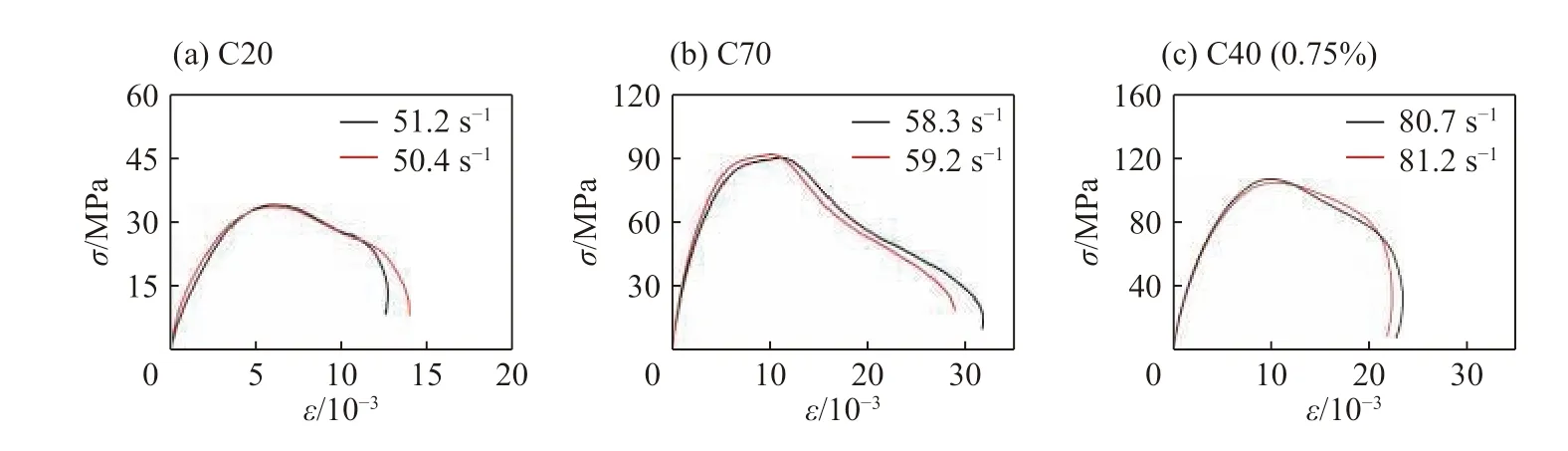
图 4 相近恒应变率加载下的应力应变曲线对比Fig. 4 Comparison of stress-strain curves under similar constant strain rate loading

4 非恒应变率加载下实验数据修正系数的提出

由于SHPB 实验中很难实现混凝土类材料的恒应变率加载，非恒应变率加载下的实验数据居多。为了处理非恒应变率加载下的实验数据，陶俊林等[26]采用应变率时程曲线的算数平均值来表征恒应变率；李为民等[27]采用应变率时程曲线的波头至应力峰值之间的算数平均值来表征恒应变率；Wang 等[28]认为，应变率时程曲线可以取80%至峰值应变率之间为恒应变率加载段。确定应变率方法的不同，将导致同一组实验数据所对应的应变率的确定具有较强的主观性，从而为研究混凝土类材料的应变率效应带来误差，因此如何合理地确定混凝土类材料SHPB 实验中的应变率尤为重要。

下面，将通过使用不同应变率选取方法来处理恒应变率加载下的实验数据，通过对比不同选取方法得到的应变率数值，探寻不同确定应变率方法之间是否存在一定的规律。图5 为其中一组恒应变率加载下的实验数据，其对应的原始波形为图2(b)。如图5 中所示，其实验数据对应的平台段恒应变率为77.3 s-1；半段平均应变率选取的是波头至应力峰值这个时间段内应变率算数平均值，通过计算得到的半段平均应变率为42.2 s-1，整段应变率平均值选取的是曲线波头至波尾这个段曲线内算数平均值，通过计算得到全段平均应变率为56.2 s-1。因此，可得恒应变率/半段平均应变率η1=77.3/42.2=1.832，而恒应变率/全段平均应变率η2=77.3/56.2=1.375。

对30 组恒应变率加载下的应变率曲线进行同样的处理，得到这些曲线对应的恒应变率、半段平均应变率、全段平均应变率，并求得恒应变率/半段平均应变率以及恒应变率/全段平均应变率，见表3。图6 对恒应变率/半段平均应变率和恒应变率/全段平均应变率进行了汇总，从图中可以发现，恒应变率/全段平均应变率基本保持在约1.38，而恒应变率/半段平均应变率浮动比较大，没有一定的规律。

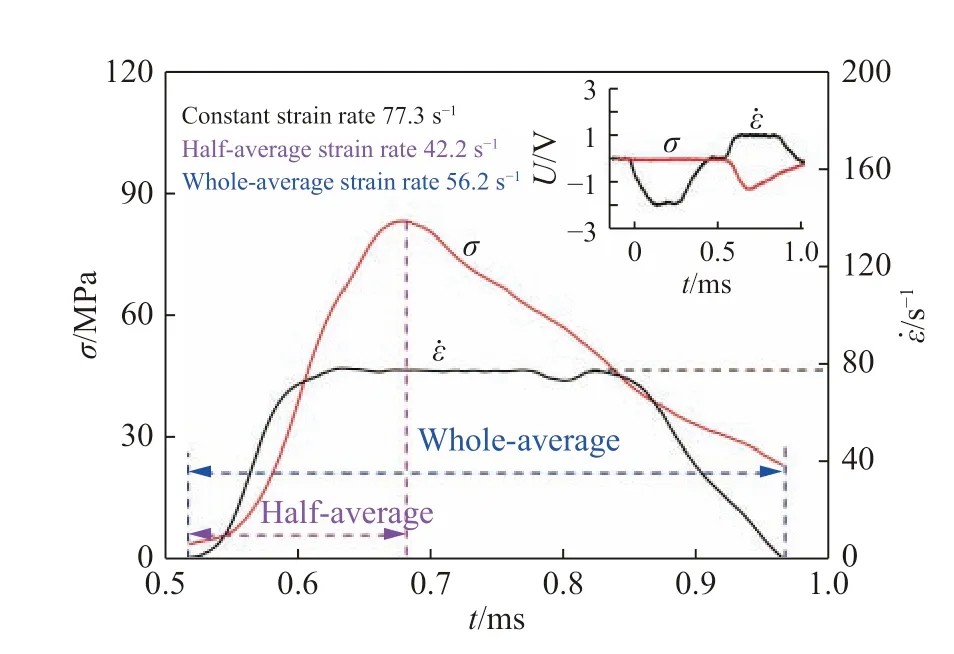
图 5 确定应变率的不同方法Fig. 5 Ways for determining strain rate

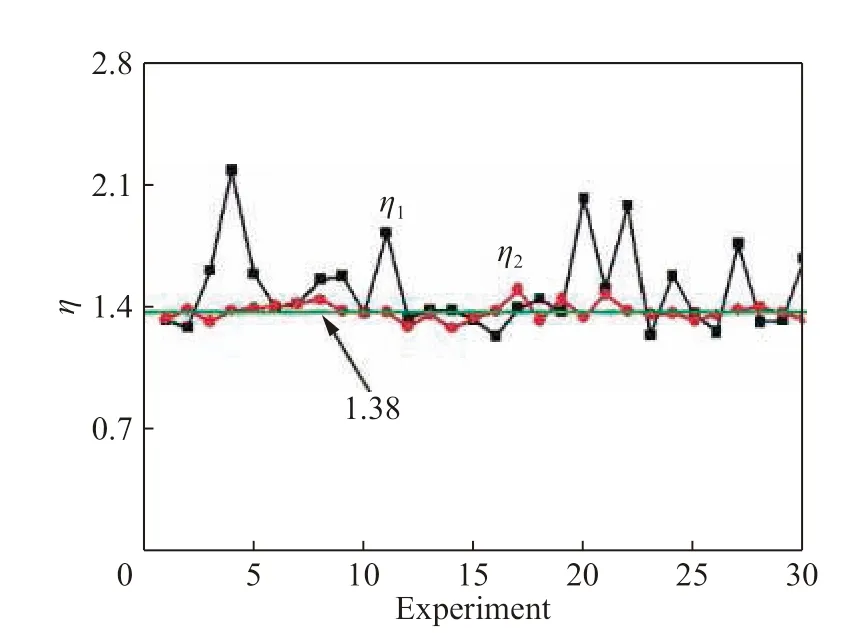
图 6 恒应变率与半段（全段）平均应变率之比Fig. 6 Constant strain rate versus average strain rate of half and whole-stage

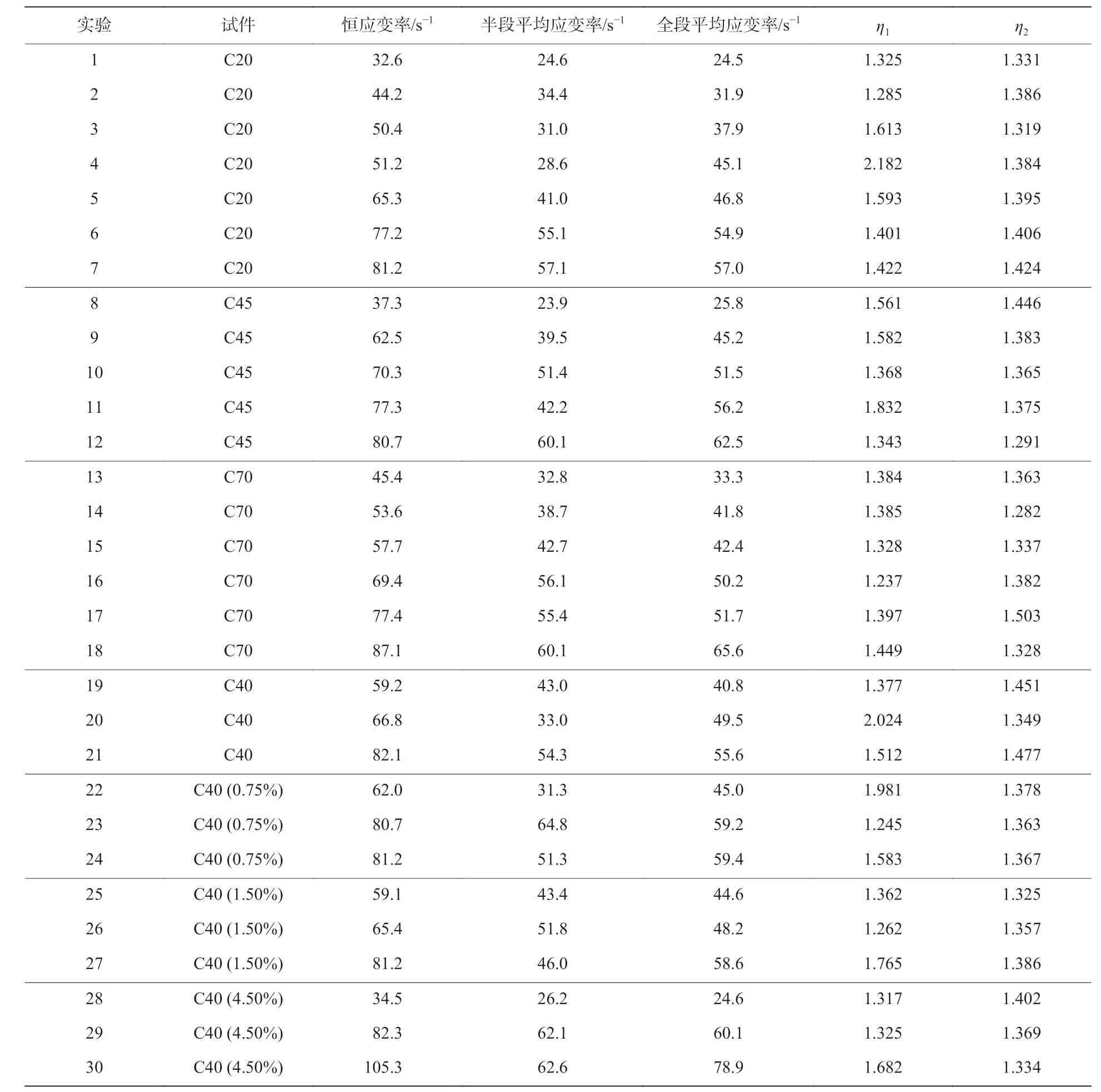
表 3 恒应变率加载下的实验数据Table 3 Experimental data at constant strain rate loading

由此可以得到结论：对于恒应变率加载下的实验数据，其对应的应变率可以采用反射波平台段数值直接得到，也能够采用全段平均应变率乘以系数1.38 来确定，并把全段平均应变率乘以系数1.38 定义为等效应变率。由于把等效应变率确定为实验曲线所对应的应变率的方法是由恒应变率加载下的实验数据得到的，它对于非恒应变率加载下的实验数据是否适用还未进行有效验证。下面对非恒应变率加载下的实验数据采用该确定应变率的方法进行处理，得到该实验数据对应的等效应变率，并与相近数值恒应变率加载下的实验数据进行对比。图7 为恒应变率和非恒应变率加载下的应力应变曲线的对比图，图中右上角为实验数据分别对应的应变率曲线的加载情况。

由图7 可以看出，如果非恒应变率加载下的等效应变率和恒应变率加载下的恒应变率差相近，则两者对应的应力应变曲线重合度比较高。因此，采用全段平均应变率乘以系数1.38 来表示实验数据所对应的等效应变率是完全可行的，并且该方法对于处理不同强度和不同钢纤维含量的混凝土材料在SHPB 实验中的数据都适用。

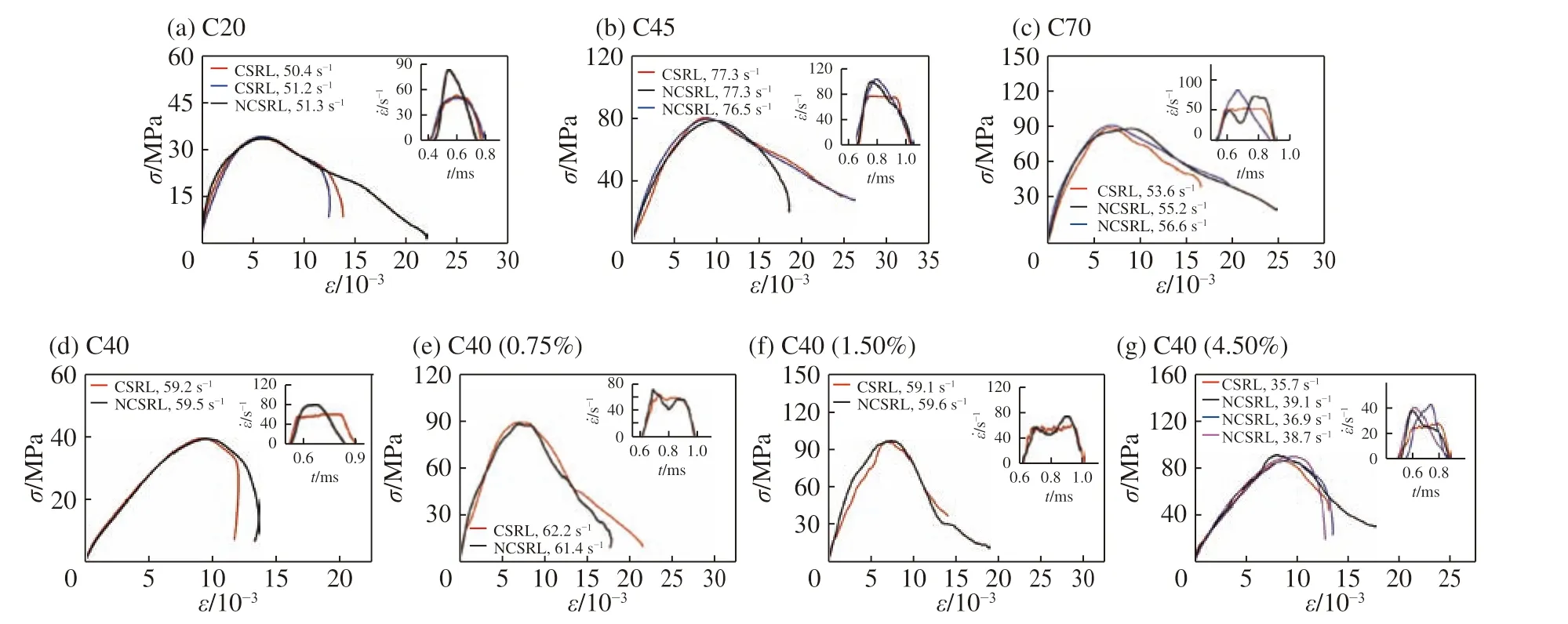
图 7 非恒应变率加载与相近恒应变率加载下的应力应变曲线对比Fig. 7 Comparison of stress-strain curves under non-constant strain rate loading (NCSRL)and similar constant strain rate loading (CSRL)

5 反射波时程曲线平台段较短的实验数据对应应变率的确定

目前，一般认为实验数据的反射波时程曲线存在平台段，即可认为是恒应变率加载，因此Wang 等[28]把反射波时程曲线只有较短平台段的实验数据认为是恒应变率加载的。由于没有对平台段长度到底多长才算恒应变率的相关报道，因此把反射波时程曲线只存在较短平台段的实验数据认为是恒应变率加载的合理性还有待进步一考究。本文中结合前文所得到的方法，对反射波时程曲线只有较短平台段类型的数据进行处理，图8 为C45 混凝土某个反射波时程曲线只有较短平台段类型的一组实验数据的原始波形，其反射波时程曲线的平台段对应的应变率为72.6 s-1，而采用全段平均应变率乘以系数1.38 得到的等效应变率为63.4 s-1。图9 给出了C45 混凝土5 组恒应变率加载下的实验数据，与其进行对比。从图9 可以看出，等效应变率为63.4 s-1的较短平台段类的应力应变曲线与恒应变率为62.5 s-1的实验数据重合度较好，与恒应变率为70.3 s-1的实验数据差异较大。因此，反射波时程曲线平台段较短的实验数据对应应变率不能直接采用平台段对应的应变率来表征，而应该采用本文中提出的全段平均应变率乘以系数1.38 的等效应变率来表征。假如实验数据得到的反射波时程曲线平台段的长度不是太长，那么采用本文中所提的确定应变率的方法会更合理些。

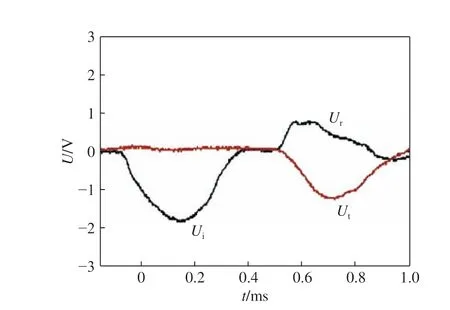
图 8 较短平台段的原始波形Fig. 8 Original waveform of short timeconstant strain rate loading

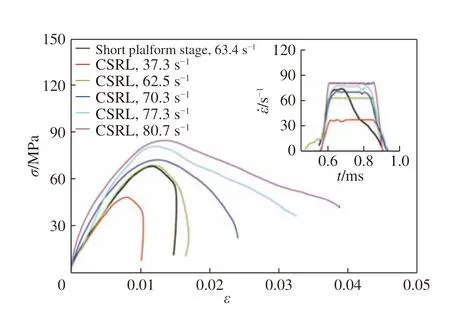
图 9 C45 混凝土在不同加载情况下的应力应变曲线对比Fig. 9 Comparison of stress-strain curves of C45 concreteunder different loading conditions

6 结 论

采用直径20 mm、厚度1.0～2.5 mm 的黄铜材料作为波形整形器，针对不同强度（C20，C45，C70）和不同钢纤维含量（0%，0.75%，1.50%，4.50%）的 70 mm×35 mm 混凝土材料进行了SHPB 实验，得到以下结论。

(1) 通过采用不同尺寸的黄铜材料作为波形整形器，能够得到低应变率下的恒应变率加载实验数据，但是很难得到高应变率下的恒应变率加载实验数据。

(2) 通过对实验得到的30 组恒应变率加载下数据进行归纳总结，提出了混凝土类材料SHPB 实验数据所对应的应变率可以采用全段平均应变率的1.38 倍来表征的确定应变率的方法。

(3) 对比非恒应变率加载下的等效恒应变率和恒应变率加载下的恒应变率的数值相近的实验数据，由于其对应的应力应变曲线重合度非常高，从而表明采用本文中确定应变率的方法对于非恒应变率加载的实验数据是适用的。

(4) 反射波时程曲线平台段较短的实验数据不能视为恒应变率加载，其对应的应变率可以采用本文中确定应变率的方法来确定。