基于安全距离模型的车辆跟随控制策略研究＊

关志伟 丁建峰 闫光辉

（天津职业技术师范大学，天津 300222）

主题词：安全距离模型 BP神经网络PID控制器 缩微智能车 车间距误差

1 前言

当前，智能交通行业迅速发展，车路协同控制技术逐渐成为研究热点[1]，作为能有效消除驾驶员不稳定性因素、提高道路通行效率的解决方案而备受关注。纵向控制是车路协同研究领域中的典型技术，国内外学者也先后提出相关控制方法和设计方案。Wang Yuejian等人[2]设计了一种基于滑模控制（Sliding Mode Control，SMC）的模型匹配控制（Model Matching Control，MMC）方案，用于实现车辆跟随的速度控制，该方案还建立了车辆加速度控制的传递函数和基于滑模控制反馈的模型匹配控制器；Payman Shakouri等人[3]设计了一种利用单个控制回路的控制方案，通过引入与前、后车辆之间的相对距离和前车速度相对应的额外状态变量实现车辆速度和距离的跟踪；张向南基于模糊控制理论对传统的车辆自适应巡航控制算法进行了改进，提出了一种采用模糊控制策略进行智能调节的车辆自适应巡航控制方法[4]。

本文选取车辆跟随过程作为纵向控制的核心应用场景，通过建立安全距离控制模型，设计跟随控制器并利用MATLAB/Simulink软件进行仿真分析，运用缩微环境下的智能车辆系统试验平台完成验证。

2 安全距离控制模型

假设跟随系统采用相同道路上若干车辆组成的具有共同行驶方向且时刻保持安全车间距的行驶方式，该条件下车间纵向安全距离受车辆数量或车队总长的干扰小，车队可稳定行驶。首先，该安全距离模型以纵向控制为基础，能充分反映车辆协同行驶的过程；其次，该模型以相对误差为研究重点，并通过将相对误差作为控制系统的输入，采用智能控制算法减小误差，实现车辆的安全稳定跟随。车间纵向相对距离如图1所示。

图1 车间纵向相对距离示意

由图1，车间纵向相对距离误差为：

式中，Δxi为第i辆车与第(i+1)辆车的实际车间距；ds为各车辆间的期望车间距。

鉴于跟随车辆的速度会对数学模型精度产生一定影响，将式（1）进行优化，得到更高精度的相对距离误差表达式：

式中，δd为考虑跟随车速度的车间纵向相对距离误差；vi+1为跟随车速度；λ为跟随车δd收敛于δd1的补偿时间，一般选取λ=0.2 s。

而车间纵向相对速度误差可表示为：

式中，vi为巡航车速度。

现以上述关系式为核心，建立基于前、后车的车间纵向安全距离模型，其状态空间表达形式为：

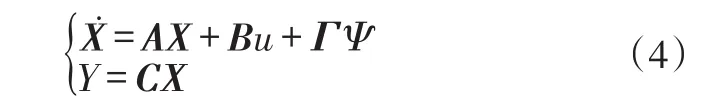
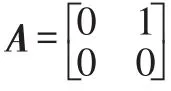
车间纵向安全距离模型中选取δd和δv作为状态变量，用于评价车辆跟随过程的控制效果，由于本文利用仿真和试验验证BP神经网络PID控制器对跟随系统中安全车间距的控制效果，根据BP神经网络输入层的结构特点，仅采用相对距离误差δd这一状态量进行评价分析。

3 BP神经网络PID控制器设计及仿真

3.1 控制器设计

为了使PID控制取得良好的控制效果，必须调整好比例、积分和微分控制的作用[5]，形成控制量中既相互配合又相互制约的关系。神经网络具有逼近任意非线性函数的能力[6]，可以实现并行协同处理，而且自学习能力强，能够通过对系统性能的学习实现最佳组合的PID控制。而BP神经网络学习算法是一种利用梯度最速下降法的算法，其中心思想是通过调整权值使网络的总误差最小化，即采用梯度搜索技术，使网络的期望输出值与实际输出值的误差最小。

因此，本文采用BP神经网络PID控制实现参数Kp、Ki、Kd的自学习和自行调整。BP神经网络PID控制器的结构如图2所示。

图2 BP神经网络PID控制器结构框

本文设计的BP神经网络PID控制器采用如图3所示的3层BP神经网络结构形式，包含1个输入层、1个隐含层、1个输出层。具体来说，控制器采用3-5-3的BP神经网络结构，即输入层的信号为输入量rin、输出量yout和偏差量error，输出层的信号分别为PID控制器的参数Kp、Ki、Kd。

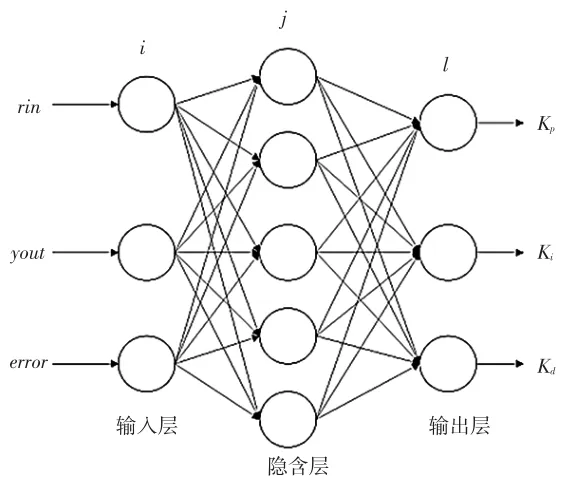
图3 3层BP神经网络结构

3.1.1 工作信号的前向算法

对3层BP神经网络的输入层和隐含层进行逐级分析，得到输出层的输入与输出分别为：

3.1.2 误差信号的反向算法

利用梯度最速下降法对网络的加权系数进行修正，并附加惯性项使得搜索可以快速收敛到全局极小，根据输出层加权系数变化量与系统性能指标函数之间的关系，推导得：

式中，E()为系统性能指标函数；y()为系统性能指标函数的输出量；u()为控制函数。

由式（5）和增量式PID控制表达式[7]推导可得：

式中，e()为误差函数。

综上，输出层加权系数的学习算法为：

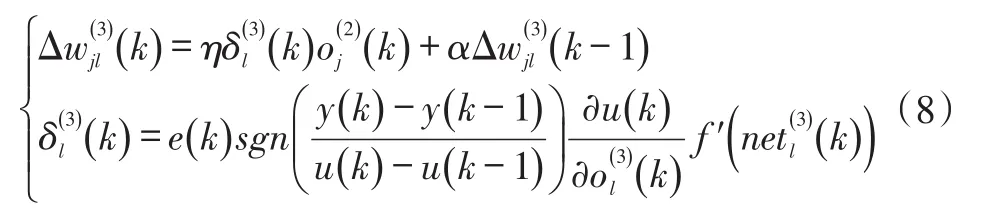
同理，隐含层加权系数的学习算法为：

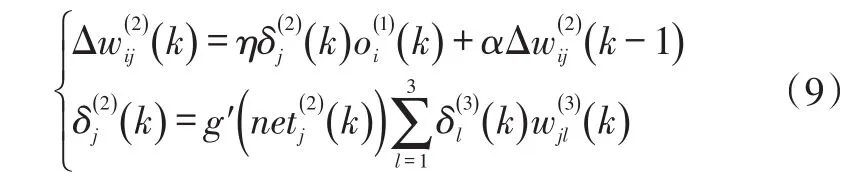
上述BP神经网络PID控制器控制算法流程如图4所示。

图4 BP神经网络PID控制算法流程

3.2 仿真分析

为比较传统PID控制器和BP神经网络PID控制器对跟随系统中安全车间距的控制效果，将式（4）转换为传递函数形式：G(s)=(0.2s+1)/s2。另外，仿真车速取为40 km/h，目标车间距为3 m，车辆基本参数如表1所示。

表1 车辆基本参数

设η=0.25，α=0.01[8]，wij、wjl的初值在区间[-0.5,0.5]上取随机值，传统PID控制的参数分别为Kp=0.85、Ki=0.2、Kd=0.3，仿真采样时间ts=1 s，搭建仿真模型如图5所示。

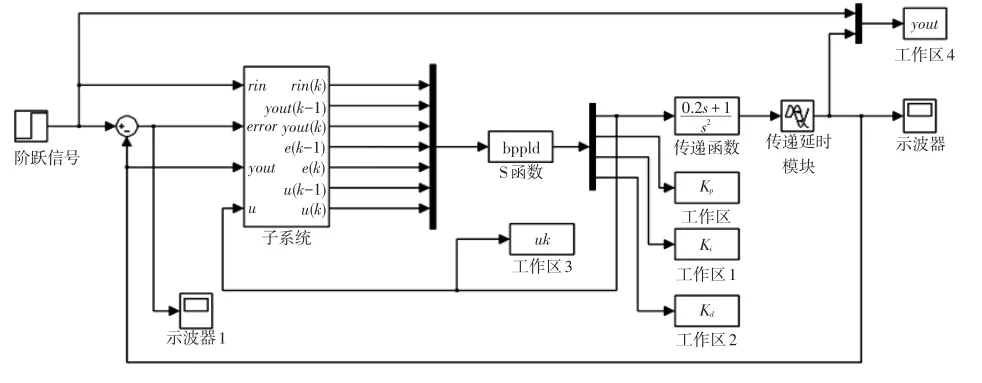
图5 控制仿真模型

在图5所示的控制仿真模型中，将已设计完成的基于BP神经网络的PID控制算法的m文件导入S函数（SFunction）的模块中，并将模块名称设置为“bppid”，仿真时间设定为120 s。

通过对BP神经网络各层加权系数的调整，获得BP神经网络输出层输出的3个参数的变化曲线如图6所示，相对距离误差仿真结果如图7所示。

图6 PID控制器3个参数的变化曲线

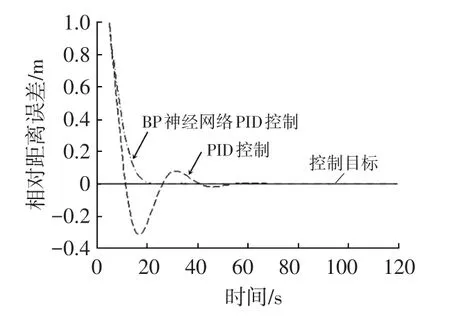
图7 车间纵向相对距离误差仿真结果

由图6和图7可知，采用BP神经网络的PID自适应控制，通过对神经网络各层加权系数的调整，使得BP神经网络PID控制器相对于传统PID控制器的控制准确性明显提升，误差收敛至零的时间明显缩短，且变化非常平稳。仿真结果体现了神经网络算法极强的自学习能力，表明神经网络算法能更快速地使控制系统的实际输出达到期望目标，使控制更精准和高效。

4 缩微环境下的跟随试验

为了更充分地验证智能车跟随系统基于安全距离模型控制器的正确性和可行性，本文利用车-路协同缩微智能车辆仿真试验平台进行车队跟随试验。

4.1 缩微环境下试验平台搭建

缩微环境下智能车试验系统总体框架如图8所示，试验硬件包括缩微道路环境、缩微智能车和多媒体监控系统，软件系统包括视觉模块、控制模块、通信模块和定位模块。各软、硬件之间通过无线网络进行信息交换。

图8 试验系统的总体构架

4.2 缩微智能车跟随试验

4.2.1 试验Update算法

试验Update算法流程为：

a.完成摄像头标定工作[9]；

b.通过主程序读取超声波测距数据，更新前方车辆或障碍物的距离；

c.读取车辆位置信息，判断是否为上、下坡或交叉口路段；

d.读取车道信息，更新转角偏移量；

e.决策并更新电机速度状态和运行状态；

f.决策执行，更新车速和舵机转角，输出至Arduino板通信模块中的ArduinoClient，同时，ArduinoClient输出传感器数据反向传递供主程序读取ArduinoServer，主控模块算法如图9所示。

智能小车的跟随控制过程算法如图10所示。本文利用相对距离误差验证跟随控制器的有效性，因此需要超声波传感器测出实际车间距。采用数字信号处理器（Digital Signal Processor，DSP）上的脉冲宽度调制（Pulse Width Modulation，PWM）功能，向超声波传感器提供10 μs的触发信号，通过如图11所示的数据采集算法得到实际车间距。

图9 主控模块算法

图11 超声波传感器数据采集算法

4.2.2 跟随行驶试验及结果分析

智能车跟随试验在缩微道路环境系统中进行，试验用缩微车有3辆，试验过程如图12所示。

图12 跟随行驶过程

试验过程中，车辆分别在传统PID控制和BP神经网络PID控制下行驶，首车车速设定为50 cm/s，车队中相邻车辆之间的距离目标值设定为40 cm，车队沿着车道线在沙盘路面上跟随行驶。通过数据采集和处理，得到一定试验时间内的相邻两车实际车间距及其误差，分别如图13、图14所示。

图13 实际车间距

图14 车间距误差

通过对试验结果的分析可知：在传统PID控制下，实际车间距偏大，相对车间距误差的波动量较大，车辆可以较稳定地实现跟随行驶；在BP神经网络PID控制下，实际车间距与期望车间距基本吻合，相对车间距误差在趋于零的很小范围内。试验结果说明基于安全距离模型的BP神经网络PID控制器在缩微智能车队跟随行驶过程中达到了预期控制目标。

5 结束语

本文以车辆跟随过程的控制策略为研究重点，建立了车间纵向安全距离控制模型，为了使车间距误差降至最低，实现车辆跟随的稳定控制，将BP神经网络与PID控制相结合，充分利用BP神经网络可以实现误差向后传播的同时修正加权系数的优点，设计了控制器，并给出了相应的控制算法。为验证该控制器的控制效果，分别进行了MATLAB/Simulink仿真和缩微环境下的跟随试验，仿真和试验结果表明，BP神经网络PID控制器的控制准确性较传统PID控制器更高，可满足车辆的安全跟随行驶。由于缩微道路环境的局限性，很多复杂场景未能模拟，后续研究将开展实车测试，在特定的真实道路环境下进行更多协同控制新技术的开发。