基于经验模态分解方法和信息熵的水沙关系研究
张金萍,肖宏林,张 鑫
(郑州大学水利与环境学院,河南 郑州 450001)
黄河以泥沙多而闻名,因泥沙淤积造成的黄河水患给国家和人民造成了极大危害。因此,研究黄河径流-泥沙关系及其演化特征具有重要的意义。胥维坤[1]运用统计学方法分析了小浪底水库运行后对黄河下游水沙变化的影响。方怒放[2]把三峡水利枢纽中的王家桥小流域作为研究区,利用多元相关分析和逐步回归分析研究了降雨、径流、泥沙三者之间对应的关系性。吴敬东等[3]建立了小流域坡面不同治理措施下的径流量与降雨量、降雨历时之间的数学模型,确定了径流量和输沙量之间的关系。河川水沙常常受多种水文因素的影响,在不同时间尺度下呈现复杂的波动特征和关系特性,因此对水沙研究应包含时序多时间尺度细部演化特征分析[4]。本文针对流域产汇流系统在多时间尺度下的径流-泥沙关系,通过经验模态分解(empirical mode decomposition, EMD)方法分析其原始序列的细部演变规律和特征,同时结合信息熵理论,辨识河流水沙关系及其演化特征。
1 数据来源及研究方法
1.1 数据来源
潼关水文站位于黄河中游,是黄河上第二大水文站,潼关断面在黄河、北洛河、渭河3条河流汇流下游不远处,洪水常常在这里相遇,洪水此消彼长,水沙条件复杂。本研究获取了潼关水文站1919—2015年实测径流量和输沙量资料作为研究数据。潼关水文站地理位置和研究时段内的年径流量、输沙量原始序列分别见图1、图2。
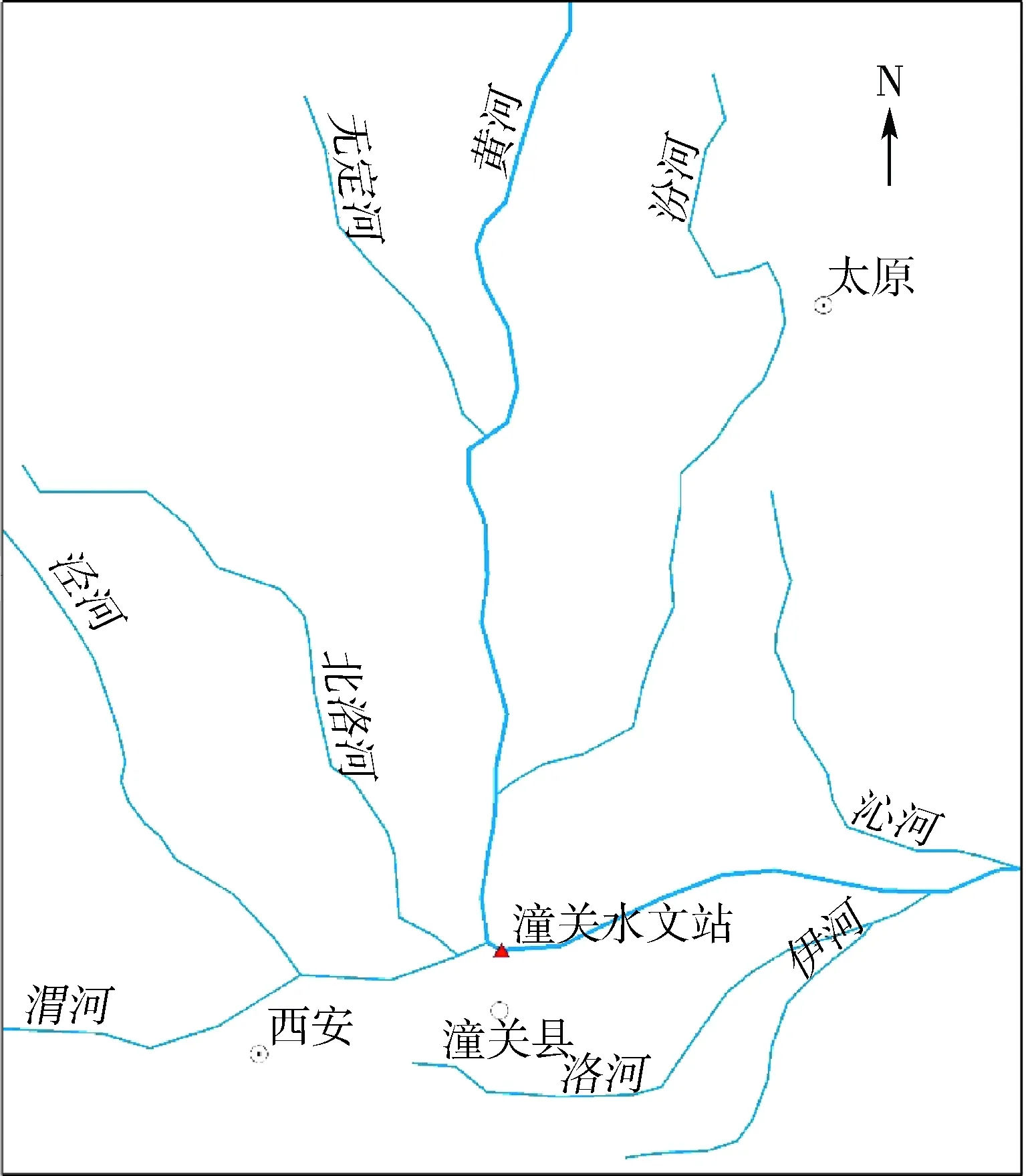
图1 潼关水文站地理位置
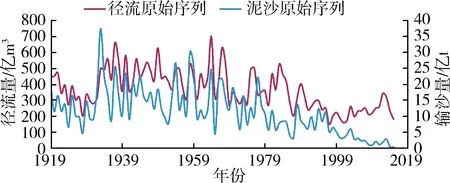
图2 径流、泥沙原始序列
1.2 研究方法
1.2.1EMD方法
EMD方法是Huang等[5]于1998年提出的一种新型自适应信号时频分析方法,近年来在水文水资源领域广泛应用[6]。该方法是通过一个“筛选”过程从被分析原始信号中分离本征模函数(intrinsic mode function, IMF),并且提取的IMF分量需要满足以下条件:①在整个时段内包含所有数据信息的集合中,其数据极大值点与极小值点的数量必须等于经过0点的数量或者数量差值为一个;②在任何时刻,其数据的极大值点连接形成的包络线与极小值点连接形成的包络线的总体均值最终为0[7]。对于复杂信号若不满足IMF所要求的条件,可以利用EMD方法按照分解的步骤对复杂信号进行分解形成一系列满足条件的IMF分量[8]。EMD方法的步骤为:
步骤1:首先定义一个原始信号为X(t)。
步骤2:分析原始信号X(t)找出它全部的极大值点与极小值点及其对应位置,并利用插值方法处理形成上下包络线,求出极大值点和极小值点形成的包络线的均值M1和原始信号X(t)与均值M1之间的差值H1,即H1=X(t)-M1。若H1满足IMF的两个条件,则进行步骤4,否则进行步骤3。
步骤3:把H1看作原始信号重复步骤2求得上下包络线形成的均值M2,再通过上述方法计算出差值H2,并判断其是否满足IMF的条件,若还不满足继续重复直至找到满足IMF条件的分量。
步骤4:将第一个IMF分量从X(t)中分离,从而得到R1,即R1=X(t)-H1。
步骤5:重新把分离后的差值R1看作原始信号并重复步骤2~4得到n个满足条件的IMF分量和1个趋势项(residual, RES)分量Rn,从而完成对原始信号的分解过程。
通过以上步骤可将潼关水文站径流量、输沙量进行EMD分解,提取多个IMF分量。
1.2.2信息熵理论
Shannon[9]参考热力学上的知识,把信息熵定义为排除了信息冗余后的平均信息量。若系统变量有U1,U2,…,Un共n种取值,对应概率分别为:P1,P2,…,Pn且各种取值的出现彼此独立,此时信源的平均不确定性应为每个符号不确定性-lnPi统计得到的数学期望称为信息熵[10-11]。信息熵H(U)的计算公式为
(1)
信息论中用信息熵来表示系统本身所拥有信息量的多少。一个系统表现得越稳定、越有规律,则该系统对应的信息熵值就越小,所以信息熵也用来表示系统的稳定性程度、有序化程度[12-13]。
互信息在信息论中表示两变量之间的相关性,它反映随机变量之间共有的信息量或相互间的依赖关系[14]。若两随机变量间的联系越紧密,则它们的互信息熵值就越大,同理在相反情况下,则两者之间的互信息熵值就越小[15]。
分别计算径流、泥沙原序列及分解后的IMF分量的信息熵,并通过计算径流、泥沙的互信息从而确定黄河流域径流-泥沙的关系。以潼关水文站实测径流量或输沙量为例,设原始信号X(t)为潼关水文站1919—2015年径流量或输沙量数据,经EMD分解可得到n个不同的IMF分量,每个分量包含m年的实测分解值。则得有判定矩阵:
C=(Cst)n×m(s=1,2,…,n;t=1,2,…,m)
(2)
式中Cst为第s个IMF分量的第t年的实测分解值。
为了排除干扰,在计算各IMF分量的信息熵时,首先需要对n个IMF分量的所有数据作归一化处理。得到归一化矩阵B,归一化处理公式为
(3)
式中:Bst为B的元素;Cmax、Cmin分别为同一IMF分量系列数据的最大值和最小值。
将区间[0,1]平均分成L组,每组长度为1/L,对应的区间为[0,1/L),[1/L,2/L),…,[L-1/L,1]。对于某个IMF分量m年归一化数据中第t年在相应的某个分组区间内的概率Pl为t/m[16]。由信息熵的定义和计算公式知,为保证lnPl始终有意义,需要对Pl进行修正,即当Pl为0时假设lnPl为0。则第s个IMF分量的信息熵为
(4)
根据式(4)可依次求出经EMD分解的IMF分量信息熵值,同理求得趋势项的信息熵值。在此基础上,利用式(5)求出它们之间的互信息熵,得出相互间的关联度。
MI(a,b)=H(a)+H(b)-H(a,b)
(5)
式中:MI(a,b)为互信息熵值;H(a)、H(b)分别为径流量、输沙量各分量的信息熵;H(a,b)为二者对应各分量之间的联合熵。
2 结果分析
2.1 EMD方法分析
应用前文EMD分解步骤对潼关水文站1919—2015年径流量、输沙量原始序列进行分解,分别得到径流量和输沙量的4个IMF分量与1个RES分量。径流量、输沙量各分量序列见图3。
由图3可知,径流量和输沙量均包含着复杂得多时间尺度周期性变化和宏观趋势走向。径流量和输沙量IMF1分量对应的准周期约为5 a和4 a,IMF2分量的准周期约为8 a和6 a,IMF3分量的准周期约
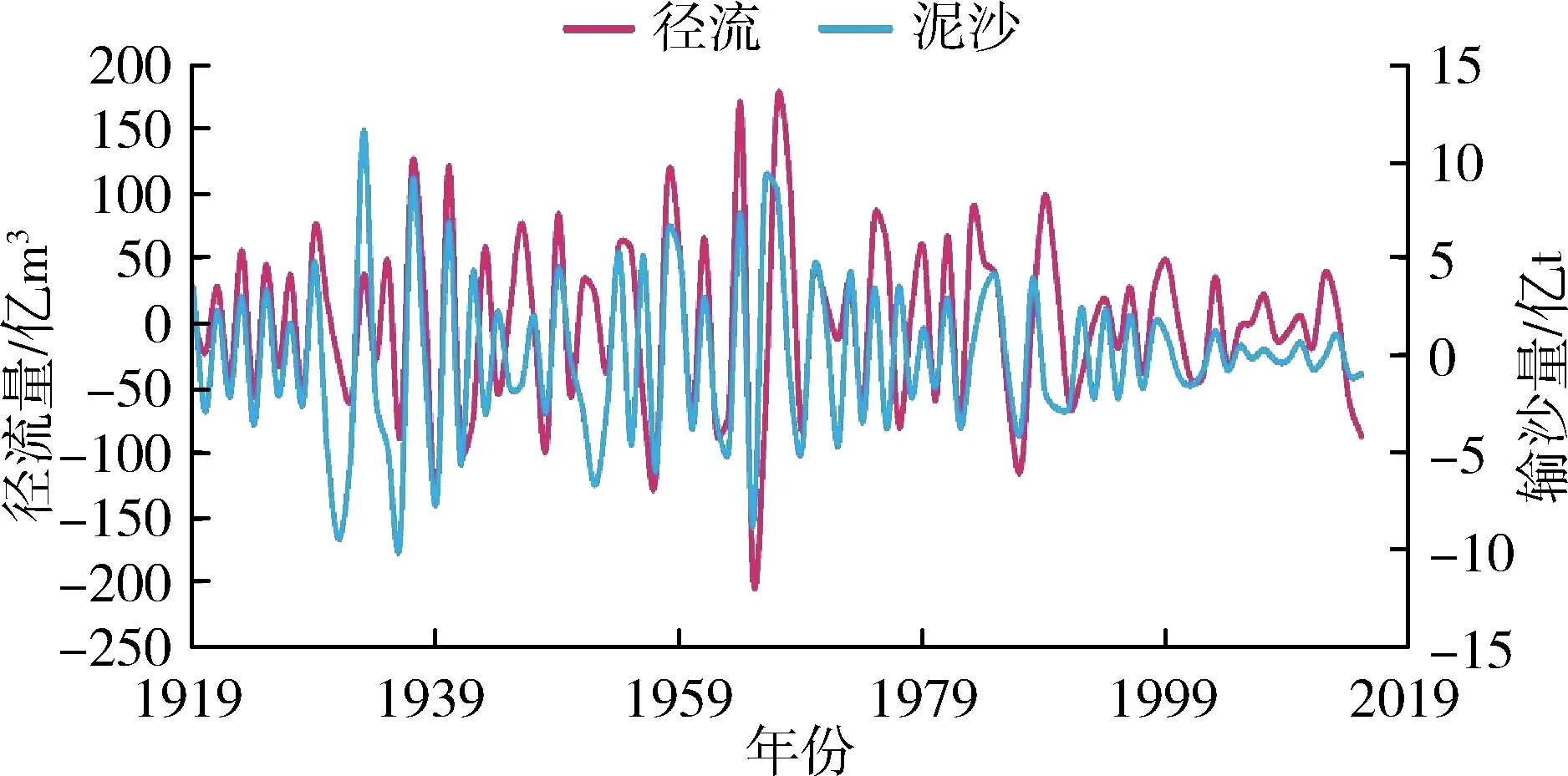
(a)IMF1分量
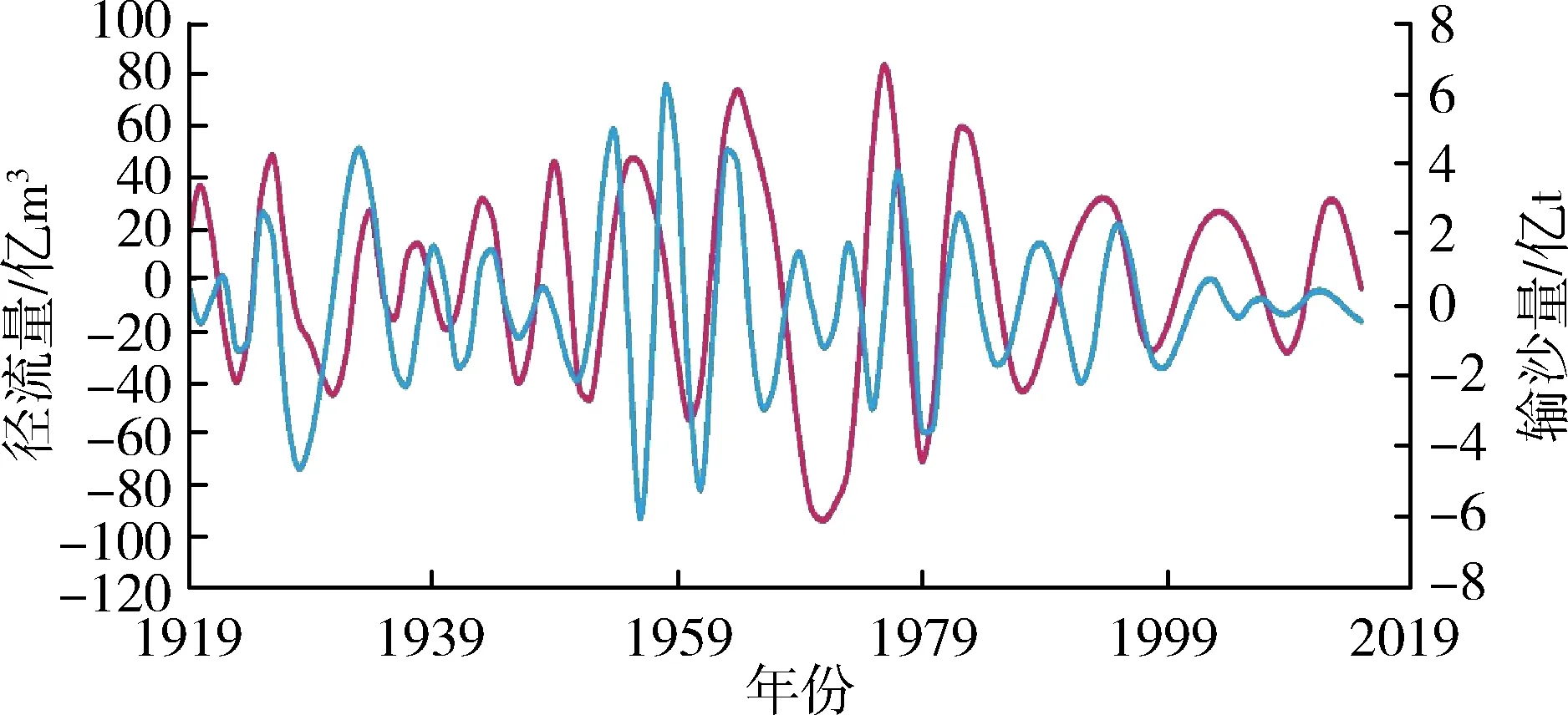
(b)IMF2分量
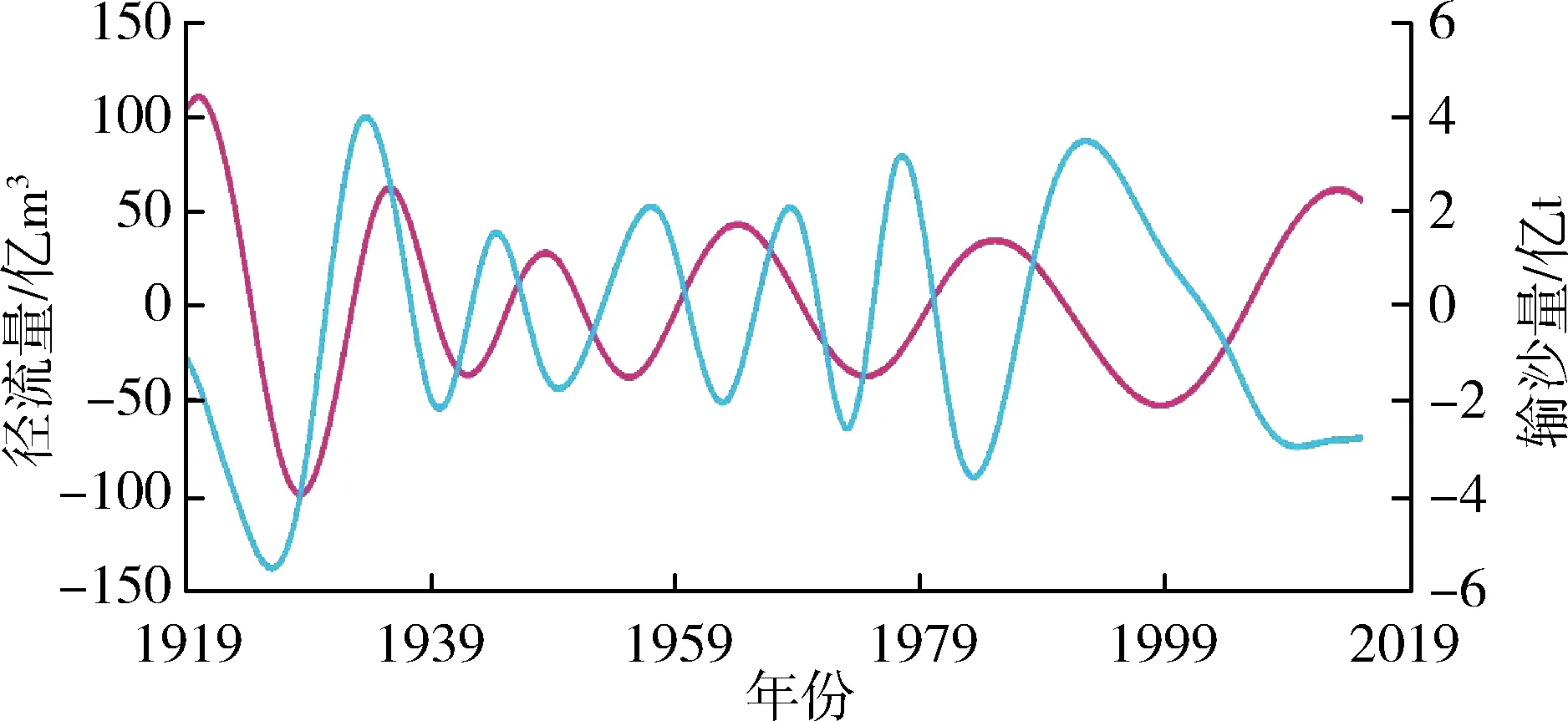
(c)IMF3分量
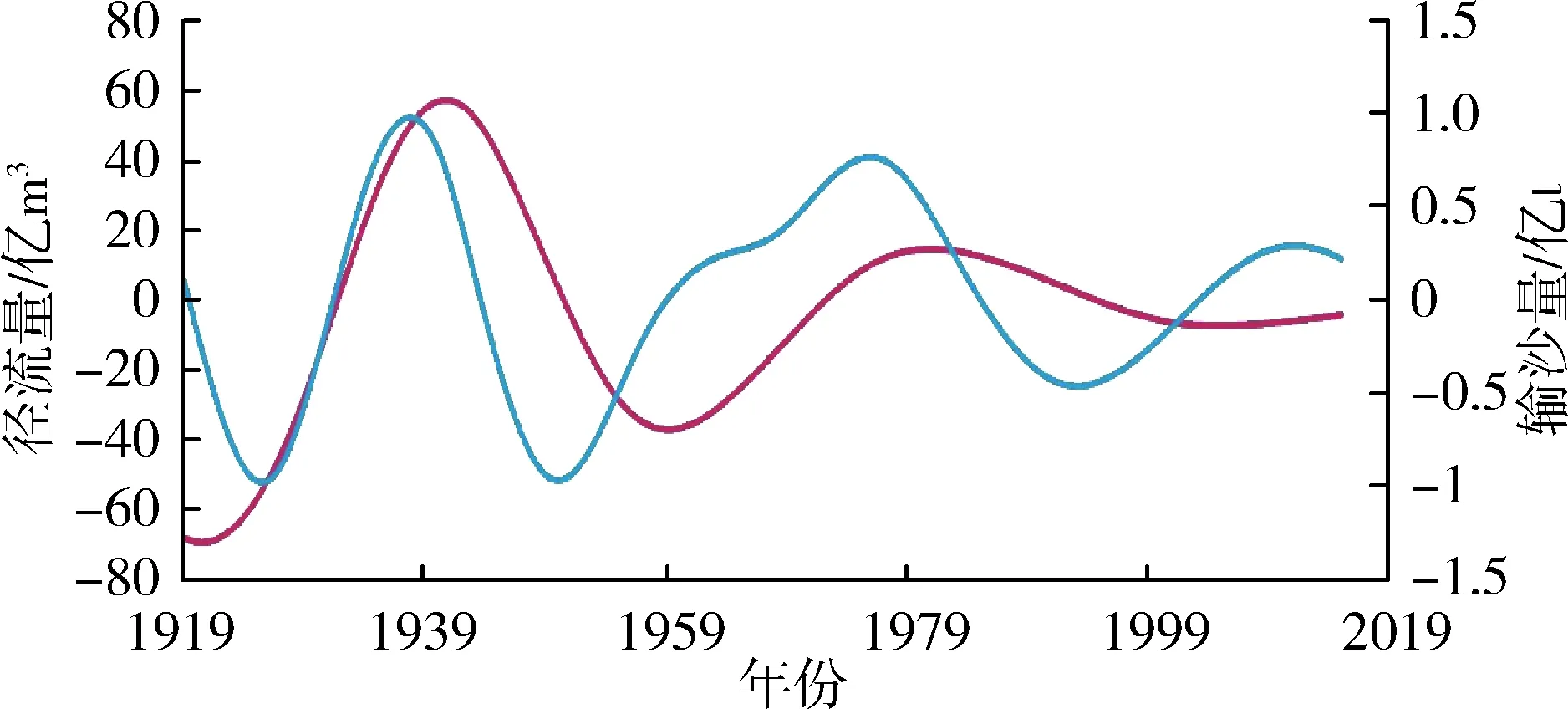
(d)IMF4分量

(e)RES分量
为16 a和15 a,IMF4分量的准周期约为35 a和28 a,可见径流和泥沙各IMF分量周期性关系在不同时间尺度上变化规律基本保持一致。这表明水沙相关性密切,水沙长时间序列在模糊特征下具有确定性特征,即存在波动周期的确定性,可为不同时期水沙联合预测、水沙变化特征研究提供参考。径流量、输沙量原始序列影响因素较多,经过EMD分解后随着分解层数的增多分解尺度的加大,径流、泥沙的干扰信息被去除,影响因素减少,有效信息增多,在不同的分层下表现为越来越有规律性。在趋势变化方面,表现为分解序列更有序,系统由无序到有序过渡的趋势性。特别是径流量、输沙量的趋势项呈现出较强的规律性,都呈现先上升后逐渐下降的趋势,径流上升速度比泥沙上升速度略快,二者趋势走向基本同步。
潼关水文站径流量、输沙量的趋势项在1950年左右分别出现拐点,在之后很长一段时间内不断减少,这是受自然和人类活动等多重因素影响的结果。1949年以来,水利工程建设、河道外取水、水土流失综合治理措施和修建淤地坝等生态工程建设的增加及其他人类活动干预对水文系统产生重大影响,使潼关水文站径流量,输沙量出现明显的减少[17]。整体而言,年径流量与年输沙量随时间表现为显著下降的趋势与文献[18]的结论相符。这表明原序列经EMD分解的RES分量可以反映径流量、输沙量整体的变化趋势,即低频模态分量控制着序列变化的全局和趋势。
2.2 信息熵分析
利用前文方法计算径流量、输沙量分解序列的信息熵结果见表1。径流量、输沙量IMF1分量对应的波动周期为短周期,IMF2分量对应的波动周期为中周期,IMF3分量对应的波动周期为中长周期,IMF4分量对应的波动周期为长周期,因RES分量缺乏周期波动,故不与IMF分量作对比。

表1 径流量与输沙量分量信息熵
由表1可见,径流量和输沙量原序列熵值较大,径流量熵值拐点首次出现在IMF1处,输沙量熵值拐点出现在IMF2处。表示随着分解层数的增多、分解尺度的加大,径流、泥沙分解序列表现为越来越有序,影响因素越来越少,系统呈现由不稳定向稳定过渡、由无序到有序的过渡的趋势性,因此信息熵值减小。但当分层过多,分解尺度过大,使系统的其他影响因素体现出来,从而使得信息熵值增大。
原序列对应的径流熵值比泥沙熵值稍大,可以判定径流系统较泥沙复杂,须密切关注径流量的变化。径流、泥沙各序列信息熵值变化基本同步,则表明径流量、输沙量之间关系应表现为同步变化或者异步变化特征,由径流量、输沙量原序列经EMD方法分析得知二者满足同步变化关系。
2.3 互信息分析
为了深层次分析潼关水文站径流-泥沙的关系,计算各序列与原序列之间的互信息熵值以及径流量与输沙量原序列之间的互信息熵值,结果见表2。

表2 径流量和输沙量原序列与其分解序列之间的互信息熵值
由表2可知,径流量、输沙量的原序列与RES分量之间的互信息最大,可见如果径流、泥沙系统比较复杂,为了便于研究径流、泥沙变化可采用RES分量数据信息阐述原始数据信息,并利用趋势项变化特征观察其整体发展态势。径流原序列与各IMF分量的互信息呈现递增的趋势性,即它们之间的共有信息量越来越多,原序列与IMF4的互信息最大,说明IMF4对径流原序列的贡献程度最大。对于径流IMF分量而言,低频分量与原序列的互信息较大,所以低频分量所携带的信息量比较多,因此对径流量宜采用长周期研究比较可靠。泥沙原序列与各IMF分量的互信息先减小后增大,泥沙原序列与IMF1互信息最大,说明IMF1对泥沙原序列的贡献率最大。对于泥沙IMF分量而言,高频分量与原序列的互信息较大,高频分量所携带的信息量比较多,因此对输沙量宜采用短周期研究比较可靠。
为了更进一步研究径流量、输沙量之间的关系,计算了径流与泥沙之间原序列及各分解序列的互信息熵值,原序列之间为0.689,IMF1分量之间为0.575,IMF2分量之间为0.338,IMF3分量之间为0.534,IMF4分量之间为0.675,RES分量之间为1.410。可以看出,趋势项之间的互信息最大,这是由于经EMD方法分解后排除了干扰,使径流、泥沙的有效信息充分体现出来,从而使两者之间的趋势项互信息比原序列之间的互信息大。原序列之间互信息也较大,表示虽然径流、泥沙原序列的影响因素比分解序列要复杂,系统比较无序,但是原序列信息量比较多。对于各分解序列来说,互信息基本呈现递增的趋势性,表示经EMD分解排除干扰后各系列之间的关联性增大,它们之间的共有信息量逐渐增大。对于径流量与输沙量经EMD分解的各IMF分量而言,径流量与输沙量对应的长周期IMF4分量互信息最大,因此径流量与输沙量关系及其变化特征宜采用长周期的研究。
3 结 论
潼关水文站年径流量与年输沙量随时间表现为显著下降的趋势,且径流量和输沙量有着很强的相关性,这种相关性不仅体现在宏观趋势上,而且还体现在微观局部特征上,具体表现为在多时间尺度下波动特征基本同步。EMD方法与信息熵结合分析表明,径流量与其长周期分量互信息最大,因此对径流量变化特征宜采用长周期研究比较可靠;输沙量与其短周期分量互信息最大,因此对输沙量变化特征宜采用短周期研究比较可靠;而径流量与输沙量的长周期分量及趋势项互信息较大,所以黄河中游潼关附近水沙关系可采用长周期研究,趋势项分量数据信息阐述原始数据信息比较可靠。

