CPU?GPU平台上的高速MPSK并行解调算法
吴涛 闫迪 刘燕都 赵江

摘 要: 针对多进制数字相位调制信号特点,采用数据并行方法,将连续信号流分解为多个信号块以实现并行处理。研究一种基于三维迭代搜索的载波相位?码元相位联合估计算法,在本地构造载波信号的搜索库,利用分段码元相关法从搜索库中挑选出与待处理信号相似度最高的载波信号作为同步载波。通过迭代搜索方法逐步缩小搜索库,降低计算量。仿真结果表明,与克拉美?罗下限相比,解调损失小于0.1 dB。在惠普工作站与英伟达K20平台上搭建验证系统,系统的处理速率可达625.9 MB/s。
关键词: CPU?GPU平台; 高速MPSK; 并行解调; 相位模糊; 三维迭代搜索; 数据并行
中图分类号: TN911.72?34;V443+.1 文献标识码: A 文章编号: 1004?373X(2019)13?0009?06
A parallel demodulation algorithm based on CPU?GPU platform
for high?rate MPSK signal
WU Tao1, YAN Di1, 2, LIU Yandu1, ZHAO Jiang3
(1. Department of Electronic and Optical Engineering, Space Engineering University, Beijing 101416, China;
2. The Unit 61646 of PLA, Beijing 100192, China; 3. China Satellite Maritime Tracking and Control Department, Jiangyin 214431, China)
Abstract: According the characteristics of multiple phase shift keying (MPSK) signal, the data parallel method is used to decompose the continuous signal stream into multiple signal blocks to realize parallel processing. A carrier phase?code element phase joint estimation algorithm based on three?dimensional iterative search is studied. The search library of carrier signal is constructed locally, and then the carrier signal with the highest similarity with the signal under processing is chosen from the search library by means of segmentation code element correlation method to act as the synchronization carrier. The iterative search method is used to gradually deflate the search library to reduce the computational quantity. The simulation results show that, in comparison with the Cramer?Rao lower bound, the demodulation loss of the proposed algorithm is less than 0.1 dB. The verification system was built on HP workstation and NVIDIA K20 GPU, which realized the processing rate of 625.9 MB/s.
Keywords: CPU?GPU platform; high?rate MPSK; parallel demodulation; phase ambiguity; three?dimensional iterative search; data parallelism
0 引 言
卫星通信数传正朝着更高码率、更大带宽的方向发展,而高速数传解调是一个重要问题。CPU?GPU平台计算能力飞速发展,在其上进行数字信号处理已成为一种发展趋势[1?3]。本文针对CPU?GPU异构平台上的高速MPSK信号解调算法进行研究。
目前文献公开的三种高速并行解调架构分别是IEC(Interstate Electronics Corporation)[4],PRX(Parallel Receiver)[5]和APRX(All?digital Parallel Receiver)[6]。其中,APRX实现简单,资源消耗少,被广泛使用。国内在APRX基础上进行了一些数传解调器的研究[7?8]。尽管如此,APRX仍有两点不足:一是APRX要求采样率必须为数据率整数倍,为避免采样混叠,信号中心频率需随数据率选取[9?10];二是基于APRX的并行解调器不适合在CPU?GPU平台上运行,基于APRX的各种解调算法均存在反馈调整,用来纠正载波频差和定时误差等,在CPU,GPU中实现这种反馈需要频繁的线程同步,带来较大的同步开销,且反馈操作增加了算法内部的数据依赖,降低了算法的并行性。因此,APRX并不适合于CPU?GPU平台。
考虑到CPU?GPU平台的特殊性,本文采用数据并行思想,将高速信号流分解为多个信号块,通过同时处理多个信号块实现并行解调。这要求信号块的处理必须是独立的、互不相关的。一般而言,信号的相干解调使用反馈环路方法,如果用于本文的信号块处理,必然不能满足要求。当信号块长度足够短时,可以认为在这段时间内信号的载波参数是恒定不变的,因此,本文将信号块的相干解调问题转化为载波参数估计问题,各信号块的载波参数估计可以独立进行。首先提出一种基于三维迭代搜索的载波相位?码元相位联合估计算法,迭代搜索空间是<载波频率,载波初相,码元相位>。通过不断缩小搜索空间的每个维度的范围,大幅减小搜索计算量,因此称之为迭代搜索。然后研究了算法在CPU?GPU平台上的具体实现方法。最后在惠普Z820+NVIDIA TESLA K20 硬件平台上搭建验证系统。
1 并行解调算法
1.1 算法原理
算法利用互相关的原理,在本地构造出大量搜索信号,将搜索信号逐一与接收信号做相关,当相关值最大时,就得到了接收信号的参数估值。由于有3个待估参数,所以搜索空间是三维的,用[
互相关是反映两个信号相似程度的常用方法,两个信号越接近,相关值越大。以QPSK信号为例,可表示为:
码元[a]是随机分布的,故[J]为0。可见,由于调制信息影响,即使[f=fc+fd],[φc=φ],[J]依然为0。若按式(5)的方法进行相关,[J]就能反映接收信号和本地搜索信号的相似程度。通过寻找最大互相关值,就能获得载波频率和载波初相的估计值。本文称之为分段码元相关法。
1.2 算法流程
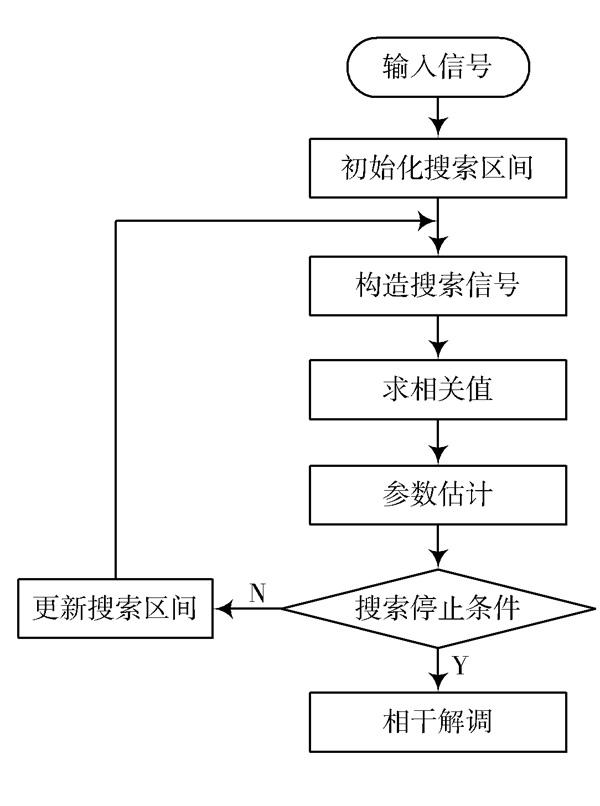
算法流程如图1所示,基本步骤如下:
步骤1:初始化搜索空间。搜索空间初始值[图1 算法流程图

步骤3:求相关值。利用分段码元相关法,求接收信号与搜索信号的相关值[CORRi,j,l],对于每一种搜索信号有[N3]个不同的码元初相,故有[N3]个相关值。
1) 本次迭代的相关值小于上次迭代;
2) 载波频率的步长小于50 Hz;
3) 载波初相的步长小于0.01。
搜索空间的更新方法是:从[
1.3 分段码元相关法
分段码元相关法在计算互相关值时,消除调制信息影响。其原理是在每个码元周期内做相关,得到一系列相关值,将这些相关值的绝对值求和得到总相关值,共分为两个步骤:
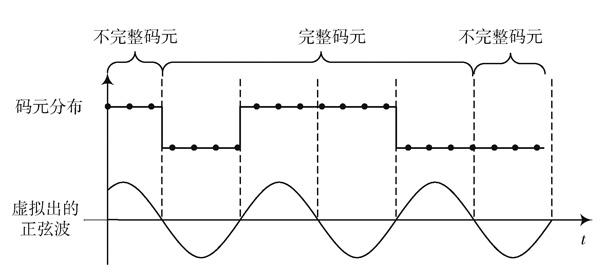
步骤1:确定码元分布情况。
码元分布由码元初相和码元周期决定,[φb]分布在[0,2π]内,码元周期由实际码速率[Rs]决定,[Rs]由码多普勒[Rsd]和标准码速率[Rs0]组成:
若虚拟出一个频率为[Rs2],初相为[φb2]的正弦波,那么正弦波的过零点就是码元变化时刻,介于两个相邻过零点之间的采样点是一个码元周期,如图2所示。
图2 码元分布情况确定方法

步骤2:计算积分。
接收信号和本地搜索信号的混频信号为[mix(k)]。假设码元分布情况如下:第一个不完整码元的采样点数量是[x],完整码元的个数是[y],每个完整码元内的采样点数是[N(i),i∈[1,y]],最后一个不完整码元的采样点数量是[z]。那么,积分值[CORR]如下:
1.4 相位模糊匹配方法
用锁相环方法对QPSK信号进行解调时,由于本地恢复载波与QPSK载波相位存在多种可能的相位差,从而导致解调结果存在模糊[11],本文同样存在这种模糊现象。假设本地载波与QPSK载波同频,只存在相位差[Δφ],正交下变频后[I],[Q]路如式(9)所示:
表1 不同[Δφ]下QPSK解调的相位模糊

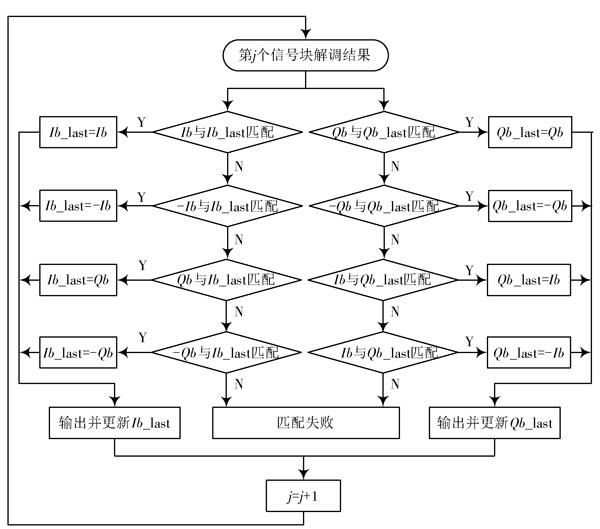
每个信号块独立解调,其[Δφ]不一致,导致相位模糊也不一致,需要对不同信号块的相位模糊进行匹配。本文提出一种基于数据冗余的相位模糊匹配方法,基本原理是利用相邻信号块的重叠,调整后一个信号块的模糊使之与前一个模块一致,最终使得所有信号块的模糊都一致。如图3所示为信号块冗余分割方法,[L]为信号块长度,[L0]为信号块重叠区长度。
图3 信号块冗余分割方法
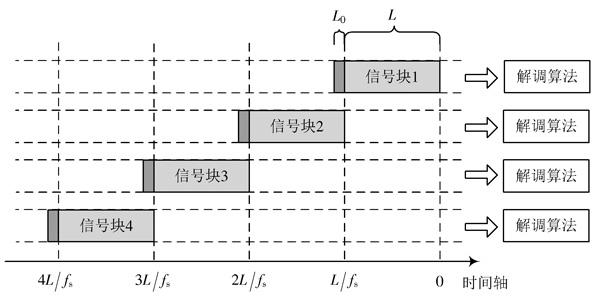
图4 相位模糊匹配方法流程图
2 仿真与测试
为了验证算法解调性能和实际执行效率,本文进行Matlab仿真,并在CPU?GPU平台上对算法进行测试。统一使用以下调制参数:调制方式为QPSK,符号率[Rs=] 1 Gb/s,载频频率[fc=1] GHz,采样频率[fs=4] GHz,多普勒频率[fd=]12 345 Hz,载波初相[φc=0.45] rad,码元初相[φb=0.5] rad。
2.1 迭代搜索过程的仿真
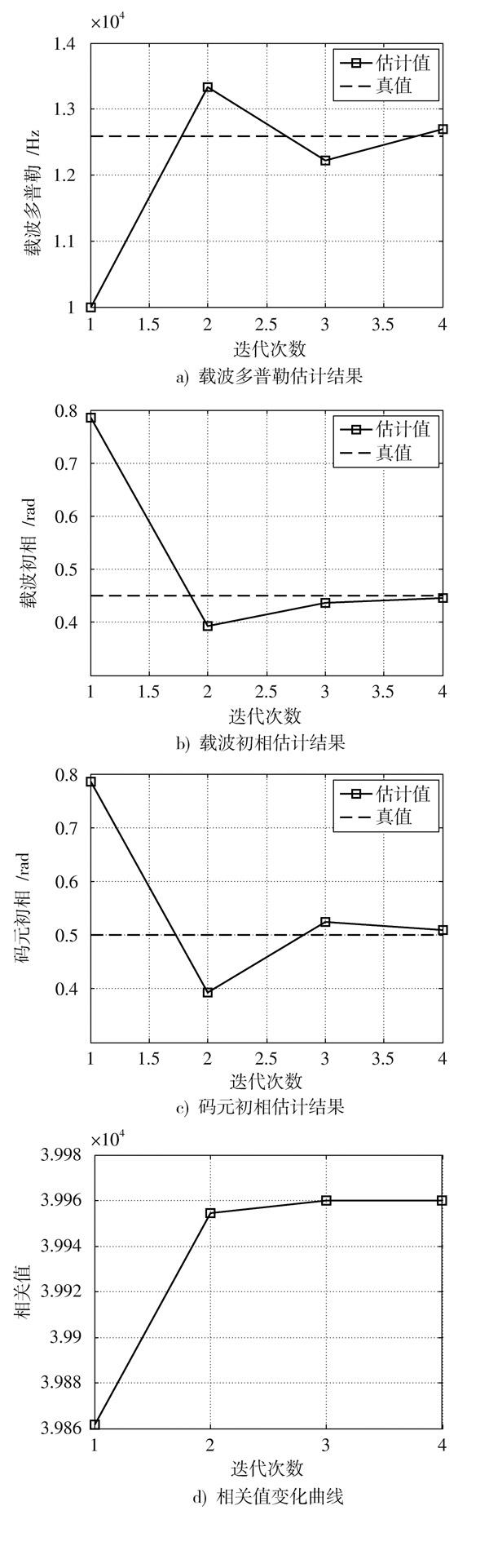
设置信噪比[EbN0=]10 dB,载波多普勒的初始搜索空间是(-20 000,-10 000,0,10 000,20 000),载波相位的初始搜索空间是[π8,π4,3π8,π2],码元相位的初始搜索空间是[π4,3π4,5π4,7π4]。仿真结果如图5所示,图5a)是载波多普勒估计结果,图5b)是载波初相估计结果,图5c)是码元初相估计结果,图5d)是相关值变化。可见,参数估值随着迭代过程逐渐逼近真值,相关值增加到一定程度后变化很小。
大量仿真表明,经过4次迭代后能完成参数估计,共进行80+64+64+64=272次相关运算。如果直接进行三维搜索,为了达到与迭代搜索同样的估计精度,搜索空间步长需要设置为当前的[127],需进行(5×27)×(4×27)×(4×27)=1 574 640次相关运算。可见,迭代搜索方法将相关运算次数减少为0.017%,大大减少了计算量。
图5 仿真结果
2.2 算法解调性能仿真
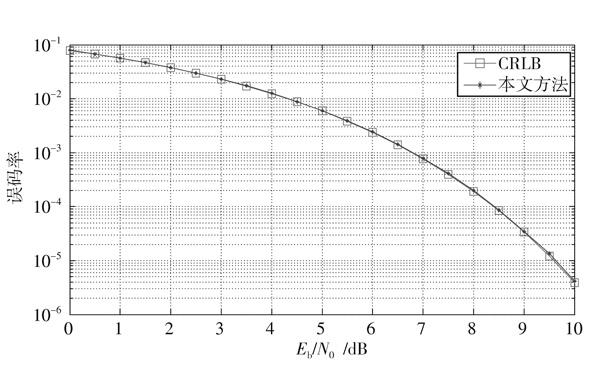
为了验证算法的解调误码性能,对[EbN0]在[0,10] dB区间内的信号进行解调,统计误码率结果与克拉美?罗下界(Cramer?Rao Lower Bound,CRLB)如图6所示。从仿真结果可以看到,在[0,10] dB区间内,解调损失在0.1 dB以内。
2.3 CPU?GPU平台上的测试
为进一步验证算法的执行效率,在CPU?GPU平台上搭建验证系统,系统硬件配置如表2所示。
图6 误码率仿真结果比较
验证系统由信号调制机和信号解调机两部分组成,二者通过万兆网连接,信号调制机产生8 bit量化的QPSK信号后,传给信号解调机进行处理。信号调制机采用“多线程计算,轮流输出”的方法,每个线程产生时间上间隔的QPSK信号块,按顺序轮流读取各线程产生的信号块,就得到了时间上连续的QPSK信号流。
信号解调机采用如图7所示的框架,在CPU中完成信号流分割,将信号块填充到信号池。进程管理器创建多个解调进程,将信号块传入GPU进行处理。结果综合使用相位模糊匹配方法,将不同信号块的解调结果再加工合并为最终解调结果。
表2 系统硬件配置参数

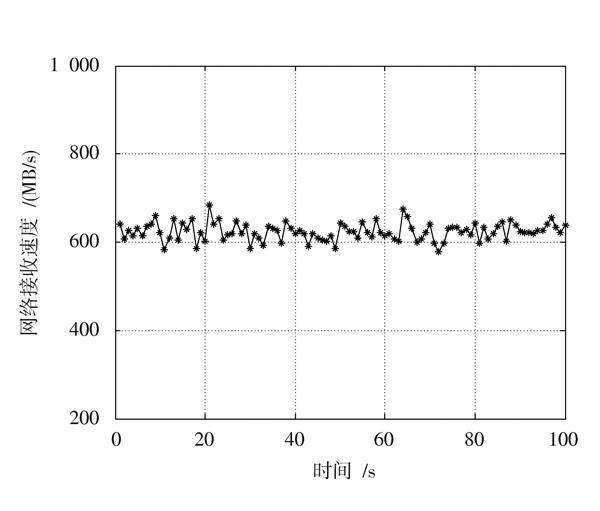
如圖8所示为运行状态的系统,100 s内信号解调机的网络接收速度如图9所示,平均处理速率是625.9 MB/s,换算为码速率后是313.0 Mb/s。
图8 系统硬件组成

图9 信号解调机的网络接收速度
3 结 论
本文提出一种CPU?GPU平台上的高速MPSK解调算法,给出了算法的具体步骤,并在惠普Z820工作站上进行了编程实现。仿真结果表明,[0,10] dB区间内的解调损失在0.1 dB以内,验证系统实现了313.0 Mb/s的QPSK实时解调。313.0 Mb/s解调速度是在一块NVIDIA TESLA K20上实现的,与FPGA平台相比并没有明显优势。但本文方法的最大优势是其具有可扩展性,通过扩展GPU计算资源就能方便地增加解调进程数目,进而提高系统解调速率。
参考文献
[1] 牛炯,申晋晋,陈倩.高频地波雷达实时信号并行处理方案及实现[J].中国海洋大学学报,2017,47(2):56?61.
NIU Jiong, SHEN Jinjin, CHEN Qian. Real?time signal parallel processing scheme and realization of HF ground wave radar based on CPU+GPU architecture [J]. Periodical of Ocean University of China, 2017, 47(2): 56?61.
[2] 王子潇.基于CUDA GPU平台的脉冲多普勒雷达信号模拟软件[D].北京:北京理工大学,2016:1?3.
WANG Zixiao. A PD radar simulation software based on CUDA GPU platform [D]. Beijing: Beijing Institute of Technology, 2016: 1?3.
[3] 武新波.基于CUDA的GPS软件接收机研究[D].北京:北京理工大学,2015:3?4.
WU Xinbo. Research on GPS software receiver based on CUDA [D]. Beijing: Beijing Institute of Technology, 2015: 3?4.
[4] 林长星.2 Gb/s高速通信解调技术及其实现研究[D].北京:清华大学,2012:31?33.
LIN Changxing. Research on demodulation technique and its implementation for 2 Gb/s high speed communication [D]. Beijing: Tsinghua University, 2012: 31?33.
[5] SRINIVASAN M, CHEN C C, GREBOWSKY G, et al. An all?digital high data?rate parallel receiver [J]. Surface science, 1997, 604(15/16): 1294?1299.
[6] SADR R, CAIDYANATHAN P, RAPHAELI D, et al. Parallel digital modem using multirate digital filter banks [M]. California: JPL Publication, 1994: 1?112.
[7] 梁侠,任海根,徐先超,等.800 Mb/s高速解调器的定时恢复算法及实现研究[J].现代电子技术,2007,30(23):1?3.
LIANG Xia, REN Haigen, X? Xianchao, et al. 800 Mb/s timing recovery algorithm and implementation for high speed demodulator [J]. Modern electronics technique, 2007, 30(23): 1?3.
[8] 郭晓峰,郑雪峰,卢满宏,等.高速数传QAM解调器设计及应用[J].遥测遥控,2011,32(3):21?25.
GUO Xiaofeng, ZHENG Xuefeng, LU Manhong, et al. Design and application of high?data?rate QAM demodulator [J]. Journal of telemetry, tracking and command, 2011, 32(3): 21?25.
[9] 唐婷,杜瑜.全数字化高速数传解调器的设计与实现[J].科学技术与工程,2016,16(14):32?35.
TANG Ting, DU Yu. The design and realization of fully?digitalized high?rate data demodulator [J]. Science technology and engineering, 2016, 16(14): 32?35.
[10] 曾辉.基于全数字高速并行接收结构APRX的解调技术研究[D].成都:电子科技大学,2013:3?5.
ZENG Hui. Research on demodulation techniques based on a parallel all?digital receiving structure named as APRX [D]. Chengdu: University of Electronic Science and Technology of China, 2013: 3?5.
[11] 保骏.QPSK、SQPSK信号解调相位模糊及其对Viterbi译码的影响[J].兵器装备工程学报,2011,32(3):53?55.
BAO Jun. Demodulation phase ambiguity of QPSK and SQPSK and its influence on Viterbi decoding [J]. Journal of ordnance equipment engineering, 2011, 32(3): 53?55.

