基于最大上座率春运火车票票额分配模型
杨洁
[提要] 春运是牵动民生的重要问题。本文在分析造成春运难的主要原因及已有的解决方案后,考虑优化票额分配,以最大效率的利用已有列车资源。以最大上座率为目标,通过理论分析,从预测和决策两部分实现合理票额分配。根据往年预售期旅客购票趋势统计数据,利用特征识别法将预售期分为不同的阶段;预测阶段,在以往预售期内购票需求已知的条件下,利用基于残差修正的灰色模型对本年预售期内不同时段的购票需求进行合理预测;决策阶段,以最低上座率保障值为约束条件,考虑长途因子,以半马尔可夫决策过程为基础,建立单次决策上座率最大模型,并以此推广到整个预售期,建立以最大上座率为目标的列车票额分配模型。
关键词:票额分配;特征识别;灰色模型;半马尔可夫过程;最大上座率
基金项目:中国矿业大学2018年度大学生实践创新训练计划项目(项目编号:201810290125X)
中图分类号:U293.22 文献标识码:A
收录日期:2019年4月16日
“春运回家难”是铁路客运中存在已久的热点问题,具有鲜明的区域性与时间性,近年来得到了较为广泛的关注与研究。任雪凌通过对官方春运统计大数据进行分析,认为春运购票难的主要原因有:需求强盛而供给不足,定价策略不确定,存在恶意购票的行为。目前针对解决“春运一票难求”提供的方法也主要针对以上三个方面,如增加铁路运力与改革铁路运营体制;依据旅客对票价敏感程度不同,实行动态票价;落实相关法律制度,对“网络黄牛”进行规范、整治;也有一些从优化车站和网上购票进行研究,如基于排队论的售票窗口动态优化;设立网络购票服务点,协调网络售票与窗口售票预售期。然而,供给动力不足属于外在硬性因素,涉及国家重大项目规划,无法轻易进行调整;定价策略需要考虑人们心理价位的承受范围,铁路为国民经济带来的利润等多方面的问题,并且国家在2006年以前曾制定过票价调节机制,但并没有取得满意的结果。
本文考虑在不改变铁路部门现有结构和增加动力的基础上,优化列车在各停靠站的票额分配计划,充分利用列车资源,来实现缓解春运压力。目前,票额发售仍然采用“先到先得”的方式,这样会出现因短途旅客提前购票,长途旅客购票需求无法满足,出现“车上空座,车站没票”的情况,降低了列车资源利用率。强丽霞、贺振欢通过对不同范围内控制OD的优先级排序,实现能力分配的引导,然后用Logit模型进行建模,得到客流分配方案;强丽霞以客运周转量和平均运距最大化为目标构建了双目标优化模型,实现票额预分优化;赵烨根据不同OD行程的购票特征构造购票强度函数,假设旅客总是基于当前剩余能力选择最小费用方案出行,在列车定员的严格约束下,求解客流分配方案;龚辉锋以总服务率为目标,在合理约束下,建立单向火车票动态优化模型;包云等针对高速铁路提出“嵌套式”票额分配模型来保护长途OD的需求。以上研究主要将票额进行提前预分,未充分考虑预售期不同OD购票需求的实时变化情况,不利于铁路运输能力的充分挖掘与效益的提高。
本文将春运主力军抽象为长途旅客,从铁路客运管理层面出发,聚焦于铁路客运售票组织,在供给不变的情况下,研究单列车在沿途停靠站的票额分配计划,制定列车票额销售控制策略。根据往年预售期旅客购票趋势统计数据,利用特征识别法将预售期分为不同的阶段;在前五年预售期内购票需求已知的条件下,利用基于残差修正的灰色模型预测本年预售期内不同时段的购票需求;以最低上座率保障值为约束条件,考虑长途因子,以半马尔可夫决策过程为基础,建立单次决策上座率最大模型,并以此推广到整个预售期,建立以最大上座率为目标的列车票额分配模型。
一、决策问题描述
若每次状态的转移只和上一个时间点的状态有关而与之前其他时刻无关,则这样的状态转移过程称为马尔科夫过程。火车票售票过程可以认为是一个离散时间的随机过程,且每次售票都没有后效性的马尔科夫决策过程。本文中,我们以每次售票请求作为事件的触发器,以尽可能大的全局上座率为目标函数,在每次决策后,進行状态转移与更新,这样就得到了一条决策链,保证了在划分的时间段内都能达到高上座率,一定程度上避免了春运时人流拥挤而部分车票未售出的情况。
二、预测与决策模型
(一)参数说明。首先定义文中出现的参数、变量与假设。
(二)基于特征识别和GM(1,1)的预测过程
1、特征识别法。根据以往购票统计数据可以得到预售期内的日购票强度分布,通过相关数据观测,发现在预售期的不同时段,购票需求强度具有显著差异。所以,考虑对预售期进行分段,这里选择按预售期内购票需求数据分布特征来识别,具体做法如下:
2、购票需求预测。如果能利用往年的数据对当年预售期内任意时段购票需求进行合理预测,则可以使得接下来的决策工作更有效地进行,决策结果更满足需要。如果将火车站作为一个系统,因为只知道往年客流量和购票需求等部分信息,则该系统是本征性的灰色系统。基于系统的这种性质,我们可以利用灰色预测理论对列车在预售期的第T个阶段的购票需求CT,进行有效预测。一些研究表明,该理论对解决灰色系统的趋势预测问题有独特的优势。
将数据代入传统的灰色预测模型进行求解,计算后发现,残差检验结果并不理想,于是考虑对传统模型进行优化,建立基于残差修正的灰色预测模型。
因为车站系统为本征性灰色系统,较多未知因素随着时间的推移会对系统带来影响,所以该模型对于长期预测是存在问题的,没有太大意义。基于这种情况,可以选择预售期内每一天的前五年购票需求数据,利用残差修正模型求解得到该天数据预测值。则在预售期T阶段,购票需求预测值为:CT=xi。
三、决策理论分析
预售期对购票需求决策流程如图1所示。(图1)
图1 决策流程图

图2 状态层
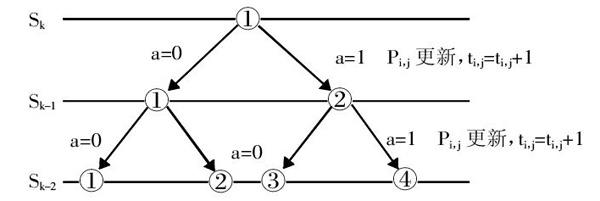
对状态层k上购票需求pi,j决策结束后,需要计算在a=0或a=1两种情况下带来的上座率收益bk。该收益由两部分组成:购票上座率收益b1k和额外上座率收益b2k。购票上座率收益是指pi,j需求带来的上座率,额外上座率是指(i,j)区间裂解后的带来的上座率。例如,只有五个车站,当购票需求p1,3到达时:决策a=1时,剩余座位可被裂解为(3,4)、(3,5)、(4,5),并且在以后可以以一定的概率被售出,这种情况下带来的上座率收益就是(1,3)和裂解以后区间上座率的和;决策a=0时,剩余座位可被裂解为(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)、(4,5),这种情况下带来的上座率收益就是裂解以后区间上座率的加权和。
四、总结
本文主要针对春运期间火车购票难的问题,并且基于已有的一些模型及方法,给出一套合理的售票决策方案以求达到最大的上座率,力求使尽可能多的人买到票。本文在介绍模型时,主要分以下几部分:(一)预售期的划分,根据不同时间段的购票强度不同并结合相应的概率知识,对预售期进行划分;(二)购票需求预测,结合往年购票数据,对当年的购票情况进行合理预测,可使后续模型更贴近实际,迎合往年购票情况的发展趋势;(三)在各预期目标及限制条件下,给出较为合理的售票决策模型。基于以上三部分,给出了一套系统的基于最大上座率的售票决策算法,以期待在实际应用中能有较好的成效。
主要参考文献:
[1]任雪凌.从供需角度分析春运火车票购票难[J].中国集体经济,2018(3).
[2]吴尤可.从春运火车票不涨价说起——春运难题解决方案探析[J].价格理论与实践,2007(3).
[3]张向辉.大数据背景下铁路客运组织策略研究[J].甘肃科技,2017.33(2).
[4]陈磊.基于排隊论的火车站售票排队系统的分析与研究[J].成都信息工程学报,2010.25(6).
[5]郭培奇,张健.“互联网+”背景下进城务工人员购票问题探析[J].城乡建设与发展,2016.
[6]强丽霞,贺振欢.基于客流分配技术的铁路旅客列车票额分配方法研究[J].铁道运输与经济,2017(9).
[7]强丽霞.旅客列车票额智能预分方法研究[J].铁道学报,2018.40(9).
[8]赵烨.考虑售票策略的高速铁路客流分配方法[J].铁道学报,2018.40(9).
[9]龚辉锋.单向火车票动态分配优化模型与软件实现[J].沈阳大学学报,2009.21(6).
[10]包云,刘军,马敏书,等.高速铁路嵌套式票额分配方法研究[J].铁道学报,2014.36(8).
[11]刘晓琴,姚晓晖,庞雷.马尔科夫链模型在铁路春运客流预测中的应用[J].安全科学技术,2010(12).
[12]刘帆洨,彭其渊,等.铁路客运票额预售控制决策模型研究[J].铁道学报,2018.40(1).

