分辨学生自然结构的正误

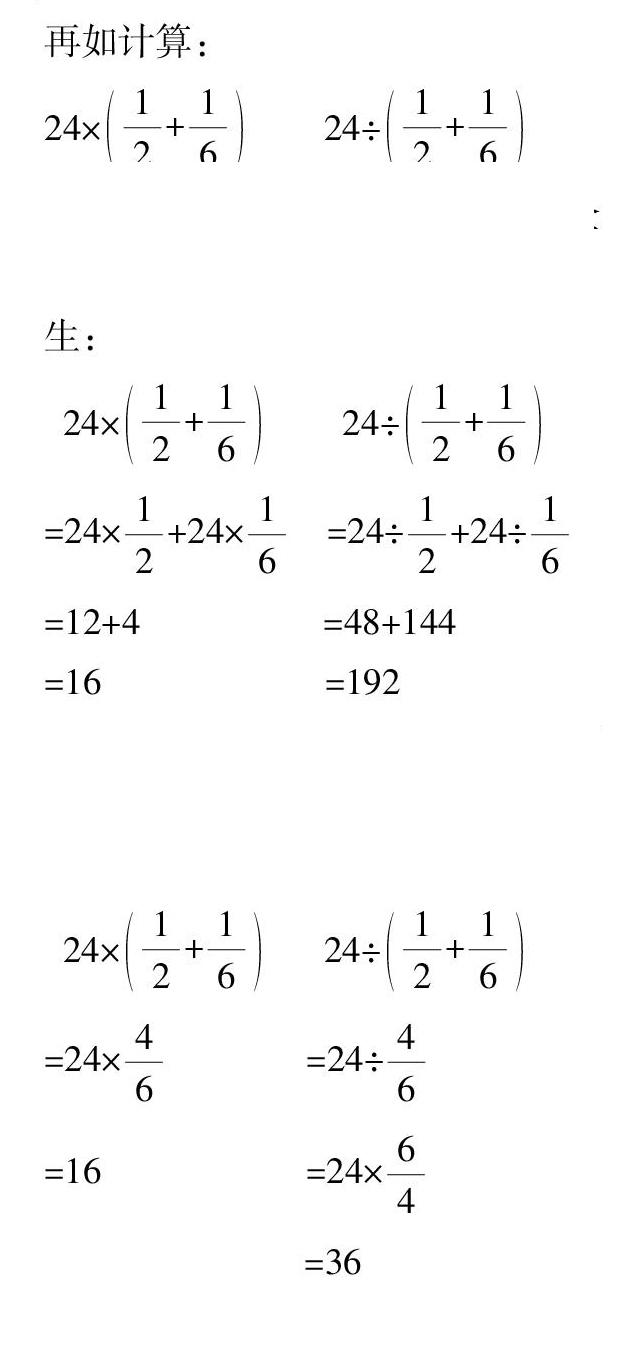
摘  要：学生在刚开始进入小学的时候，做题经常会发生“想加却减，想减又加”的情况，这时，教师不应很轻易地就判断学生是错误的，而是要分析这种问题出现的原因，再通过这些原因来具体分析，以此加强学生对加减运算的理解，从而减少这种问题的发生。

关键词：自然结构;加工结构;人为习惯

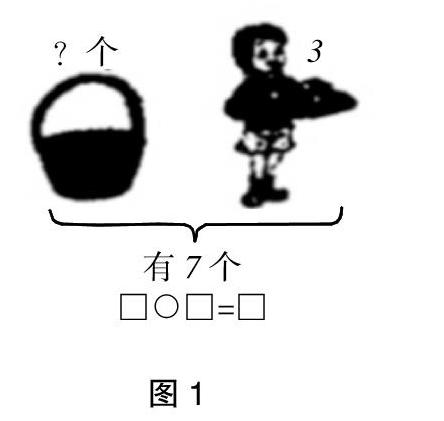
初入小学的学生在答题时经常会发生“想加却减，想减又加”的情况。就如同下面这道问题：

此题是：已知苹果的总数量是7个，小朋友拿走了3个，那么篮子中还剩下多少个苹果呢？这就是简单的减法运算：7-3=4，但学生经常会这样列式：4+3=7。还有类似的题目：一群麻雀在电线杆上，飞走了3只，还剩下5只，那么原来共有多少只麻雀呢？此题就是简单的加法运算：3+5=8，但有的学生会这样列式：8-3=5。很明显这两道题都有一个相同点，那就是学生都知道问题的答案是什么。

那到底为什么会引起这种情况的发生呢？像这种情况，教师是该算学生对还是算学生错呢？

一、思维的自然与加工结构

学生的思维认知大概可分为这三个部分：①眼鼻耳等器官获得信息;②大脑中对信息的加工;③表达加工的信息。学生在表达上出现问题了，那么也就意味着获得知识的过程与加工信息的过程可能至少有一个出现了问题。

学生在解答上述两个问题时都有这样一个共同点，都是按照题中的所给出的信息顺序来写算式。比如第一个问题，题中的信息顺序为：空篮子、3个、7个，这三者之间能够很自然而然地得到：4+3=7，学生得到了这个算式就会很容易直接写出这个答案不再多加考虑，毕竟这个算式中已经包含了正确答案。

我们的阅读习惯大多都是自左往右、自上往下，所以我们获得的信息都是有先后顺序的，这个先后顺序会很自然地让我们得到一个思维结构。对于刚步入小学的学生而言，要对他们所获取的这些信息进行加工还是比较复杂的，因为他们的加工能力还是比较弱的，所以他们就会很容易按照得到这个自然思维结构来进行表达。这样也就可以比较容易解释学生为什么会列出上述算式。若我们将“4+3=7”“8-3=5”这两个算式的思维方式称为“自然结构”，“7-3=4”“5+3=8”这两个算式的思维方式称为“加工结构”，那么学生出现错误的重要原因就是这两个结构的顺序是不一样的。

学生之所以会形成这样一种自然的思维结构，这与他们的经历是密不可分的。就好比114×21标准的竖式计算应该为：

这种标准的竖式计算就是把“21个114相加”变成“1个114和20个114相加”。还有的学生会有别的方法来列出竖式，比如下面这种：

这种算式虽然不同于标准的算法，但与标准算法的中心思想还是如出一辙的，不同的只是他们的结构顺序不一样而已。

综上所述，学生在学习这类数学问题中的重难点就是获得知识的自然结构与对知识进行的加工结构这两者之间的差异性。这就要求老师要将教学重点放在转化自然结构和加工结构上并要对这两种结构进行充分了解。在学习中，不能盲目否定学生依据自然结构得出的结果，这样不但会约束学生的思维发散，而且还会削减他们在学习数学上的兴趣。所以对待这种由自然结构得出的结果的正确与否我们还需要进一步进行判断。

二、合理分析错误

对于上述由自然结构得出的结果，认为正确的是觉得学生已经理解了题中的数量关系，并且计算结果也是正确的;认为错误的是觉得学生还没有正确理解题目中的已知量和未知量，结果应写在等式的右侧。虽然题中的已知量和未知量不相同，但是还是应该将这两者结合起来思考。就像在方程的学习中我们把未知数当成已知数来用，并且用字母将这些未知数表示在算式中。我们可以将方程上的知识运用到前面这两个问题中，即可得到X+3=7和X-3=5。从这两个算式中我们就可以看出方程就是自然结构得出来的结果。

认为应将结果写于等式右侧其实是误解了等式。相等關系是等价关系中的一种，而等价关系应该是包含了以下这三个条件的：①自身性：A=A;②交换性：若A=B，即B=A;③传递性：若A=B，B=C，则A=C。其中的交换性就说明了等号前后的顺序是可以进行交换的，那么一定要将结果写在等式右侧的这一说法就是不正确的。这最多只能算作是大家约定俗成的习惯，从这方面来讲，通过自然结构得出的结果是应该被认可的。

三、识别自然结构的依据

当学生遇到自然结构与加工结构得出的结果不相同时，应该从更加广阔的角度来识别自然结构的正确与否。“错误”在词典上的解释是：不正确，与客观实际不符合。若我们以词典上“错误”的解释作为依据，则需要更加明确客观实际在数学中的意义。小学数学的内容可根据客观性、主观性分为这三种：

（1）数学发展规律所形成的：类似的有加法交换律，它实质就是加法运算的自然规律。这种规律不会以人的意志为改变，是客观存在的。

（2）根据数学发展人为规定的：类似的除法中，余数小于除数。虽然这并非除法运算的自然规律，但这样规定可以保证结果的唯一性。举个例子“7÷2”，整数范围内有这样四种结果（如下表），但这几种结果根据乘法公式来检验都是正确的。

被除数与除数分别相等的运算，却是不同的结果，像这种不确定性会让数学推理变得更加复杂。在数学学习中这种形式的推理还是很常见的：

但如果没有规定余数小于除数，那我们也就无法进行进一步的推理了，所以说做此规定是为了运算结果的准确性，这样的规定也同时促进了数学逻辑的发展。

（3）根据某种需求或认为习惯：就好比竖式计算，人们在没有计算机的时候，为了计算更简便，想出来过很多的方法，但最终被流传下来的标准算法，不只是体现了数学规律，更重要的是人为规定的，为了更加简便。再比如概念命名，这也是人为规定的。“质数”这个概念最初被称为“数根”，之后才变为素数或质数。就如同上述所说的结果应写于等号的右边，这也只是人们的习惯而已，不是判断正确与否的依据。

我们若将第一种称作“规律性知识”，二三两种称作“规则性知识”，可以这样说规律性知识客观性更强，规则性知识主观性更强。不能仅仅将主观性作为判断正确与否的依据，更应该将规律性知识作为判断的依据。我们应该鼓励、指引并保护学生不被条条框框限定思维。

四、结语

学生在自然结构下经常会有错误，这也无法避免。所以在教学中，要及时发现这些错误，让学生加深探究，自然而言地将自然结构转化为加工结构。我们要理解学生所犯的错误都有一定的道理性，学生之所以会犯这种错误，与数学规律和对规律的理解这两方面有关，教师在课堂上就是要对这种道理性进行探究。我们可以从以下几个方面来探讨：

（1）收集并整理学生所犯的错误案例，比如课后作业、课堂练习、课堂发言以及考试中出现的错误。

（2）判断收集过来的案例是否为真的错误，判断的依据是看违背的是客观规律或者是主观规则，而辨别的标准主要看其违背的是客观规律还是主观规则。

（3）对错误的原因进行分析。这是最重要的，我们可以从学生的自然结构来分析。

（4）开展具有针对性的教学活动，这种教学活动的重点应该是将自然结构转化到加工结构上去。

上面几点的前三个方面是判断的条件，第四个方面是解决的方法，只有有了判断的依据，才能够提出合理的解决办法。只有这样的课堂才能让学生更好地将自然结构转化为加工结构，课堂效率才会更高。

作者简介：王党英（1965-），小学高级教师，从事小学数学教学工作36年。