“三步+图象”解决传送带运动问题
河北
传送带在日常生产和生活中有着广泛的应用,在车站、机场、工厂等随处可见,有关传送带问题的考题更是频繁出现在高中生的各类考卷中,考查学生的科学素养和实践应用能力。有关传送带问题也一直是高中物理学习中的一个难点问题,很多同学在解决有关传送带问题时比较“犯怵”,其难点在于物体与传送带间运动的牵制,会产生摩擦力的突变,比如静摩擦力消失,滑动摩擦力突然变为静摩擦力,静摩擦力突然变为滑动摩擦力,滑动摩擦力的方向突然改变等等,致使学生在解决问题中出现错误。其实,无论多么复杂的传送带问题,如果分析清楚以下三个问题,以图象辅助分析,都能轻松地得以解决。
第一步:“受力分析求加速度”,即根据物体与传送带的运动情况进行受力分析,求物体的加速度;
第二步:“何时、到哪儿两等速”,即分析多长时间,物体走了多少位移与传送带速度相等;
第三步:“等速后能否共速”,即根据具体条件分析,物体与传送带速度相等后能不能以相同的速度一起运动,当物体与传送带速度相等时往往会发生摩擦力种类、大小及方向的突变。
如果按以上思路分析并回答了上述问题,再结合牛顿运动定律及运动学公式、动能定理等物理规律,以运动图象为辅助分析运动过程,传送带问题便不是什么难题,下面以常见的问题类型分别举例分析。
一、水平传送带上的力与运动情况分析
【例1】水平传送带被广泛地应用于车站、码头、工厂、车间。如图1所示为水平传送带装置示意图,绷紧的传送带AB始终保持v0=2 m/s的恒定速率运行,一质量为m的工件无初速度地放在A处,传送带对工件的滑动摩擦力使工件开始做匀加速直线运动,设工件与传送带间的动摩擦因数为μ=0.2,AB之间的距离为L=10 m,g取10 m/s2。求工件从A处运动到B处所用的时间。

图1
【解析】(第一步,先对工件进行受力分析,求加速度)
工件刚放到传送带上时μmg=ma
代入数据可得a=2 m/s2
(第二步,计算速度相等时所用时间和位移)
设加速过程对应的时间为t1,位移为l
代入数据可得t1=1 s
代入数据可得l=1 m
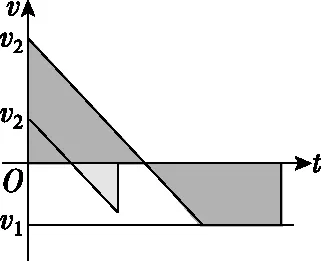
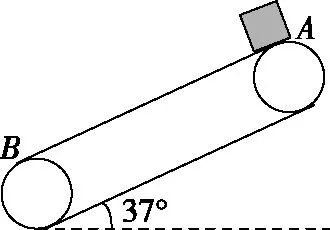
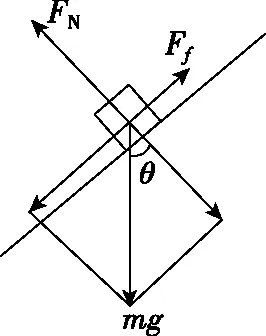
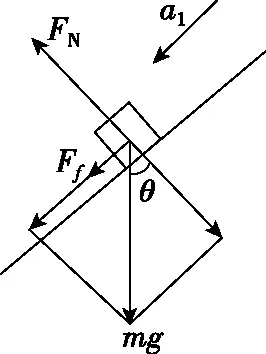
由于l (第三步,分析等速后能否与传送带一起运动,本问题中工件与传送带速度相等后摩擦力消失) 设工件随传送带匀速运动的时间为t2,则 所以工件从A处运动到B处的总时间 t=t1+t2=5.5 s 【反思归纳】这是一道传送带以恒定速度运转,而被运送的工件初速度为0的实际问题,解决这类问题首先要对被运送的工件进行受力分析,一般情况下,工件在传送带上有两种运动形式,一是匀加速运动,二是匀速运动。从匀加速运动到匀速运动过程中,往往要对工件在传送带上做加速运动结束时是否滑离传送带做出判断,如果已经滑离传送带,则工件不存在匀速运动阶段,如果没有滑离,则工件将与传送带一起做匀速运动,可见工件是否滑离传送带的判断是不能忽视的。 【例2】如图2所示为车站使用的水平传送带模型,传送带长L=8 m,以速度v=2 m/s沿顺时针方向匀速转动,有一旅客将一个质量为m=4 kg的行李箱以v0=8 m/s的初速度水平滑上传送带。已知行李箱与皮带间的动摩擦因数为μ=0.5,则行李箱从传送带的A端到B端所需要的时间是多少,在滑动过程中摩擦产生的热量为多少?(g=10 m/s2,且可将行李箱视为质点。) 图2 图3 【解析】(第一步,对行李箱进行受力分析,求加速度。行李箱受力情况如图3所示,行李箱受到自身重力mg,传送带给予的支持力FN,传送带对行李箱的滑动摩擦力Ff方向水平向左) 由牛顿第二定律得μmg=ma 解得a=5 m/s2,方向向左,做减速运动 (第二步,计算行李箱与传送带速度相等时所用时间和位移) 设行李箱在传送带上做匀减速运动的时间为t1,则 代入数据得t1=1.2 s 此时行李箱通过的位移为x1,由匀减速运动的规律得 解得x1=6 m 可知在匀减速运动阶段,行李箱没有滑离传送带。 (第三步,分析等速后能否与传送带一起运动,本问题中行李箱与传送带速度相等后摩擦力消失) 代入数据可得t2=1 s 故行李箱在传送带上运动的时间为t=t1+t2=2.2 s 两个物体因摩擦产生的热量等于两者间的摩擦力与相对路程的乘积 相对路程Δs=x1-vt1 产热为Q=μmg·Δs 代入数据得Q=72 J 【反思归纳】例2与例1最大的区别是被运送物体的初速度比传送带运动的速度要大得多,这一题设条件的变化,直接影响到工件在传送带上所受滑动摩擦力的方向,此时摩擦力所起到的作用不是使例1中物体加速,而是使物体减速。显而易见初始运动情况会影响受力情况,进而影响后来的运动情况,注意计算产生热量为摩擦力与相对路程的乘积。 【例3】如图4所示,一足够长的水平传送带以恒定的速度v1沿顺时针方向转动,传送带右端有一与传送带等高的光滑平台,一小物块以恒定速度v2沿直线向左滑上传送带后,经过一段时间又返回光滑平台,返回时物块的速率为v2′,则下列关于返回物块速率的说法正确的是 ( ) 图4 A.只有v1=v2时,才有v2′=v1 B.若v1>v2时,则v2′=v2 C.若v1 D.不管v2多大,v2′=v2 【解析】第一步,对物体进行受力分析,求加速度。本题中物体速度与传送带速度方向相反,受到摩擦力向右,可知物体先向左减速运动,减速到0后向右做匀加速直线运动,整个过程中,加速度不变。 第二步,计算物体与传送带速度相等时所用时间和位移。本题中没有确定给出物块与传送带间的动摩擦因数以及两者的速度关系,用图象法进行半定量分析会使问题变得更为简单,如图5所示,设速度方向向左为正方向,图象中速度与时间轴所夹的面积上下两部分相等时返回出发点。 图5 第三步,分析等速后能否与传送带一起运动,本问题中小物块与传送带速度相等后摩擦力消失,由图象可以看出,当v1>v2时,还没有达到与传送带速度相等就已经返回了,而当v1 综上分析,本题答案为B。 【反思归纳】按以上三步分析清楚物理过程,在此基础上,结合图象便可很容易得出正确答案。本题以“力和运动的关系”知识为载体,着眼于考查学生的理解能力、推理能力、综合分析能力、建立理想模型来解决实际问题的能力,能很好地考查考生的物理核心素养。 【例4】如图6所示,一传送带倾斜放置与水平方向夹37°角,两端点AB距离为L=16 m,传送带以恒定速度v=10 m/s运动,在传送带上端A处无初速释放质量为m=0.5 kg的物块,物块与带面间的动摩擦因数μ=0.5,求: 图6 (1)当传送带顺时针转动时,物块从A到B所经历的时间为多少? (2)当传送带逆时针转动时,物块从A到B所经历的时间为多少?(sin37°=0.6,cos37°=0.8,取g=10 m/s2) 【解析】(1)(第一步,对物块进行受力分析,求加速度。当传送带顺时针转动时,传送带相对物块向上运动,所以传送带受到物块的摩擦力沿传送带向下,物块受传送带的摩擦力方向向上,如图7所示,由于mgsin37°>μmgcos37°,故物块向下作初速度为0的匀加速运动直到B处。不存在分析第二、三步) 图7 根据牛顿第二定律得 mgsin37°-μmgcos37°=ma 代入数据可得a=2 m/s2 物块在传送带上做加速度为a=2 m/s2的匀加速运动,设运动时间为t,则 代入数据可得t=4 s (2)(第一步,对物块进行受力分析,求加速度) 物块放上传送带的开始的一段时间受力情况如图8所示,刚放物块时受摩擦力方向沿斜面向下,设加速度为a1,由牛顿第二定律得 图8 mgsin37°+μmgcos37°=ma1 解得a1=10 m/s2,作初速为0的匀加速运动。 (第二步,计算物块与传送带速度相等时所用时间和位移) 设物块加速时间为t1,则 解得t1=1 s (第三步,分析等速后能否与传送带一起运动) 速度相等后物块便与传送带产生向下运动趋势,比较mgsin37°与μmgcos37°发现物体不能与传送带相对静止,将沿传送带加速下滑。 设速度相等后物块的加速度为a2,其受力情况如图9所示。由牛顿第二定律可知 图9 mgsin37°-μmgcos37°=ma2 解得a2=2 m/s2 设后一阶段物块下滑到底端所用的时间为t2可得 解得t2=1 s 所以物块从A到B的时间为 t=t1+t2=2 s 【反思归纳】解答本题的关键是分析摩擦力的方向,以及摩擦力向上和向下的条件。审题时应注意对已知条件作必要的定性分析和半定量的分析。如由本题中给出的μ和θ值可作出以下判断:当μ≥tanθ时,物块在加速至与传送带速度相同后,物块将与传送带相对静止,并同传送带一起匀速运动;当μ 【例5】仓库中常用的皮带传输装置示意图如图10所示,它由两台皮带传送机组成,一台水平传送,A、B两端相距3 m,另一台倾斜,传送带与地面的倾角为θ=37°,C、D两端相距4.45 m,B、C相距很近。水平传送以5 m/s的速度沿顺时针方向转动,现将质量为10 kg的一袋大米无初速度地放在A端,它随传送带到达B端后,速度大小不变地传到倾斜送带的C点,米袋与两传送带间的动摩擦因数均为0.5。(本题中g取10 m/s2,sin37°=0.6,cos37°=0.8) 图10 (1)若CD部分传送带不运转,求米袋沿传送带在CD上所能上升的最大距离; (2)若倾斜部分CD以4 m/s的速率顺时针方向转动,求米袋从C运动到D所用的时间。 【解析】(1)(第一步,对物块进行受力分析,求加速度) (第二步,计算米袋与传送带速度相等时所用时间和位移) (第三步,分析等速后能否与传送带一起运动) 米袋加速一段后与传送带一起匀速运动到达B点,到达C点时速度v0=5 m/s 到达CD段后,设米袋在CD上运动的加速度大小为a 由牛顿第二定律得mgsinθ+μmgcosθ=ma 代入数据得a=10 m/s2 (2)倾斜部分传送带沿顺时针方向转动时,继续考虑分析相关的三个问题来解决问题。 (第一步,对物块进行受力分析,求加速度) 米袋速度减为4 m/s之前的加速度为 a1=-g(sinθ+μcosθ)=-10 m/s2 (第二步,计算米袋与传送带速度相等时所用时间和位移,本题中只考虑位移) (第三步,分析等速后能否与传送带一起运动) 米袋速度等于4 m/s时,滑动摩擦力方向改变,由于μmgcosa a2=-g(sinθ-μcosθ)=-2 m/s2 可见,米袋速度减速到0时,恰好运行到D点 米袋从C运动到D所用的时间t=t1+t2=2.1 s。 【反思归纳】解答此题的关键是准确分析物块在水平和倾斜传送带上的受力情况,并据此分析出物块在两种状态的传送带上的运动情况。在具体的分析过程中应该注意物块在水平和倾斜传送带上受力和运动情况的特点来分析,可以很好的考查学生对力和运动的物理观念。

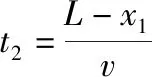

二、倾斜传送带上的力与运动情况分析


三、水平和倾斜组合传送带上的力与运动情况分析

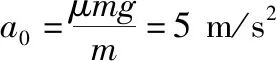
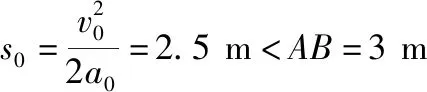

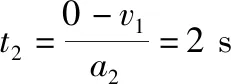

——“模型类”相关试题选登

