导弹制导精度估计方法研究及其应用*

马金龙 马立元 方 丹

（陆军工程大学石家庄校区导弹工程系 石家庄 050003）

1 引言

导弹的制导精度是一个非常重要的性能参数，它是对武器作战效能最直接的体现。其制导精度越高，精确打击目标的能力也就越强［1］。在获取导弹与目标遭遇时的落点信息后，对数据的处理方法主要包括经典统计方法和Bayes统计方法。伴随着计算机技术和信息贮存技术的发展，使得测试之前就有了大量的试验数据，传统的经典统计方法已经不能满足工程实际中的要求。因此，为充分利用这些有效信息，提高制导精度估计的准确度和可信度，需要一种新的统计方法，Bayes统计方法恰好适应了这种要求［2］。Bayes统计方法可有效利用大量的验前数据，并随着试验数据的增加不断修正估计值，提高估计的可信度。20世纪90年代中期以来，无论在理论研究还是在应用方法上，Bayes统计都取得了比经典统计更快的发展，在工程技术领域，Bayes统计越来越受到关注，已经成功应用于可靠性分析［3］、精度分析［4］、多传感器融合［5］、神经网络计算［6］等领域中。尤其在武器装备的精度鉴定中，Bayes试验统计方法受到了极高的重视，通过运用各种信息，减少现场试验次数，缩短武器系统研制周期，节省费用，早日定型和装备部队。

本文基于仿真的测试环境下，提出了一种加权条件下的动态Bayes估计方法，并基于相关函数的融合方法合理确定验前信息的权重。既可以快速计算出导弹仿真的落点样本信息的均值和方差的估计值，又可随仿真信息的增加不断对结果进行修正，提高导弹制导精度估计的精度。

2 基于仿真环境的制导武器制导精度估计方案

导弹的试验鉴定一般通过大量的外场试验来达到鉴定武器系统性能的目的，由于武器造价越来越昂贵，靶试费用也高，大量的靶试会造成增加较高的成本［7］。随着半实物仿真技术的发展，半实物仿真试验的可信度也越来越高。半实物系统仿真试验为各个型号导弹的研制做出很大的贡献，不仅极大缩短研制的周期，而且还节约了大量的研制经费。20世纪60年代以来，美国在爱国者导弹、尾刺导弹、以及响尾蛇空空导弹等武器的研制过程中大量的运用半实物实时仿真技术，大幅降低了打靶量，产生了巨大的经济效益。我国的半实物实时仿真技术起步较晚，基于半实物实时仿真环境的条件下，如何有效利用仿真信息评估导弹的制导精度，目前也还没有成熟的方法和相关评估鉴定标准。本文基于Bayes统计的方法，针对导弹精度评估问题的Bayes估计方案如图1。

图1 精度鉴定方案图

仿真条件下对导弹制导精度估计的具体步骤为

1）：根据数据的来源分类整理所获得的验前信息，通常分为数学仿真数据和不同阶段的半实物实时仿真数据（如仅惯组在回路，惯组、弹上机在回路，惯组、弹上机、舵机在回路）；

3.1.1 均值的动态估计

3）采用基于相关函数的信息融合方法计算各组仿真数据的权值；

4）根据加权条件下的Bayes估计公式得到仿真数据均值和方差的估计值，评估导弹的制导精度。

为探索钻井废弃泥浆用于路基路面材料可行性，取了5口井的样品，并对其主要污染指标进行了分析，分析结果见表1。5个钻井废泥浆样品，其主要污染情况不同，其中样品1号，污染指标主要是色度、COD超标；其他四个样品除了色度、COD超标外，重金属六价铬也超标。5个样品中样品3号污染最严重，处理难度更大一些。因此，选择3号样品作为试验对象。

3 加权条件下的Bayes估计方法研究

当只有两组样本数据时，可得μ^的Bayes估计公式：

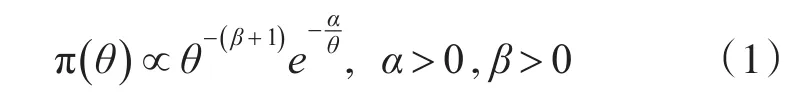
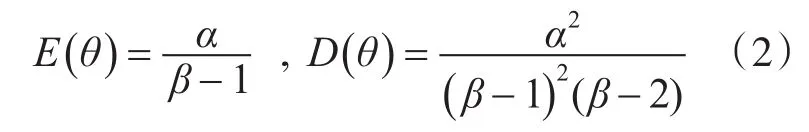
用矩法对IGamma分布中的参数α和β进行估计，求得：

在路基加宽的过程中，由于旧路基经过长时间使用，已经被车辆基本压实，而新路基施工之后的一段时间之内，受到材料与荷载因素的影响，会出现沉降现象，这就导致新旧路基之间的衔接面相互脱离，不能保证加宽施工质量符合要求，严重影响公路路基加宽施工结构的使用强度，对其使用寿命造成危害。

三是找到科学的公允会计计量途径。即根据金融市场运行的规律建立起公允会计计量的多元化的定价模型和测试方法，特别是要在公允会计计量规范下科学地比较不同定价模型和测试方法的优劣；在公允会计计量规范下对不同产品进行数量、品种、市场价格和长短期限等方面进行价值对比，建立健全与金融工具定价有关的公司治理和内控制度，并提高信息披露的透明度等[17]。在公允会计计量规范下针对金融监管给金融市场带来的顺周期性进行科学规范，这是金融市场健康发展的重要路径。

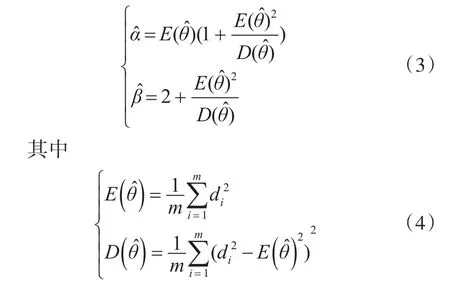
E()和D()为正态分布(μ，D)总体的充分统计量。

使用Cadence virtuoso等软件,采用0.35 μm CMOS工艺对128×128阵列、2×2单元输入完成了版图设计和DRC、LVS验证[13],其中128×128阵列读出电路的版图如图7所示,2×2单元输入的版图如图8所示。

3.1 加权条件下导弹落点信息均值和方差的动态Bayes估计模型

设制导武器落点数据X服从正态分布，验前有一样本数据X1，现场又获得一组样本值X2，基于Bayes估计方法估计其分布参数，，表达式为

其中n1、n2为样本量，和为各自样本均值，α，β为Bayes融合估计后的IGamma分布参数。得到和的估计值，就可以计算CEP和制导精度的Bayes估计。

本研究以2001-2010年河南省农业生态经济系统中能量投入数据为基础，部分农业生产投入产出按照能量折算规则换算成能量状态，再将计算得来的数据乘以相应的太阳能值转换率得到其能值数值。农业生产投入按照可更新环境资源R、不可更新环境资源N、不可更新工业辅助能F和可更新有机能T4项投入分类编制，形成2001-2010年河南省农业生产生态经济系统能值投入表，如表1所示。

加权先验分布给出了一个合理利用历史数据来计算现场数据之前的参数的先验分布的方法，避免了完全不利用验前信息或盲目利用验前信息的不合理的处理方法［9］。数学仿真数据和不同模式下的半实物仿真数据的先验权值不同，不能简单地合并数学仿真数据和半实物仿真数据，而应建立相应的加权先验方案，给每个不同阶段所得历史数据一个合理的权参数。随着武器装备研制方案的不断改进，武器试验鉴定数据也会不断更新和增加，因此弹点散布方差的估计也是一个动态时变的过程。既然每次的弹点散布方差的后验分布都是当前对样本总体的一个更为接近实际情况的近似估计，那么也可以作为下一次估计的先验分布。因此对于参数和的动态估计的研究就显得十分有意义。这里设试验鉴定前的样本数据为X1，X2，X3……Xm，样本量为n1，n2，n3……nm。

2）分别计算出各组数据的先验Bayes估计值；

Bayes统计中，选取恰当的先验分布是正确反映先验信息和进行进一步统计推断的前提和基础［8］。制导武器的落点信息X（d1，d2…dm），其数据均为一维空间中弹点到靶心的距离，或者为二维指数距离，在落点服从正态分布N(μ，D)的假设下，记θ=(μ，D)的验前分布为IGamma分布，则其验后分布仍为IGamma分布。记为θ～IG(α，β)，则：

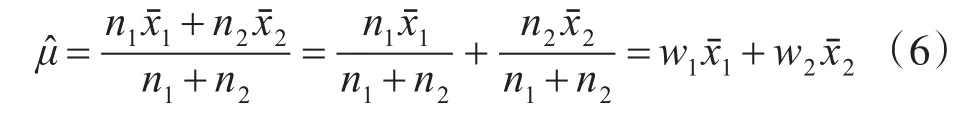
预应力技术在桥梁公路作业中的应用，已有较长时间，但我国在这方面起步晚，技术发展仍有较大的进步空间，在实际操作施工过程中也没有明确规范步骤，因此，施工要求标准较低，施工不严格，在通常情况下，很多施工单位采取的方法都是采用1.5级的油压表作为施工计量工具，但是在实际施工过程中，由于施工技术人员的素质水平较低，没有控制好张拉幅度，使最终得出的数值与实际需要的数值相差甚远，而且由于张拉力在不同阶段出现较大差异，因此导致混凝土环境整体下降，结构强度较低。所以，在张拉力控制方面，需要不断明确操作规范，提高攻克技术难题的能力，不断提升设备的质量。

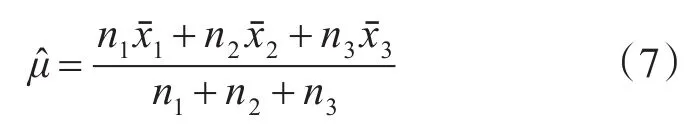
推广可得，对于试验鉴定前的样本数据为X1，X2，X3……Xm，其样本量为n1，n2，n3……nm，参数的Bayes动态估计公式为

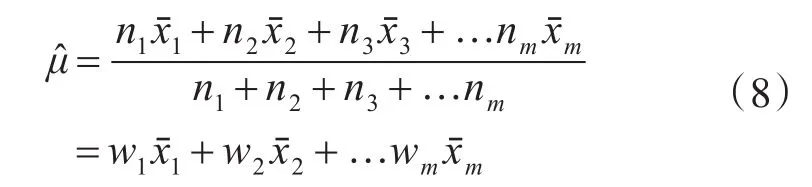
目前美国、欧盟、加拿大、中国等国家针对手性药物都颁布了相应地指导原则，但不同国家对于手性药物以及开发单一异构体药物的监管要求存在差异［16，23‐24］。下面就具有代表性的几个国家颁布的指导原则进行总结和比较。

总而言之，在农业发展中，土肥管理技术对农业经济作物的产量和质量有着重要的作用。在玉米的土肥管理中，要做好耕种前的准备工作，进行扒土蹲苗，同时做好中期除草、培土，后期浅中耕和免耕直播。在做好土壤耕种时要进行施肥管理，根据玉米生长过程中出现的具体问题进行具体分析，采取相应的措施。在玉米的土肥管理中，可以借助科学技术对玉米生长情况进行管理，提高玉米土肥管理的智能化和数字化，保障玉米的健康成长，提高玉米的产量和质量。

假设各阶段的样本数据的权值为εi，其中1≤i≤m，其加权条件下的重要程度为εini，则加权条件下的均值Bayes估计公式为

3.1.2 样本方差的Bayes动态估计模型

本文基于相关函数的融合方法，在确定各信息源权重的过程中，充分考虑单一验后分布与融合验后分布的相关程度［10］。根据这种相关程度设置的的权值是合理的。即单一的验后分布越接近融合验后分布，则该数据权值越大［11］。

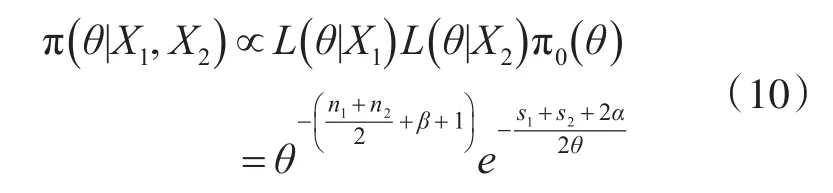
如此递推当获得第m阶段的数据时，参数θ的后验分布为

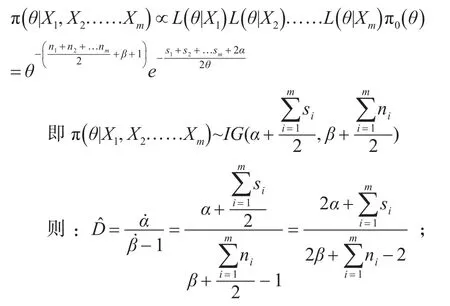
其中α，β由第一阶段的样本数据求得。

假设各阶段的样本数据的权值为εi，其中1≤i≤m，其加权条件下的重要程度为εini，则加权条件下的方差的Bayes估计公式为

其中σ2=，1≤ ≤m；

3.2 各阶段数据权值的计算

由样本方差的估计公式可知，对样本方差的估计就是对参数θ的估计。θ的初始先验分布为π(θ)～IG(α，β)，则融合后验分布依然为 IGamma分布。当获得前两阶段的样本数据X1，X2时，参数θ的后验分布为

IGamma分布的数学期望和方差分别是：

根据均值Bayes估计公式可知，样本数据对Bayes估计的结果的贡献只与样本数据量n有关，因此在未加权的情况下，样本数据量越大，其重要程度也就越多。通过给样本数据加权，使其对估计结果的影响程度更加合理，使我们得到的Bayes估计值更加合理。加权的本质就是变相的改变样本数据量从而改变样本数据对结果的影响程度。

由此我们可以清楚地看到，王钻清在诗歌写作中，并非像某些诗歌写作者那样，仅仅是满足于卡拉OK似的自娱自乐，而是有着更加开阔的诗歌艺术境界和宏伟的写作抱负。王钻清是一个博览群书，对于中国传统文化有着深厚学养的学者型和性情诗人。在诗歌写作中，他不屑于表现那种个人的小情趣和井蛙之见，而常常将目光转到整个的人类和古老的历史，正是因为有了这样密切关乎人类命运和心灵的哲学思考，我们在阅读王钻清的诗歌时，才能够深深地感受到那种与众不同，直击人心，撼人心魄的艺术力量。

假设系统有n个输入k，一个输出y，设yi为系统第i次的实验结果，y为全因素试验的输出结果，由回归分析，求得yi和i的解析式：

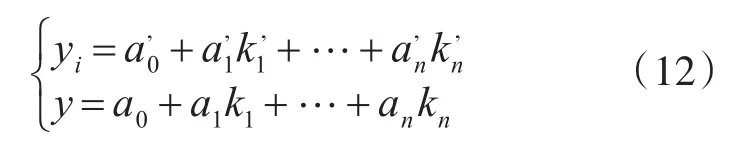
其中，ki为影响yi的因素，ai和为回归系数，1≤i≤n。

定义个体相关系数为

其中，i=1，2…n，为随机变量yi的方差，且0≤γyiy≤1。

试验鉴定中导弹落点精度的估计，分别需要综合数学仿真数据、半实物仿真数据和飞行试验数据。设X1为数学仿真数据，X2为半实物仿真试验数据，X为现场半实物试验数据，Θ为待估计的未知参数。 π1(θ)为X1的融合验前分布，π2(θ)为X2的融合验前分布［2］。则融合验前分布：

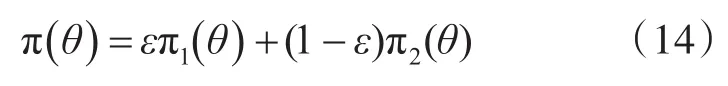
其中，ε为需要利用相关函数法确定的权重系数。其计算步骤为

目前澳大利亚事故车维修领域的学徒工数量不容乐观，而且退出率依然不低。一些行业机构也在开展一些提升项目，将行业培训引入到学校中，以加快学徒工培养过程，同时确保学徒人员通过培训得到技术指导和支持。2017年澳大利业取消了457签证项目，这使得车身维修行业更难引入外国工人。喷漆人员已经从熟练技术移民的名单中去除，这表明政府并不认为国家缺少这方面人才，但目前，恢复车身维修方面技术移民的呼声已经在业内响起。

1）由验前分布 π1(θ)的期望μ1，验前分布 π2(θ)的期望μ2；分别结合现场数据X，通过贝叶斯公式可得到验后分布的分布参数，期望值分别为，方差值为；令

由于方程组中有三个未知数，所以需要通过在样本验前分布中分别随机抽样三组数据，用每一组的样本均值代替各自的总体均值，就可以求解该方程，得到明确的解析式［3］。

2）验前数据权值的确定

党的十九大召开后，意识形态工作已经纳入了新时代党的建设总要求，职业院校党委要旗帜鲜明讲政治，牢牢把握意识形态工作的领导权和主导权，切实担负意识形态工作的主体责任。建立健全党委统一领导、党政工团齐抓共管、党委宣传部门牵头协调、有关部门和各院(系)共同参与和齐抓共管的意识形态工作新格局，形成抓长抓制度落实、抓常抓职责履行、抓细抓工作督查的新常态工作机制，切实将意识形态纳入全面从严治党责任清单，责任到人，加强考核，开创意识形态工作新局面。

根据相关系数可得：

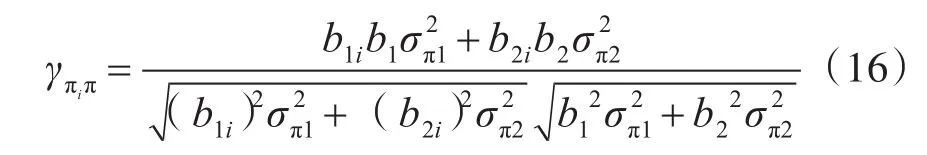
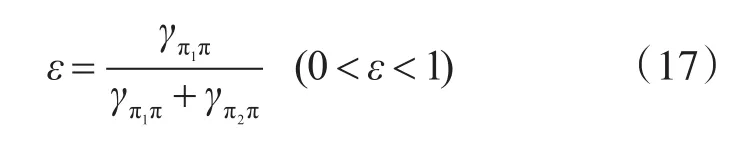
4 动态Bayes估计算法在制导武器制导精度估计中的应用

导弹仿真的落点样本信息 X（d1，d2…dm），其数据均为一维空间中弹点到靶心的距离，或者为二维指数距离，其落点数据服从正态分布。假设有两组仿真数据，X1为数学仿真数据，其先验均值μ1=0.2 ，方差σ12=0.1，X2为数学仿真数据，其先验均值μ2=0.4，方差σ22=0.2，样本数据量均为10，其中半实物仿真数据最接近于真实值。基于相关函数方法计算所得数学仿真数据的权值ε=0.75。此时的动态Bayes估计公式为

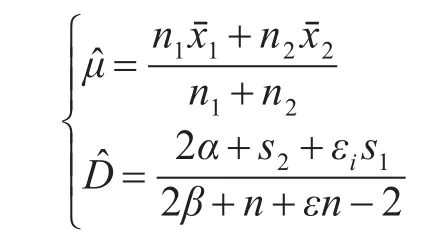
其中α，β根据第三节式（3）求得：

由于半实物仿真数据结果更接近与导弹的实际飞行状态，通常情况下我们认为半实物仿真有着更高的可信度。根据计算所得结果可知，加权条件下的均值和方差值更接近于半实物仿真数据的先验Bayes估计值，因此可以认为加权条件下的Bayes估计结果明显要优于未加权的结果，同时也避免了仅利用半实物仿真数据而完全不考虑数学仿真数据的结果。并且基于相关函数计算所得的数学仿真数据的权值最大为1，即其重要程度最多等同于半实物仿真数据，保证了其可信度不会超过半实物仿真数据，也说明权值的计算方法是合理的。有了落点信息均值和方差的估计，便可对导弹制导精度进行评估。

根据回归方程计算方程自变量对因变量之差的绝对值小于20%时因变量的定义域范围。令0.8Y＜ X＜ 1.2Y，则 0.045＜ X＜ 1.37；0.8Y＜ Z＜1.2Y，则0.162＜Z＜0.494。

5 结语

基于仿真环境的导弹试验鉴定技术在近几年越来越受到重视，研究仿真试验数据的处理方法也亟待有完善的评估标准。本文基于半实物仿真试验数据为载体，研究了加权条件下的Bayes估计方法及其在导弹制导精度中的应用。结果证明加权条件下的Bayes估计方法更加科学可靠，可充分利用试验鉴定前的各种仿真数据，为实际飞行鉴定试验提供参考，便于实际中的工程应用。